พีชคณิตเวกเตอร์ (Vectors algebra)
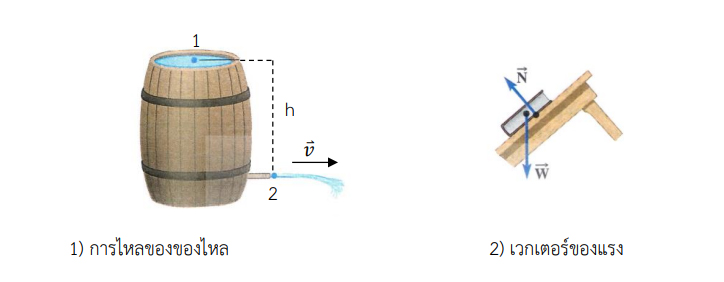
ในทางฟิสิกส์และวิศวกรรมศาสตร์นั้นการทราบจำนวนและหน่วยของปริมาณใดปริมาณหนึ่งจะไม่เพียงพอสำหรับอธิบายปริมาณนั้น ๆ ให้สมบูรณ์ได้ เช่น การเดินไปทางทิศเหนือ 8 กิโลเมตร ย่อมมีตำแหน่งแตกต่างจากการเดินไปทางทิศตะวันออก 6 กิโลเมตร การกล่าวเพียงสั้น ๆ ว่าได้เดินทางไป 8 กิโลเมตร จะไม่สามารถบอกตำแหน่งสุดท้ายได้ถ้าไม่ทราบทิศของการเดิน ตำแหน่งที่เปลี่ยนไปนี้เราเรียกว่า การกระจัด (Displacement) ซึ่งเรียกปริมาณที่มีทั้งขนาด (Magnitude) และทิศทาง (Direction) ว่า ปริมาณเวกเตอร์ (Vector quantity) เช่น ความเร็ว ความเร่ง แรง โมเมนต์ ฯลฯ ส่วนปริมาณที่มีเฉพาะขนาดเพียงอย่างเดียวจะเรียกว่า ปริมาณสเกลาร์ (Scalar quantity) เช่น มวล ปริมาตร ความหนาแน่น ความดัน อุณหภูมิ อัตราเร็ว อัตราเร่ง ฯลฯ การคำนวณทางคณิตศาสตร์ของปริมาณสเกลาร์ จะเหมือนกับการคำนวณทั่วไป ส่วนการคำนวณปริมาณเวกเตอร์ จะต้องคำนึ่งถึงทิศทางของปริมาณนั้นด้วย จึงเรียกการคำนวณแบบนี้ว่า พีชคณิตเวกเตอร์ (Vector algebra) ซึ่งจะกล่าวอย่าง ละเอียดดังต่อไปนี้
1.1.1 ปริมาณสเกลาร์ (Scalar quantity) ปริมาณสเกลาร์ คือ ปริมาณที่มีแต่ขนาดเพียงอย่างเดียว ไม่มีทิศทาง ตัวอย่าง เช่น เวลา อุณหภูมิประจุไฟฟ้า พลังงาน และปริมาตร มวล ระยะทาง อัตราเร็ว อัตราเร่ง เป็นต้น ดังนั้นปริมาณสเกลาร์จึงเป็นปริมาณต่าง ๆ ที่บอกแต่เพียงขนาดเพียงอย่างเดียวก็เป็นที่เข้าใจได้อย่างสมบูรณ์ได้
1.1.2 ปริมาณเวกเตอร์ (Vector quantity) ปริมาณเวกเตอร์ คือ ปริมาณที่มีทั้งขนาดและทิศทาง ซึ่งอาจเขียนแทนด้วยลูกศร โดยความยาวลูกศรจะแสดงขนาดและหัวลูกศรแสดงทิศทางของเวกเตอร์นั้น ๆ นอกจากนี้เรายังสามารถเขียนเวกเตอร์ได้ โดยการกำหนดขนาดเวกเตอร์ด้วยตัวอักษรโรมันที่มีหัวลูกศรกำกับ
หรือเขียนเป็นตัวตัวหนา (ตัวทึบ) ก็ได้ ดังเช่นรูปที่ 1-6 ( ในเอกสารนี้จะใช้สัญลักษณ์ A แทนเวกเตอร์ 𝐴⃑ หรือ 𝐵 แทนเวกเตอร์ 𝐵⃑ )
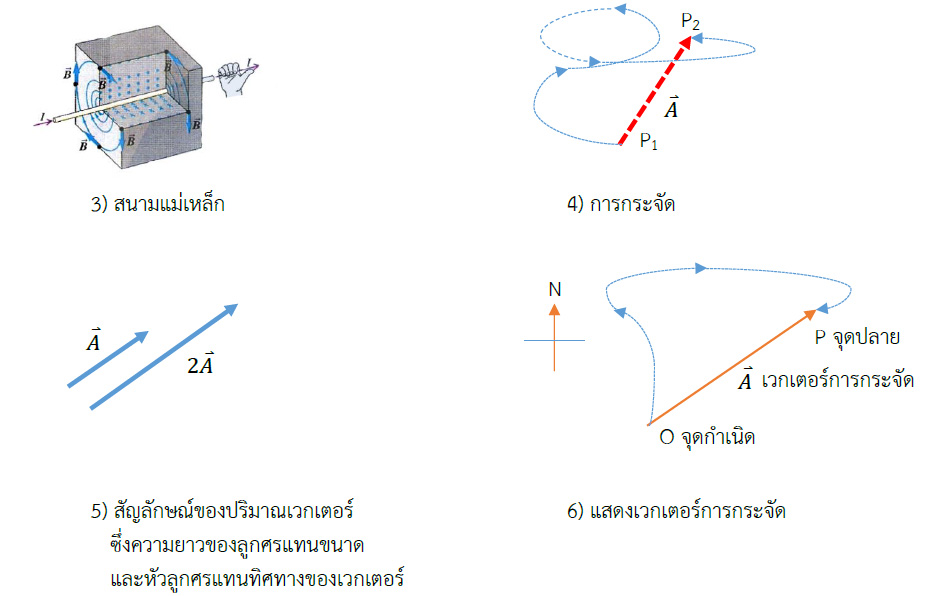
ในรูปที่ 6 ถ้าเวกเตอร์ 𝐴⃑ แทนการกระจัดขนาด 6 km จากจุด O ไปยังจุด P ใน ทิศตะวันออกเฉียงเหนือ
จุดเริ่มต้น O คือหางลูกศร เรียกว่าจุดกําเนิดของเวกเตอร์ ส่วน P คือจุดหัวลูกศร เป็นจุดปลายของเวกเตอร์ ดังนั้นเขียนเวกเตอร์ 𝐴⃑ แทนด้วย OP ได้ คือการลากเส้นจาก จุดเริ่มต้น O ไปจุดปลาย P โดยมีลูกศรกํากับไว้ที่ปลายเส้น
ขนาดของเวกเตอร์𝐴⃑ เขียนเป็นค่าสมบูรณ์𝐴⃑ = |𝐴⃑|= 6 km หรืออักษรโรมัน ตัวปกติ A ซึ่งเป็นอักษรตัวเดียวกัน
นั้นเอง ในการเขียนสัญลักษณ์แทนปริมาณเวกเตอร์ด้วยลายมือ หรือพิมพ์ดีดต้องมีลูกศรกํากับไว้ด้วยเสมอ ส่วนใน
เอกสารนั้นจะใช้สัญลักษณ์เป็นอักษรโรมันตัวหนาแทนเวกเตอร์
1.1.3 องค์ประกอบเวกเตอร์ (Vector component)
ในระบบพิกัดฉากของระนาบ xy ถ้ากําหนดเวกเตอร์ 𝐴⃑ ทํามุม กับแนวแกน x ดังรูปที่ 7
องค์ประกอบของเวกเตอร์ 𝐴⃑ตามแนวแกน x คือ 𝐴⃑
𝑥 และแกน y คือ 𝐴⃑
𝑦 ซึ่งสามารถ เขียนให้อยู่ในรูปเวกเตอร์ใน
ระบบแกนพิกัดฉาก ได้ คือ
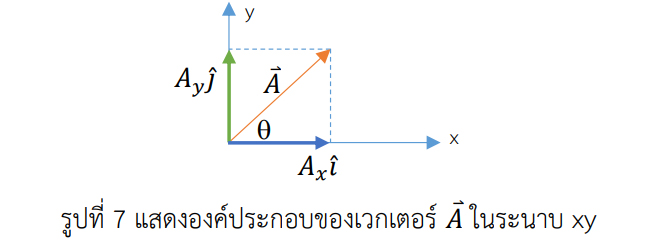
𝐴⃑ = 𝐴⃑
𝑥 + 𝐴⃑
𝑦 = 𝐴𝑥𝑖Ƹ+ 𝐴𝑦𝑗Ƹ (1.1)
เมื่อ 𝑖Ƹและ 𝑗Ƹคือเทอมที่กําหนดเฉพาะเพื่อบ่งบอกทิศทางซึ่งมีขนาดเท่ากับหนึ่
ง และไม่มีหน่วย เรียกว่า
เวกเตอร์หนึ่งหน่วย (Unit vector) ท นั้นตามแนวแกน +x และแกน +y ตามลําดับ (เอกสารนี้จะใช้สัญลักษณ์ของ
เวกเตอร์หน่วยของเวกเตอร์ใด ๆ เป็นพยัญชนะตัวเล็กหนา เช่น เวกเตอร์ 𝐶⃑ มีเวกเตอร์หน่วยคือ 𝑐Ƹ (แต่ตําราบาง
เล่มอาจจะใช้เวกเตอร์หน่วยเป็น 𝑖Ƹ, 𝑗Ƹ, 𝑘̂ หรือ 𝑐Ƹ ก็ได้) ดังนั้น
𝑖Ƹ=𝐴⃑𝑥
𝐴𝑥, 𝑗Ƹ=𝐴⃑𝑦 𝐴𝑦 (1.2)
และขนาดของเวกเตอร์𝐴⃑
𝑥 และ 𝐴⃑
𝑦 พิจารณาจากสมการของตรีโกณมิติมีขนาดเท่ากับ 𝐴⃑
𝑥 = 𝐴 cos 𝜃 , 𝐴⃑
𝑦 = 𝐴 sin 𝜃 (1.3)
ซึ่งองค์ประกอบของเวกเตอร์อาจเป็นบวกหรือลบก็ได้อน
ึ่งการกําหนดแกน x และ แกน y ถ้าเขียนแกน x
หรือแกน y เฉย ๆ จะหมายถึงชี้ไปทางแกนบวก
การตั้งแกนพิกัด (Coordinate) โดยทั่วไปแล้วจะตั้งให้อยู่ในแนวระดับและแนวดิ่ง แต่ในบางกรณี เช่น ใน
กรณีระนาบเอียง ให้ตั้งแกน x ขนานกับระนาบเอียง และแกน y ตั้งให้ตั้งฉากกับระนาบเอียง จะทําให้ง่ายต่อการ
คํานวณ






