พีระมิด กรวย และทรงกลม
3.1 ปริมาตรและพื้นที่ผิวของพีระมิด
3.2 ปริมาตรและพื้นที่ผิวของกรวย
3.3 ปริมาตรและพื้นที่ผิวของทรงกลม
พื้นที่ผิวและปริมาตร
พื้นที่ผิวและปริมาตรของพีระมิด
ทรงสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมซึ่งไม่อยู่บนระนาบเดียวกับฐานและหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกัน เรียกว่า พีระมิด การเรียกชื่อพีระมิด นิยมเรียกชื่อตามลักษณะรูปเหลี่ยมของฐาน ตัวอย่างเช่น พีระมิดฐานสี่เหลี่ยมผืนผ้า พีระมิดฐานหกเหลี่ยม เป็นต้น
พีระมิดแบ่งออกเป็น 2 ลักษณะ คือ พีระมิดตรงและพีระมิดเอียง การจะหาพื้นที่ผิวและปริมาตรของพีระมิดได้นั้น ควรจะหาความยาวด้านต่างๆ ของพีระมิดให้ได้เสียก่อน การหาความยาวด้านต่างๆ มักใช้ทฤษฎีบทปีทาโกรัส
ตัวอย่างที่ 1 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 10 นี้ว ส่วนสูงยาว 12 นิ้ว จงหาความสูงเอียง
วิธีทำ วาดรูปพีระมิดฐานสี่เหลี่ยมจัตุรัสขึ้นมาก่อน
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 10 ÷ 2 = 5 นิ้ว
ตามทฤษฎีปีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = 13
ตอบ สูงเอียงยาว 13 นิ้ว
สูตรพื้นที่ผิวและปริมาตรของพีระมิด
พื้นที่ผิวข้างของพีระมิด พื้นที่ผิวข้างของพีระมิด = ½ × ความยาวรอบฐาน × สูงเอียง
พื้นที่ผิวของพีระมิด พื้นที่ผิวทั้งหมด = พื้นที่ฐาน + พื้นที่ผิวข้างทุกด้าน
ปริมาตรของพีระมิด ปริมาตรของพีระมิด = 1/3 × พื้นที่ฐาน × สูง
ตัวอย่างที่ 2 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 10 นิ้ว ส่วนสูงยาว 12 นิ้ว จงหาพื้นที่ผิวข้างพีระมิด
วิธีทำ เนื่องจาก สูตรพื้นที่ผิวข้างของพีระมิด = ½ ×ความยาวรอบฐาน × สูงเอียง
แต่โจทย์ไม่กำหนดความยาวสูงเอียง ดังนั้น ต้องหาความยาวสูงเอียงก่อน
ขั้นที่ 1 หาสูงเอียง
ให้ AC เป็นส่วนสูง ยาว 12 นิ้ว, และ AB เป็นความสูงเอียง
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 10 ÷ 2 = 5 นิ้ว
ตามทฤษฎีปีทาโกรัสในรูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AB2 = 122 + 52 = 144 + 25 = 169
จะได้ AB = 13
ดังนั้นสูงเอียงยาว 13 นิ้ว
ขั้นที่ 2 หาพื้นที่ผิวข้าง
พื้นที่ผิวข้างของพีระมิด = ½ × ความยาวรอบฐาน ×สูงเอียง
พื้นที่ผิวข้างพีระมิด = ½ × ( 10 + 10 + 10 + 10 ) × 13
= ½ × 40 × 13
= 260 ตารางนิ้ว
ตอบ 260 ตารางนิ้ว
ตัวอย่างที่ 3 จงหาปริมาตรของพีระมิดตรงฐานสี่เหลี่ยมจัตุรัส ที่มีด้านฐานยาวด้านละ 22 เซนติเมตร ส่วนสูง 15 เซนติเมตร
วิธีทำ ปริมาตรของพีระมิด = 1/3 × พื้นที่ฐาน × สูง
ปริมาตรของพีระมิดนี้ = 1/3 × ( ด้าน × ด้าน ) × สูง
= 1/3 × ( 22 × 22 ) × 15
= 22 × 22 × 5
= 2,420 ลูกบาศก์เซนติเมตร
ตอบ 2,420 ลบ.ซม.
พื้นที่ผิวและปริมาตรของปริซึม
ทรงสามมิติที่มีฐานทั้งสองเป็นรูปเหลี่ยมที่เท่ากันทุกประการ ฐานทั้งคู่อยู่ในแนวระนาบที่ขนานกันและด้านข้างแต่ละด้านเป็นรูปสี่เหลี่ยมด้านขนาน เรียกว่า ปริซึม การเรียกชื่อปริซึมมีหลายลักษณะขึ้นอยู่กับหน้าตัดของรูปนั้นๆ การเรียกชื่อปริซึม นิยมเรียกชื่อตามลักษณะรูปเหลี่ยมของฐาน
สูตรพื้นที่ผิวและปริมาตรของปริซึม
พื้นที่ผิวข้างของปริซึม พื้นที่ผิวข้างของปริซึม = ความยาวเส้นรอบฐาน × ความสูง
พื้นที่ผิวของปริซึม พื้นที่ผิวทั้งหมดของปริซึม = พื้นที่ผิวข้าง + พื้นที่หน้าตัดหัวท้าย
ปริมาตรของปริซึม ปริมาตรของปริซึม = พื้นที่ฐาน × สูง
ตัวอย่างที่ 4 จงหาพื้นที่ผิวของแท่งปริซึมสามเหลี่ยมนี้
วิธีทำ จากสูตร พื้นที่ผิวทั้งหมดของปริซึม = พื้นที่ผิวข้าง + พื้นที่หน้าตัดหัวท้าย
ขั้นที่ 1 หาพื้นที่ผิวข้าง
จากสูตร พื้นที่ผิวข้างปริซึม = ความยาวรอบฐาน ×ความสูง
จาก ทบ.ปีทาโกรัส เมื่อพิจารณาที่หน้าตัดแล้ว
จะได้ว่า ความยาวของหน้าตัด ด้านที่โจทย์ยังไม่ได้กำหนด ยาว = 10 หน่วย
ดังนั้น พื้นที่ผิวข้างปริซึม = ( 6 + 8 + 10 ) × 12
= 288 ตารางหน่วย
ขั้นที่ 2 หาพื้นที่หน้าตัดหัวท้าย
จากสูตร พื้นที่หน้าตัดหัวท้าย = 2 × พื้นที่ฐานสามเหลี่ยม
= 2 × (½ × ฐาน × สูง)
= 1 × 6 × 8
= 48
ดังนั้น พื้นที่หน้าตัดหัวท้าย = 48 ตารางหน่วย
ขั้นที่ 3 หาพื้นที่ผิวทั้งหมด
จากสูตร พื้นที่ผิวทั้งหมดของปริซึม = พื้นที่ผิวข้าง + พื้นที่หน้าตัดหัวท้าย
= 288 + 48
= 336 ตารางหน่วย
ตอบ 336 ตารางหน่วย
ตัวอย่างที่ 5 จงหาปริมาตรของปริซึมสี่เหลี่ยมคางหมูนี้
วิธีทำ สูตร พื้นที่ฐานปริซึมสี่เหลี่ยมคางหมู = 1/2 × ผลบวกของด้านคู่ขนาน × สูง
= 1/2 × (7 + 13) × 9
= 90 ตารางหน่วย
สูตร ปริมาตรปริซึม = พื้นที่ฐาน × สูง
= 90 × 24
= 2,160 ลูกบาศก์หน่วย
ตอบ 2,160 ลูกบาศก์หน่วย
พื้นที่ผิวและปริมาตรของทรงกลม
ทรงสามมิติที่มีผิวโค้งเรียบและจุดทุกจุดบนผิวโค้ง อยู่ห่างจากจุดคงที่จุดหนึ่งเป็นระย
เท่ากัน เรียกว่า ทรงกลม จุดคงที่นั้นเรียกว่า จุดศูนย์กลางของทรงกลม และระยะทางที่เท่ากันนั้น เรียกว่า รัศมีของทรงกลม
สูตรพื้นที่ผิวและปริมาตรของทรงกลม
พื้นที่ผิวของทรงกลม พื้นที่ผิวของทรงกลม = 4¶r2
ปริมาตรของทรงกลม ปริมาตรของทรงกลม = 4/3¶r3 เมื่อ r แทน รัศมีของวงกลม
ตัวอย่างที่ 6 ขันครึ่งทรงกลม วัดเส้นผ่านศูนย์กลางภายนอกปากขันได้ยาว 14 นิ้ว ขันใบนี้มีพื้นที่ผิวภายนอกเท่าไร
วิธีทำ ขันมีรัศมี 7 นิ้ว
พื้นที่ผิวครึ่งทรงกลม = 2¶r2
= 2 × 22/7 × 7 × 7
= 308 ตารางนิ้ว
ดังนั้น ขันใบนี้มีพื้นที่ผิวภายนอกเท่ากับ 308ตารางนิ้ว
ตอบ 308 ตารางนิ้ว
พื้นที่ผิวและปริมาตรของทรงกระบอก
ทรงสามมิติใดที่มีฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยู่ในระนาบที่ขนานกันเมื่อตัดทรงสามมิตินี้ด้วยระนาบที่ขนานกับฐาน จะได้หน้าตัดเป็นรูปวงกลมที่เท่ากันทุกประการกับฐานเสมอ เรียกทรงสามมิตินี้ว่า ทรงกระบอก
สูตรพื้นที่ผิวและปริมาตรของทรงกระบอก
พื้นที่ฐานหรือพื้นที่หน้าตัด พื้นที่รูปวงกลม = ¶r2
พื้นที่ผิวข้างของทรงกระบอก พื้นที่ผิวข้างของทรงกระบอก = 2¶rh
พื้นที่ผิวของทรงกระบอก พื้นที่ผิวของทรงกระบอก =2¶rh + 2(¶r2)
ปริมาตรของทรงกลม ปริมาตรของทรงกระบอก = ¶r2h
เมื่อ r แทนรัศมีของฐาน และ h แทนความสูงทรงกระบอก
พื้นที่ผิวและปริมาตรของกรวย
ทรงสามมิติใดที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่บนระนาบเดียวกับฐานและเส้นที่เชื่อมต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรง เรียกทรงสามมิตินั้นว่า กรวย
ความสัมพันธ์ของด้านรัศมี (r) ความสูง (h) และ สูงเอียง (l)
ตามทฤษฎีบทปีทาโกรัส จะได้ว่า r2 + h2 = l2
สูตรพื้นที่ผิวและปริมาตรของกรวย
พื้นที่ฐานเป็นรูปวงกลม พื้นที่ฐาน = ¶r2
พื้นที่ผิวข้างของกรวย พื้นที่ผิวข้างของกรวย = ¶rl
พื้นที่ผิวของกรวย พื้นที่ผิวของกรวย = ¶rl + ¶r2
ปริมาตรของปริซึม ปริมาตรกรวย = 1/3¶r2h
เมื่อ r แทนรัศมีกรวย และ h แทนส่วนสูงของกรวย
ตัวอย่างข้อสอบ
1.กรวยใส่ขนมมีเส้นผ่านศูนย์กลางของปากกรวยยาว3 เซนติเมตร สูง 10 เซนติเมตร จงหาความจุของกรวยนี้
วิธีทำ เนื่องจากสูตรปริมาตร (หรือความจุ) ของกรวย =1/3¶r2h
ดังนั้น สิ่งที่เราต้องหาคือ รัศมี (r) และ ความสูง (h)
แต่โจทย์กำหนดความสูงมาให้แล้ว ก็หาแต่รัศมี
ขั้นที่ 1 หารัศมี
โจทย์กำหนดให้ เส้นผ่านศูนย์กลางของปากกรวยยาว 3 ซม.
ดังนั้น รัศมีกรวยยาว = 3 ÷ 2 = 1.5 ซม.
ขั้นที่ 2 หาปริมาตรกรวย
จากสูตร ปริมาตรกรวย = 1/3¶r2h
= 1/3 × 22/7 × (1.5)2 × 10
ดังนั้น ปริมาตรกรวย = 35.57 ลบ.ซม.
ตอบ 357 ลบ.ซม.
2.แท่งไม้รูปร่างเป็นกรวยอันหนึ่งมีเส้นผ่านศูนย์กลางยาว 12 เซนติเมตร สูง 8 เซนติเมตร จงหาพื้นที่ผิวกรวยนี้
วิธีทำ เนื่องจาก พื้นที่ผิวกรวย = ¶rl + ¶r2
ดังนั้น สิ่งที่ต้องหาคือ รัศมีและสูงเอียง (เพื่อจะนำไปแทนค่าลงในสูตรหาพื้นที่ผิวกรวย)
ขั้นที่ 1 หารัศมี
โจทย์กำหนดให้ เส้นผ่านศูนย์กลางยาว 12ซม.
ดังนั้น รัศมีกรวยยาว = 12 ÷ 2 = 6 ซม.
ขั้นที่ 2 หาสูงเอียง
กำหนดให้สูงเอียง = l ซม.
จากทบ.ปีทาโกรัส จะได้ว่า
r2 + h2 = l2
62 + 82 = l2
36 + 64 = l2
l2 = 100
ดังนั้น l = 10 ซม.
ขั้นที่ 3 หาพื้นที่ผิวของกรวย
จากสูตร พื้นที่ผิวของกรวย = ¶r(l + r)
แทนค่าสูตร จะได้ = 22/7 × 6 × (10 + 6)
= 132/7 × 16
ดังนั้น พื้นที่ผิวของกรวย ≈ 301.71 ตร.ซม.
ตอบ 301.71 ตร.ซม.
พีระมิด
ในทางคณิตศาสตร์ ให้ความหมายคำว่า พีระมิด ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยู่บนระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น เรียกว่า พีระมิด
สูตรคำนวณต่างๆที่เกี่ยวกับพีระมิด
พื้นที่ผิวข้างของพีระมิด = 1/2 X ความยาวรอบฐาน X สูงเอียง
= พื้นที่ของหน้าทุกหน้ารวมกัน
พื้นที่ผิวของพีระมิด = พื้นที่ผิวข้างของพีระมิด X พื้นที่ฐานของพีระมิด
ตัวอย่าง จงหาพื้นผิวข้างของพีระมิดห้าเหลี่ยมด้านเท่ามุมเท่าฐานยาวด้านละ 10 เซนติเมตรและส่วนสูงเอียงยาว 6 เซนติเมตร
วิธีคิดคือ พื้นผิวข้างของพีระมิดห้าเหลี่ยมด้านเท่ามุมเท่า = 1/2 x ความยาวของฐาน x สูงเอียง
= 1/2 x (5×10) x 6
= 150 ตารางเซนติเมตร
ลักษณะของพีระมิดตรง
1. หน้าของพีระมิดตรงเป็นรูปสามเหลี่ยมหน้าจั่ว และเท่ากันทุกรูป
2. สันของพีระมิดตรงจะยาวเท่ากันทุกเส้น
3. ความสูงเอียงของพีระมิดตรงด้านเท่า มุมเท่า จะยาวเท่ากันทุกเส้น
4. ปริมาตรของพีระมิด เป็นหนึ่งในสามของปริมาตร ปริซึมที่มีฐานเท่ากันกับพีระมิดและมีส่วนสูงเท่ากับพีระมิด
การหาส่วนต่าง ๆ ของพีระมิด
1. โจทย์ พีระมิดฐานสี่เหลี่ยมผืนผ้า กว้าง 10 เซนติเมตร ยาว 18 เซนติเมตร และความสูงของพีระมิดเป็น 12 เซนติเมตร จงหาความสูงเอียงทั้ง 2 ด้าน พีระมิดเป็น 12 เซนติเมตร จงหาความสูงเอียงทั้ง 2 ด้าน
(1) ความสูงเอียงด้านกว้าง
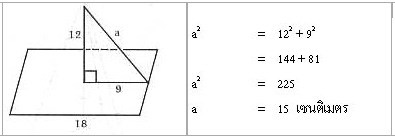
(2) ความสูงเอียงขนานด้านยาว
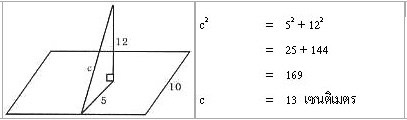
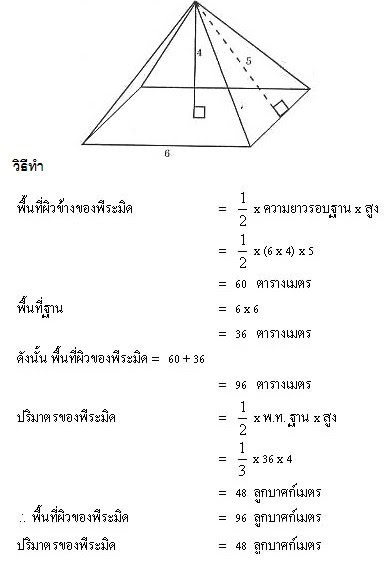
ตัวอย่าง พีระมิดแห่งหนึ่งมีฐานเป็นรูปสี่เหลี่ยมจัตุรัส ยาวด้านละ 6 เมตร สูงเอียง 5 เมตร และสูงตรง 4 เมตร จงหาพื้นที่ผิวและปริมาตรของพีระมิด
กรวย
ในทางคณิตศาสตร์ให้ความหมายคำว่า กรวย ดังนี้
รูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรง เรียกรูปเรขาคณิตสามมิตนั้นว่า กรวย
สูตรคำนวณต่างๆที่เกี่ยวข้องกับกรวย
ปริมาตรของกรวย = 1/3 X (22/7 หรือ 3.14) X รัศมียกกำลังสอง X สูงตรง
พื้นที่ผิวของกรวย = (22/7 หรือ 3.14) X รัศมี X สูงเอียง + (22/7 หรือ 3.14) X รัศมียกกำลังสอง
ตัวอย่าง แท่งไม้รูปร่างเป็นกรวยอันหนึ่งมีเส้นผ่านศูนย์กลางยาว 12 เซนติเมตร สูง 8 เซนติเมตร จงหาพื้นที่ผิวกรวยนี้
วิธีทำ เนื่องจาก พื้นที่ิผิวกรวย = ¶rl + ¶r2
ดังนั้น สิ่งที่เราต้องหา คือ รัศมี และ สูงเอียง (เพื่อจะนำไปแทนค่าลงในสูตรหาพื้นที่ผิวกรวย)
ขั้นที่ 1 หารัศมี
โจทย์กำหนดให้ เส้นผ่านศูนย์กลางยาว 12 ซม.
ดังนั้น รัศมีกรวยยาว = 12 ÷ 2 = 6 ซม.
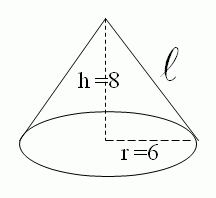
ขั้นที่ 2 หาสูงเอียง
กำหนดให้สูงเอียง = l ซม.
จากทบ.ปีทาโกรัส จะได้ว่า
r2 + h2 = l2
62 + 82 = l2
36 + 64 = l2
l2 = 100
ดังนั้น l = 10 ซม.
ขั้นที่ 3 หาพื้นที่ผิวของกรวย
จากสูตร พื้นที่ผิวของกรวย = ¶r(l + r)
แทนค่าสูตร จะได้ = 22/7 × 6 × (10 + 6)
= 132/7 × 16
ดังนั้น พื้นที่ผิวของกรวย ≈ 301.71 ตร.ซม.
ตอบ 301.71 ตร.ซม.






