พื้นฐานเซต (Set) ม.4

เซต คืออะไร

เซต คือ กลุ่มของสมาชิก (element) ของสิ่งที่สนใจ เช่น เซตของวันในหนึ่งสัปดาห์ หมายถึง กลุ่มของวันจันทร์ อังคาร พุธ พฤหัสบดี ศุกร์ เสาร์ และอาทิตย์ เป็นต้น ซึ่งคำว่าเซตนั้นมีคุณสมบัติที่สำคัญคือ ต้องสามารถระบุได้ว่า อะไรอยู่ในเซต อะไรไม่อยู่ในเซต โดยเราสามารถเขียนเซตได้

แผนภาพของเวนน์–ออยเลอร์ และการดำเนินการของเซต

แผนภาพของเวนน์–ออยเลอร์ (Venn-Euler Diagram)

เป็นแผนภาพที่นิยมใช้เขียนเพื่อแสดงความสัมพันธ์ของเซต เพื่อให้ดูง่ายและชัดเจนมากขึ้น ปกติจะกำหนดเอกภพสัมพัทธ์ด้วยกรอบสี่เหลี่ยมมุมฉาก ภายในนั้นมีเซตซึ่งอาจเขียนเป็นวงกลม วงรี หรือรูปปิดอื่นๆ

สมมติเรามีเซตต่างๆ ดังภาพต่อไปนี้

การพิจารณาเกี่ยวกับเซตจะง่ายขึ้น ถ้าเราใช้แผนภาพของเวนน์-ออยเลอร์ เข้ามาช่วย หลักการเขียนแผนภาพมีดังนี้

1. ใช้รูปสี่เหลี่ยมผืนผ้าหรือสี่เหลี่ยมมุมฉากแทนเอกภพสัมพัทธ์

2. ใช้วงกลมหรือวงรีหรือรูปปิดใด ๆ แทนเซตต่าง ๆ ที่เป็นสมาชิกของ และเขียนภายในสี่เหลี่ยมผืนผ้า

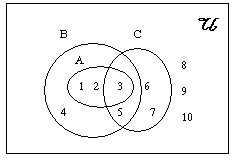
ถ้ากำหนดให้ U = {1,2,3,4,5,6,7,8,9,10} A = {1,2,3} , B = {1,2,3,4,5} , C = {3,5,6,7}

เราจะเขียนแผนภาพเวนน์–ออยเลอร์ แสดงเอกภพสัมพัทธ์ U และเซตย่อยต่าง ๆ ดังแผนภาพต่อไปนี้

การใช้แผนภาพเวนน์–ออยเลอร์ ในการตรวจสอบความสมเหตุสมผล

เราจะวาดแผนภาพตามสมมติฐานที่เป็นไปได้ แล้วพิจารณาว่าแผนภาพแต่ละกรณีแสดงผลสรุปตามที่สรุปไว้หรือไม่ ถ้าทุกกรณีแสดงผลตามที่กหนด แสดงว่าสมเหตุสมผล ถ้ามีแผนภาพที่ไม่แสดงผลตามที่สรุปไว้ การสรุปนั้นไม่สมเหตุสมผล โดยจะใช้การอ้างเหตุผลโดยตรรกบทของตรรกศาสตร์เข้ามาตรวจสอบ

ในการใช้แผนภาพเพื่อตรวจสอบความสมเหตุสมผล จะต้องวาดแผนภาพตามเหตุผลหรือสมมติฐานทุกกรณีที่เป็นไปได้ ถ้าทุกกรณีแสดงผลตามที่กำหนด จะได้ว่าข้อสรุปนั้น สมเหตุสมผล แต่ถ้ามีบางกรณีที่ไม่สอดคล้องกับผลสรุปแล้ว ผลสรุปนั้นจะไม่สมเหตุผมผล …

ภาพจาก Mayitutoryou

มาดูแผนภาพของเวนน์-ออยเลอร์ เป็นแผนภาพที่ใช้แสดงความเกี่ยวข้องของเซต เพื่อช่วยในการคิดคำนวณหรือแก้ปัญหา ซึ่งตัวชื่อแผนภาพตามชื่อของนักคณิตศาสตร์คือ เวนน์และออยเลอร์ การเขียนแผนภาพเวนน์-ออยเลอร์ มีวิธีการเขียนดังนี้

ให้ เอกภพสัมพทธ์ U แทนด้วยรูปสี่เหลี่ยมผืนผ้าหรือรูปปิดใด ๆ

เซต A, B, C, . . . ซึ่งเป็นสับเซตของ U แทนด้วยวงกลม วงรี หรือรูปปิดอื่น ๆ โดยให้เซต A, B, C, . . . อยู่ใน U ดังตัวอย่าง

ตัวอย่างที่ 1 กำหนด U = {1, 2, 3, . . .} , A = {1, 2, 3, 4, 5} และ B = {2, 4, 6, 8}

จงเขียนแผนภาพของเวนน์-ออยเลอร์แทนเซต

วิธีทำ เซต A และเซต B มีสมาชิกร่วมกันคือ 2 และ 4 ซึ่งสามารถเขียนแผนภาพ

แทนเซต A และ B ได้ดังนี้

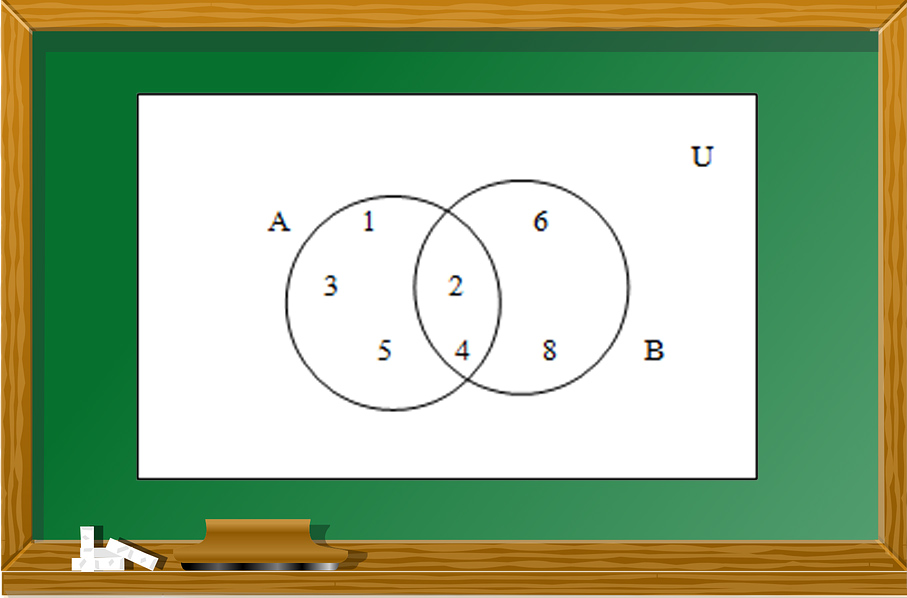
ตัวอย่างที่ 2 กำหนด U = {a, b, c, . . . , z} , A = {a, b, c, d} , B = {e, f, g}

และ C = {h, i, j, k} จงเขียนแผนภาพเวนน์-ออยเลอร์

วิธีทำ เขียนแผนภาพเวนน์-ออยเลอร์ แทน A, B และ C ได้ดังนี้

ตัวอย่างที่ 3 กำหนด U = {x | x เป็นจำนวนนับที่น้อยกว่า 20}

A = {x | x เป็นจำนวนนับที่น้อยกว่า 10}

B = {x | x เป็นจำนวนคี่บวกที่น้อยกว่า 7}

จงเขียนแผนภาพเวนน์-ออยเลอร์

วิธีทำ U = {x | x เป็นจำนวนนับที่น้อยกว่า 20}

\ U = {1, 2, 3, . . . , 19}

A = {x | x เป็นจำนวนนับที่น้อยกว่า 10}

\ A = {1, 2, 3, . . . , 9}

B = {x | x เป็นจำนวนคี่บวกที่น้อยกว่า 7}

\ B = {1, 3, 5}

เขียนแผนภาพแทน A และ B ได้ดังนี้

ชนิดของเซท

เซตว่าง (Empty Set หรือ Null Set) หมายถึง เซทที่ไม่มีสมาชิกหรืออาจะกล่าวได้ว่าเซตว่างมีสมาชิก 0 สมาชิก โยสัญลักษณ์ที่ใช้ คือ { }
เซตจำกัด (Finite Set) หมายถึง เซตที่สามารถนับจำนวนสมาชิกได้ครบถ้วน สามารถบอกได้ว่ามีจำนวนสมาชิกเท่าใด เป็นจำนวนเต็มบวกหรือศูนย์
เซตอนันต์ (Infinite Set) หมายถึง เซตที่มีจำนวนสมาชิกมากมายนับไม่ถ้วน ไม่สามารถบอกได้ว่ามีจำนวนเท่าใด
เซตเท่ากัน (Equal Set) หมายถึง เมื่อ A และ B เป็นเซตใดๆ A จะเรียกว่าเท่ากับ B ก็ต่อเมื่อเซตทั้งสองมีจำนวนสมาชิกเท่ากันและเหมือนกันทุกสมาชิก ซึ่งจะเขียนแทนด้วยสัญลักษณ์ A – B หรืออาจกล่าวได้ว่าเซตสองเซตใดๆ จะเท่ากันก็ต่อเมื่อสมาชิกของ A ทุกสมาชิกเป็นสมาชิกของ B และสมาชิกทุกสมาชิกของ B เป็นสมาชิกของ A นั่นคือ A = B ก็ต่อเมื่อ ถ้า x ϵ A แล้ว X ϵ B และ ถ้า X ϵ B แล้ว X ϵ A
เซตเสมอเหมือนกัน (Equivalent Set) คือ เซต 2 เซตใดๆ ที่มีจำนวนสมาชิกเท่ากันแต่ไม่เหมือนกันทุกตัว เรียกว่า เซตเสมอ ฃเหมือน A เสมอเหมือน B จะเขียนแทนด้วย A ≡ B นั่นคือเซต 2 เซตที่เท่ากันเสมอเหมือนกัน แต่เซต 2 เซตที่เสมอเหมือนกันอาจจะเท่ากัน หรือไม่เท่ากันก็ได้
สับเซต (Sub Set) กำหนด A และ B เป็นเซตใดๆ A จะเรียกเป็นสับเซตของ B ซึ่งเขียนแทนด้วยสัญลักษณ์ A C Bก็ต่อเมื่อ X ϵ A แล้ว X ϵ B
พาวเวอร์เซท (Power Set) คือ เซตของสับเซตทั้งหมดของเซต A เมื่อ A เป็นเซตจำกัด เพาเวอร์เซตของเซต A เขียนแทนด้วย P(A)

การนับจำนวนสมาชิกในเซต

จำนวนสมาชิกของเซต A เขียนแทนด้วย n(A)
ถ้าสมาชิกในเซตซ้ำกันให้เขียนเพียงครั้งเดียว

ชนิดของเซต

เซตจำกัด คือ เซตที่สามารถบอกได้ว่ามีสมาชิกทั้งหมดกี่ตัว
เซตอนันต์ คือ เซตที่ไม่สามารถบอกได้ว่ามีสมาชิกทั้งหมดกี่ตัว
เซตว่าง คือ เซตที่ไม่มีสมาชิกในเซตเลย หรือเขียนแทนด้วย ∅

เอกภพสัมพัทธ์ (U) คือ เซตที่กำหนดขอบเขตสิ่งที่เรากำลังพิจารณา

ความสัมพันธ์ระหว่างเซต

เซตที่เท่ากัน คือ เซตที่สมาชิกทุกตัวเหมือนกัน ถ้าเซต A เท่ากับเซต B จะเขียนแทนด้วยสัญลักษณ์ A = B
เซตที่เทียบเท่ากัน คือ เซตที่จำนวนสมาชิกเท่ากัน

สมบัติของสับเซต

ถ้า A⊂B และ A ≠ B จะเรียก A ว่าเป็นสับเซตแท้ของ B
ถ้า A เป็นเซตจำกัด จะมีสมาชิก n ตัว แล้ว A มีสับเซตทั้งหมด 2ⁿสับเซต
ถ้า A เป็นเซตจำกัด จะมีสมาชิก n ตัว แล้ว A มีสับเซตแท้ทั้งหมด 2ⁿ-1 สับเซต
Φ ⊂ A (เซตว่างเป็นสับเซตทุกเซต)
A ⊂ A (ตัวเองก็เป็นสับเซตของตัวเอง)
ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C
A ⊂ B และ B ⊂ A ก็ต่อเมื่อ A = B

หมายเหตุ : Φ ( เซตว่าง ) ไม่มีสับเซต

ซับเซตและเพาเวอร์เซต ( subset & power set)

สับเซต (Subset)

ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B

ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ B เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B

ตัวอย่าง การเป็นสับเซตและไม่เป็นสับเซตกัน

กำหนดให้ A={1,2,3,4,5},B={2,3,5} และ C={2,4}

จะเห็นว่าสมาชิกทุกตัวของ B คือ 2,3 และ 5 เป็นสมาชิกของ A ด้วย ดังนั้น B ⊂ A และสมาชิกของ C คือ 2 และ 4 ก็เป็นสมาชิกของ A ด้วยเช่นกัน ดังนั้น C ⊂ A แต่ในขณะที่สมาชิกของ C ตัวหนึ่ง คือ 4 ไม่เป็นสมาชิกของ B ดังนั้น C ⊄ B

สมบัติของสับเซต

1) A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)

2) A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)

3) ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)

4) ถ้า A ⊂ ø แล้ว A = ø

5) ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)

6) A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A

7) ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต

เพาว์เวอร์เซต ( power set )

ถ้า A เป็นเพาว์เวอร์เซต (Power Set) ของเซต A คือ เซตที่มีสมาชิกประกอบไปด้วยสับเซตของ A ทั้งหมด

เพาเวอร์เซตของ A เขียนแทนด้วย P(A) = {สับเซตทั้งหมดของA}

เช่น ถ้า A={1,2} สับเซตของ A คือ ∅,{1},{2},{1,2}หรือ A

ดังนั้น P(A)={∅,{1},{2},A}

คุณสมบัติของเพาว์เวอร์เซต

กำหนดให้ A และ B เป็นเซตใดๆ

1. ∅∈P(A) เพราะ ∅⊂A เสมอ

2. ∅⊂P(A) เพราะเซตว่างเป็นสับเซตของทุกเซต แล้ว P(A) ก็เป็นเซตเช่นกัน

3. A∈P(A) เพราะ A⊂Aเสมอ

4. ถ้า A เป็นเซตจำกัด และ n(A) คือจำนวนสมาชิกของ A แล้วP(A)จะมีสมาชิก2n(A) ตัว (เท่ากับจำนวนสับเซตของ A)

5. A⊂B ก็ต่อเมื่อ P(A)⊂P(B)

6. P(A)∩P(B)=P(A∩B)

การหาสับเซตทั้งหมดของA

จำนวนสับเซตทั้งหมดหาได้จาก 2ⁿ เมื่อ n = จำนวนสมาชิกในเซต

ตัวอย่าง จงหาสับเซตทั้งหมดของ A เมื่อ A = {2, 4, 6, 8}

A จะมีสับเซตทั้งหมด 2⁴ =16 สับเซต เมื่อแจกแจงสับเซตทั้งหมดจะได้ดังนี้

{2} {4} {6} {8}

{2, 4} {2, 6} {2, 8} {4, 6} {4, 8} {6, 8}

{2, 4, 6} {2, 6, 8} {2, 4, 8} {4, 6, 8}

{2, 4, 6, 8}

ความหมายของสับเซตแท้

สับเซตแท้ คือ สับเซตทั้งหมดที่ไม่ใช่ตัวมันเอง มี 2ⁿ– 1 สับเซต (เซตว่างไม่มีสับเซตแท้)

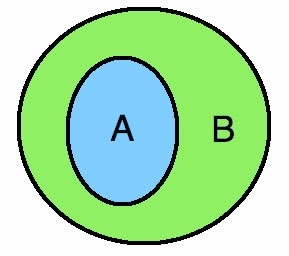
นิยาม A เป็นสับเซตแท้ของ B ก็ต่อเมื่อ A⊂B และ A ≠ B

ซึ่งจะได้รูปดังภาพ

โจทย์ประยุกต์ เรื่อง สับเซต

การหาจำนวนสับเซตทั้งหมดของ A

หลักในการเขียนสับเซตทั้งหมดของเซตๆหนึ่งที่โจทย์กำหนดมาทำโดย เริ่มเขียนตั้งแต่เซตว่าง แล้วตามด้วยเซตที่มีสมาชิก 1 ตัว, 2 ตัว ไปเรื่อยๆ จนมีสมาชิกเท่ากับเซตที่โจทย์กำหนดมา (ตัวมันเอง) โดยสมาชิกที่นำมาใช้เขียนต้องเป็นสมาชิกของเซตที่โจทย์กำหนดมาด้วย

ตัวอย่าง จงเขียนสับเซตทั้งหมดของเซตต่อไปนี้

1. A = Ø สับเซตทั้งหมดของ A มี 1 สับเซต คือ Ø

2. B = {1} สับเซตทั้งหมดของ B มี 2 สับเซต คือ 1) Ø 2) {1}

3. C = {1,3} สับเซตทั้งหมดของ C มี 4สับเซต คือ 1) Ø 2) {1} 3) {3} 4) {1,3}

4. D = {1,3,5} สับเซตทั้งหมดของ D มี 4 สับเซต คือ1) Ø 2) {1} 3) {3} 4) {5} 5) {1,3} 6)

{1,5} 7) {3,5} 8) { 1,3,5}

เซต

จำนวนสมาชิกของเซต

จำนวนสับเซตทั้งหมด

1. A = Ø

2. B = { 1 }

3. C = { 1 , 3 }

4. D = { 1 , 3 , 5 }

2⁰ = 1

2¹ = 2

2² = 4

2³ = 8

จากตาราง พิจารณาความสัมพันธ์ของสมาชิกของเซตกับจำนวนสับเซตทั้งหมดจะได้ว่า

จำนวนสับเซตทั้งหมดของเซต A = 2ⁿ⁽^A⁾

จำนวนสับเซตแท้ทั้งหมดของ A และตัวอย่าง

นิยาม : สับเซตแท้ (proper set) ของ A คือ สับเซตทั้งหมดของเซต A ยกเว้น ตัวมันเอง (ยกเว้น A)

1.มีเซตอะไรไหมที่ไม่มีสับเซตแท้
ตอบ มี เซตดังกล่าวคือเซตว่าง เพราะว่าสับเซตของ Ø ก็คือ Ø เพียงตัวเดียว ดังนั้น เซตว่างจึงไม่มีสับเซต

แท้

2. จำนวนสับเซตแท้ของเซต A = 2^n(A) -1 สับเซต

โจทย์ประยุกต์ เรื่อง สับเซต

ข้อ1. ถ้า A={a, b,c,d,e,f} และ B={a,b} แล้วจำนวนเซต X ซึ่ง B⊂X⊂A เท่ากับข้อใดต่อไปนี้

1.4 2.15 3.16 4.32

เฉลย.

B⊂Xแปลว่า a, b ต้องอยู่ใน X ซึ่ง X⊂Aแปลว่า c, d, e, f อยู่ใน X กี่ตัวก็ได้

∴จำนวนแบบที่เป็นไปได้ของ X ก็คือจำนวนสับเซตทุกแบบของ {c, d, e, f}

นั่นคือ 2^4=16 แบบ

ข้อ2. ถ้า A={5, 6, 7, …,20} และ B={1, 2, 3,…,15} แล้ว จำนวนสมาชิกในเซต {X | X เป็นสับเซตของ A และ X ไม่เป็นสับเซตของ B}

1. (7×2)^10 2. (31×2)^11

3. (31×2)^10 4. (63×2)^11

เฉลย.

คิดโดยวิธีลบออก คือ จำนวนสับเซตของ A ทุกแบบ ลบออกด้วยแบบที่เป็นสับเซตของ B ด้วย

จะได้เท่ากับ 2^16-2^11=31×2^11

ข้อ3. กำหนดให้ S={1, 2, 3, 4, 5} , A={1} , B={5} และ A⊂X⊂S , B⊂Y⊂S จงหาว่า X∪Y มีทั้งหมดกี่เซตที่แตกต่างกัน

1.8 2.16 3.32 4.64

เฉลย.

แบบต่างๆของ X คือ

{1, สับเซตทุกแบบของ 2,3, 4,5}

มีอยู่ 2^4=16 แบบ

แบบต่างๆของ Y คือ

{5, สับเซตทุกแบบของ 1, 2, 3, 4}

มีอยู่ 2^4=16 แบบ

แต่แบบต่างๆของ X∪Y จะต้องมีทั้ง 1 และ 5 อยู่ในนั้น คือ {1, 5, สับเซตทุกเเบบของ 2, 3, 4}

ดังนั้นจึงมีอยู่ 2^13= 8 แบบ

เรื่องพาวเวอร์เซต และตัวอย่าง

หมายถึง เซตของสับเซต จะเขียนแทนเพาเวอร์เซตของเซต A ด้วย P(A)

วิธีหาเพาเวอร์เซต จะต้องหาสับเซตทั้งหมดให้ได้ก่อน จากนั้นจึงใส่เซตครอบลงไป

ตัวอย่าง จงหาสับเซตทั้งหมดของ A = {2, 4, 6, 8}

ขั้นแรก : หาสับเซตก่อน ได้แก่

Ø , {2} , {4} , {6} , {8} , {2, 4} , {2, 6} , {2, 8} , {4, 6} , {4, 8} , {6, 8} , {2, 4, 6} , {2, 6, 8} , {2, 4, 8} , {4, 6, 8} , {2, 4, 6, 8}

ดังนั้น P(A) = {Ø, {2},{4},{6},{8},{2, 4},{2, 6},{2, 8},{4, 6},{4, 8},{6, 8}, {2, 4, 6}, {2, 6, 8},{2, 4, 8},{4, 6, 8},{2, 4, 6, 8}

กำหนดให้ A เป็นเซตจำกัด ถ้าเซต A มีจำนวนสมาชิก ตัวแล้วจำนวนสมาชิกของเพาเวอร์เซต A จะเท่ากับ 2ⁿตัว

ตัวอย่าง

1. ถ้า P(P(A)) มีสมาชิก 256 ตัว แล้วเซต A จะมีสมาชิกกี่ตัว

วิธีทำ

P(P(A)) = 256 = 2^8

P(A) = 8= 2^3

n(A) = 3

2. ถ้า n(P(A)) – n(P(B)) = 63 และn(P(A∩B)) + n(P(A∪B)) = n(P(C∩B)) + n(P(C∪B)) แล้ว จงหาค่าของ n(A) + n(B) + n(C)

วิธีทำ

2^(n(A)) – 2^(n(B)) = 2^6 – 2^0

∴n(A) = 6 , n(B) = 0จะได้ว่า B =∅

แทนค่าได้

n(P(A∩∅)) + n(P(A∪∅)) = n(P(C∩∅)) + n(P(C∪∅))

n(P(∅)) + n(P(A)) = n(P(∅)) + n(P(C))

2^n(A) = 2^n(C)

∴n(A) = n(C) = 6

∴n(A) + n(B) + n(C) = 6+0+6 = 12

พื้นฐานเซต (Set) ม.4

เซต คืออะไร

ชนิดของเซท

การนับจำนวนสมาชิกในเซต

ชนิดของเซต

ความสัมพันธ์ระหว่างเซต

สมบัติของสับเซต

ซับเซตและเพาเวอร์เซต ( subset & power set)

Author: tmtyai

Related Posts