เมทริกซ์ (Matrix) คณิตศาสตร์ ม.6

นิยามเรื่องเมทริกซ์ (Matrix ) คือ การนำเลขจำนวนจริง หรือจำนวนเชิงซ้อนมาเขียนเรียงกันเป็นแถวๆ ภายในวงเล็บเล็ก หรือวงเล็บใหญ

การบอกตำแหน่งของสมาชิก

มิติและสัญลักษณ์ของเมทริกซ์
เมทริกซ์ที่มี m แถว n หลัก เรียกว่า m n เมทริกซ์ และเรียน m x n ว่า มิติ
ของเมทริกซ์ และมีสมาชิก mn จ านวน
โดยทั่วไปเราสามารถเขียน a ij แทนสมาชิกของเมทริกซ์ในแถวที่ i หลักที่ j

ทรานสโพสเมทริกซ์และการเท่ากันของเมทริกซ์

ทรานสโพสของเมตริกซ์หรือก็คือเมทริกซ์สลับเปลี่ยนนั่นเองครับอันเดียวกันครับบางคนเรียกทับศัพท์ภาษาอังกฤษเลยว่าทรานสโพสของเมทริกซ์(Transpose of matrix) เรื่องนี้ถ้าไปอ่านในบทนิยามตามหนังสือต่างๆอาจจะงงครับเพราะภาษาคณิตศาสตร์เป็นภาษาเชิงสัญลักษณ์และต้องเขียนให้รัดกุมเพื่อไม่ให้เกิดข้อโต้แย้งหรือเกิดความผิดพลาดเข้าใจผิดแตกต่างกันออกไปครับ ดังนั้นเรามาดูความหมายของทรานสโพสเมทริกซ์ในแบบบ้านๆกันครับ

เจ้าทรานสโพสเมทริกซ์ก็คือการนำเมทริกซ์มาสลับ ก็คือ เอาแถวมาสลับเป็นหลักครับ ดังนั้นเขาจึงเรียงเป็นภาษาไทยเมทริกซ์สลับเปลี่ยนครับ….มาดูตัวอย่างกันเลยครับ  สัญลักษณ์ที่ใช้แทนทรานสโพสของเมทริกซ์ก็คือ

มารู้จักกับเมทริกซ์ศูนย์ การบวกลบและการคูณเมทริกซ์ 

สมบัติเกี่ยวกับการบวกของเมทริกซ์

1. สมบัติปิดของการบวก
ถ้า A และ B เป็น m n เมทริกซ์ แล้ว A+B เป็น m n เมทริกซ์’ ดังนั้น การ
บวกเมทริกซ์มีสมบัติการปิด
2. สมบติการสลับที่ของการบวก
ถ้า A และ B เป็น m n เมทริกซ์ แล้ว A+B = B+A ดังนั้น การบวกเมทริกซ์
มีสมบัติกาสลับที่ของการบวก
3. สมบัติการเปลี่ยนกลุ่มได้ของการบวก
ถ้า A, B และ C เป็น m n เมทริกซ์ แล้ว (A+B)+C = A+(B+C) ดังนั้น
การบวกเมทริกซ์มีวมบัติการเปลี่ยนกลุ่มของการบวก
4. เอกลักษณ์การบวก
การบวกเมทริกซ์มี 0 เป็นเอกลักษณ์ สมบัติการมีเอกลักษณ์การบวก ซึ่งเอกลักษณ์การบวกของเมทริกซ์ คือ เมทริกซ์ศูนย์ (สมาชิกทุกตำแหน่งเป็น 0) เขียนแทนด้วย 

5.สมบัติการมีตัวผกผัน คือ ถ้า A เป็นเมทริกซ์ใดๆแล้วจะได้ว่า (-A) เป็นเมทริกซ์ผกผันของ A ซึ่งเมื่อนำ A มาบวกกับ -A แล้วจะได้เมทริกซ์ศูนย์

สมบัติการคูณเมทริกซ์ด้วยจำนวนจริง

ให้ A, B เป็นเมทริกซ์ที่มีมิติ  และ c, d เป็นจำนวนจริง

1. (cd)A = c(dA) = d(cA)  เช่น   
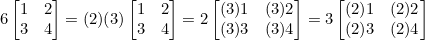
2. c(A + B) = cA + cB
3. (c + d)A = cA + dA
4. 1(A) = A และ -1(A) = -A

สมบัติเกี่ยวกับการคูณเมทริกซ์ด้วยเมทริกซ์

1. สมบัติปิดสำหรับการคูณ
ถ้า A และ B เป็น n n เมทริกซ์’ หรือ เมทริกซ์จัตุรัส จะได้ AB และ BA
เป็น nXn เมทริกซ์ นั่นคือ การคูณเมทริกซ์มีสมบัติปิด

2. สมบัติการสลับที่ของการคูณ
ถ้า A และ B เป็น nΧn เมทริกซ์ จากตัวอย่างข้างต้นจะพบว่า AB ≠ BA ดังนั้น
การคูณเมทริกซ์ไม่มีสมบัติการสลับที่การคูณ
3. สมบัติการเปลี่ยนกลุ่มได้ของการคูณ
4. เอกลักษณ์สำหรับการคูณ
5. อินเวอร์สการคูณ