พื้นที่ พื้นที่ผิว และปริมาตร

พีระมิด

รูปเรขาคณิตสามมิติ มีฐานเป็นรูปหลายเหลี่ยม ผิวด้านข้างเป็นรูปสามเหลี่ยมที่มีจำนวนเท่ากับจำนวนด้านของฐาน มีจุดยอดร่วมกันเพียงจุดเดียว.

1. การเรียกชื่อพีระมิด

การเรียกชื่อพีระมิด นิยมเรียกชื่อตามลักษณะรูปเหลี่ยมของฐาน ตัวอย่างเช่น พีระมิดฐานสี่เหลี่ยมผืนผ้า พีระมิดฐานหกเหลี่ยม เป็นต้น

2. ส่วนประกอบของพีระมิด

พีระมิดแบ่งออกเป็น 2 ลักษณะ คือ พีระมิดตรงและพีระมิดเอียง

พีระมิดตรง หมายถึง พีระมิดที่มีฐานเป็นรูปเหลี่ยมด้านเท่ามุมเท่า มีสันยาวเท่ากันทุกเส้น จะมีสูงเอียงทุกเส้นยาวเท่ากัน และส่วนสูงตั้งฉากกับฐานที่จุดซึ่งอยู่ห่างจากจุดยอดมุมของรูปเหลี่ยมที่เป็นฐานเป็นระยะเท่ากัน มีหน้าทุกหน้าเป็นรูปสามเหลี่ยมหน้าจั่ว ส่วนกรณีที่สันทุกสันยาวไม่เท่ากัน สูงเอียงทุกเส้นยาวไม่เท่ากัน เรียกว่า พีระมิดเอียง

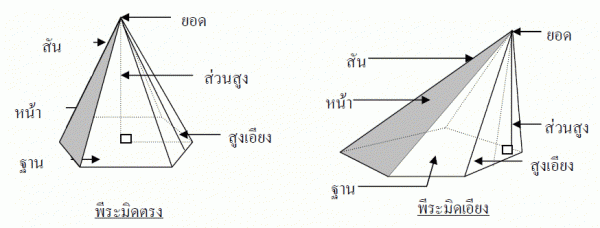
*ข้อสังเกต

1) พีระมิดตรงจะมีฐานเป็นรูปเหลี่ยมด้านเท่า และมีสันทุกเส้นยาวเท่ากัน
2) พีระมิดตรงที่มีฐานเป็นรูปเหลี่ยมด้านเท่ามุมเท่า จะมีสูงเอียงทุกเส้นยาวเท่ากัน
3) ส่วนสูงของพีระมิดตรงใดๆ จะตั้งฉากกัับฐาน ที่จุดซึ่งอยู่่ห่างจากมุมของรูปเหลี่ยมที่เป็นฐาน เป็นระยะเท่ากัน
4) พีระมิดที่มีหน้าทุกหน้าเป็นรูปสามเหลี่ยมหน้าจั่ว จะมีสันทุกเส้นยาวเท่ากัน

3. การหาความยาวด้านต่างๆ ของพีระมิด

การจะหาพื้นที่ผิวและปริมาตรของพีระมิดได้นั้น ควรจะหาความยาวด้านต่างๆ ของพีระมิดให้ได้เสียก่อน

** การหาความยาวด้านต่างๆ มักใช้ทฤษฎีบทปีทาโกรัส

3.1) การหาความสูงเอียง กรณีที่โจทย์กำหนดความยาวสัน

Ex.1 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 6 นี้ว สันยาว 5 นิ้ว จงหาความสูงเอียง

วิธีทำ วาดรูปพีระมิดฐานสี่เหลี่ยมจัตุรัสขึ้นมาก่อน

กำหนดให้ AC เป็นสันยาว 5 นิ้ว และ AB เป็นความสูงเอียง
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 6 ÷ 2 = 3 นิ้ว ตามทฤษฎีปีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AB² + 3² = 5²
AB² = 5² – 3²
AB² = 16
AB = 4
ตอบ สูงเอียงยาว 4 นิ้ว

3.2) การหาความสูงเอียง กรณีที่โจทย์กำหนดส่วนสูง

Ex.2 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 10 นี้ว ส่วนสูงยาว 12 นิ้ว จงหาความสูงเอียง

วิธีทำ วาดรูปพีระมิดฐานสี่เหลี่ยมจัตุรัสขึ้นมาก่อน

กำหนดให้ AC เป็นส่วนสูง ยาว 12 นิ้ว และ AB เป็นความสูงเอียง
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 10 ÷ 2 = 5 นิ้ว ตามทฤษฎีปีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AB² = 12² + 5²
AB² = 144 + 25
AB² = 169
AB = 13
ตอบ สูงเอียงยาว 13 นิ้ว

  3.3) การหาความสูง กรณีโจทย์กำหนดสูงเอียง

Ex.3 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 10 นิ้ว สูงเอียงยาว 13 นิ้ว จงหาความสูง

วิธีทำ วาดรูปพีระมิดฐานสี่เหลี่ยมจัตุรัสขึ้นมาก่อน

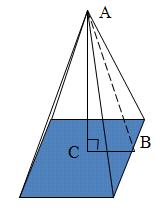ให้ AB เป็นความสูงเอียง, AC เป็นส่วนสูง
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 10 ÷ 2 = 5 นิ้ว ตามทฤษฎีปีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AC² + 5² = 13²
AC² = 169 – 25
AC² = 144
AC = 12
ตอบ ส่วนสูงยาว 12 นิ้ว

4. พื้นที่ผิวของพีระมิด

4.1) พื้นที่ผิวข้าง

เมื่อคลี่พีระมิดออกมา จะได้เป็นรูป

พื้นที่ผิวข้างของพีระมิด ได้แก่พื้นที่ของหน้าทุกหน้าของพีระมิด (ไม่รวมฐาน)
หรือก็คือ พื้นที่ของรูปสามเหลี่ยมทุกรูปรวมกัน นั่นเอง
จาก สูตรพื้นที่ของรูปสามเหลี่ยม = ½ × ฐาน × ความสูง

ดังนั้น

สูตรการหาพื้นที่ผิวข้างของพีระมิด 1 ด้าน = ½ × ฐาน × สูงเอียง
* ในกรณีที่เป็นพีระมิดตรง (ฐานเป็นรูปเหลี่ยมด้านเท่ามุมเท่า)
จะได้ว่า

พื้นที่ผิวข้างของพีระมิด = ½ × ความยาวรอบฐาน × สูงเอียง

พิสูจน์

พื้นที่ผิวข้างของพีระมิด
= พื้นที่สามเหลี่ยมทุกรูปรวมกัน
= (พื้นที่สามเหลี่ยม 1 ด้าน) × จำนวนด้านของฐาน —- จำนวนรูปสามเหลี่ยม จะเท่ากับจำนวนเหลี่ยมหรือด้านของฐาน
= (½ × ฐาน × สูงเอียง) × จำนวนด้านของฐาน
= ½ × [จำนวนด้านของฐาน x ฐาน] x สูงเอียง
↓
= ½ × [ความยาวรอบฐาน] x สูงเอียง
ซตพ.

4.2) พื้นที่ผิว

พื้นที่ผิวของพีระมิด คือ ผลรวมของพื้นที่ผิวข้างทุกด้านของพีระมิด

ดังนั้น

พื้นที่ผิวทั้งหมด = พื้นที่ฐาน + พื้นที่ผิวข้างทุกด้าน

สรุป

1) พื้นที่ของหน้าทุกหน้าของพีระมิดรวมกันเรียกว่า พื้นที่ผิวข้างของพีระมิด
และพื้นที่ผิวข้างของพีระมิดรวมกับพื้นที่ฐานของพีระมิดเรียกว่า พื้นที่ผิวของพีระมิด
2) สูตรการหาพื้นที่ผิวข้างของพีระมิด 1 ด้าน = ½ × ฐาน × สูงเอียง
3) ในกรณีที่เป็นพีระมิดตรง (ฐานเป็นรูปเหลี่ยมด้านเท่ามุมเท่า)
พื้นที่ผิวข้างของพีระมิด = ½ × ความยาวรอบฐาน × สูงเอียง
4) สูตรการหาพื้นที่ผิวทั้งหมด = พื้นที่ฐาน + พื้นที่ผิวข้างทุกด้าน

ตัวอย่างโจทย์

Ex.4 พีระมิดฐานสี่เหลี่ยมจัตุรัสมีด้านฐานยาวด้านละ 10 นิ้ว ส่วนสูงยาว 12 นิ้ว จงหาพื้นที่ผิวข้างพีระมิด

วิธีทำ เนื่องจาก สูตรพื้นที่ผิวข้างของพีระมิด = ½ × ความยาวรอบฐาน × สูงเอียง

แต่โจทย์ไม่กำหนดความยาวสูงเอียง
ดังนั้น ต้องหาความยาวสูงเอียงก่อน

ขั้นที่ 1 หาสูงเอียง

ให้ AC เป็นส่วนสูง ยาว 12 นิ้ว, และ AB เป็นความสูงเอียง
BC เป็นความยาวครึ่งหนึ่งของด้านฐาน ยาว 10 ÷ 2 = 5 นิ้ว ตามทฤษฎีปีทาโกรัส ใน รูปสามเหลี่ยมมุมฉาก ABC
พิจารณาสามเหลี่ยม ABC
AB² = 12² + 5² = 144 + 25 = 169
จะได้่ AB = 13
้ ดังนั้นสูงเอียงยาว 13 นิ้ว

ขั้นที่ 2 หาพื้นที่ผิวข้าง

พื้นที่ผิวข้างของพีระมิด = ½ × ความยาวรอบฐาน × สูงเอียง

ได้พื้นที่ผิวข้างพีระมิด = ½ × ( 10 + 10 + 10 + 10 ) × 13
= ½ × 40 × 13
= 260 ตารางนิ้ว
ตอบ 260 ตารางนิ้ว

5. ปริมาตรของพีระมิด

ปริมาตร คือ ปริมาณที่วัด เพื่อวัดบริเวณที่ว่าง (ความจุ) ภายในรูปทรงสามมิติ
การวัดปริมาตรของรูปทรงสามมิติใช้หน่วยวัดเป็นลูกบาศก์หน่วย

การหาปริมาตรของพีระมิด ให้ทดลองจากกล่องทรงปริซึม

จากสูตร ปริมาตรปริซึม = พื้นที่ฐาน × สูง (จะได้เรียนในบทต่อไป)
เมื่อพีระมิดที่มีส่วนสูงและฐานเท่ากับปริซึม

เมื่อทำการตวง จะได้ 3 ปริมาตรพีระมิด เท่ากับ 1 ปริมาตรปริซึม
ดังนั้น

สูตร ปริมาตรของพีระมิด = ¹/₃ × พื้นที่ฐาน × สูง

Ex.5 จงหาปริมาตรของพีระมิดตรงฐานสี่เหลี่ยมจัตุรัส ที่มีด้านฐานยาวด้านละ 22 เซนติเมตร ส่วนสูง 15 เซนติเมตร

วิธีทำ

สูตร ปริมาตรของพีระมิด = ¹/₃ × พื้นที่ฐาน × สูง
ได้ปริมาตรของพีระมิดนี้ = ¹/₃ × ( ด้าน × ด้าน ) × สูง
= ¹/₃ × ( 22 × 22 ) × 15
= 22 × 22 × 5
= 2,420 ลูกบาศก์เซนติเมตร

ตอบ 2,420 ลบ.ซม.

Ex.6 จงหาปริมาตรของพีระมิดตรงฐานสี่เหลี่ยมจัตุรัส ที่มีด้านฐานยาวด้านละ 14 เซนติเมตร สูงเอียงยาว 25 เซนติเมตร

วิธีทำ เนื่องจาก สูตรของปริมาตรพีระมิด = ¹/₃ × พื้นที่ฐาน × สูง

แต่โจทย์ไม่ได้กำหนดส่วนสูงมากให้
ดังนั้น ต้องหาส่วนสูงก่อน

ขั้นที่ 1 หาส่วนสูง
ให้ AB เป็นความสูงเอียง, AC เป็นส่วนสูง
BC เป็นความยาวครึ่งหนึ่งของด้านฐานยาว คือ 14 ÷ 2 = 7 นิ้ว ตามทฤษฎีปีทาโกรัส ในรูปสามเหลี่ยมมุมฉาก ABC
AC² + 7² = 25²
AC² = 625 – 49
AC² = 576
AC = 24
เพราะฉะนั้น ส่วนสูงยาว 24 นิ้ว

ขั้นที่ 2 หาปริมาตร
สูตรของปริมาตรพีระมิด = ¹/₃ × พื้นที่ฐาน × สูง
ได้ปริมาตรของพีระมิดนี้ = ¹/₃ × ( ด้าน × ด้าน ) × สูง
= ¹/₃ × ( 14 × 14 ) × 24
= 14 × 14 × 8
= 1,568 ลูกบาศก์เซนติเมตร
ตอบ 1,568 ลบ.ซม.

ปริซึม

รูปเรขาคณิตสามมิติที่มีหน้าตัดหัวท้าย (ฐาน) เป็นรูปเหลี่ยม ที่เท่ากันทุกประการ ด้านข้างแต่ละด้าน เป็นรูปสี่เหลี่ยมด้านขนาน.

1. การเรียกชื่อปริซึม
ปริซึมมีหลายลักษณะขึ้นอยู่กับหน้าตัดของรูปนั้นๆ การเรียกชื่อปริซึมนิยมเรียกชื่อตามลักษณะรูปเหลี่ยมของฐาน

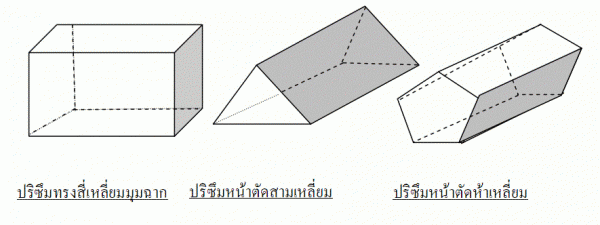
2. ส่วนประกอบของปริซึม

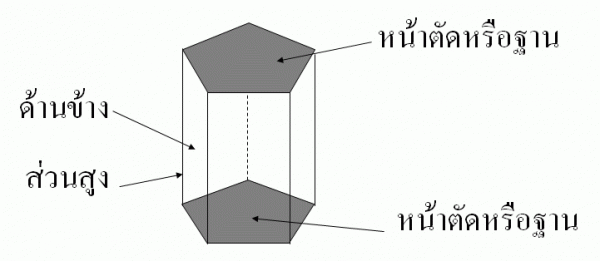
3. พื้นที่ผิวของปริซึม

          3.1) พื้นที่ผิวข้าง

พื้นที่ผิวข้างของปริซึม = ความยาวเส้นรอบฐาน × ความสูง

          3.2) พื้นที่ผิว

พื้นที่ผิวทั้งหมดของปริซึม = พื้นที่ผิวข้าง + พื้นที่หน้าตัดหัวท้าย

4. ปริมาตรของปริซึม

ปริมาตรของปริซึม = พื้นที่ฐาน × สูง

ตัวอย่างโจทย์

Ex.1

จงหาพื้นที่ผิวของแท่งปริซึมสามเหลี่ยมนี้

วิธีทำ

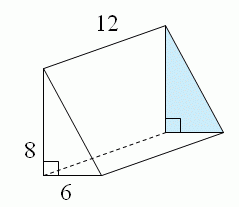
จากสูตร

พื้นทีฺ่ผิวทั้งหมดของปริซึม = พื้นที่ผิวข้าง + พื้นที่หน้าตัดหัวท้าย

ขั้นที่ 1 หาพื้นที่ผิวข้าง
จากสูตร พื้นที่ผิวข้างปริซึม = ความยาวรอบฐาน × ความสูง
จาก ทบ.ปีกาโกรัส เมื่อพิจารณาที่หน้าตัดแล้ว
จะได้ว่า ความยาวของหน้าตัด ด้านที่โจทย์ยังไม่ได้กำหนด ยาว = 10 หน่วย
ดังนั้น พื้นที่ผิวข้างปริซึม = ( 6 + 8 + 10 ) × 12
= 288 ตารางหน่วย

ขั้นที่ 2 หาพื้นที่หน้าตัดหัวท้าย
พื้นที่หน้าตัดหัวท้าย = 2 × พื้นที่ฐานสามเหลี่ยม
= 2 × (½ × ฐาน × สูง)
= 1 × 6 × 8
= 48
ดังนั้น พื้นที่หน้าัตัดหัวท้าย = 48 ตารางหน่วย

ขั้นที่ 3 หาพื้นที่่ผิวทั้งหมด
พื้นทีฺ่ผิวทั้งหมดของปริซึม = พื้นที่ผิวข้าง + พื้นที่หน้าตัดหัวท้าย
= 288 + 48
= 336 ตารางหน่วย
ตอบ 336 ตารางหน่วย

วิธีทำ เนื่องจากฐานเป็นรูปหกเหลี่ยมด้านเท่า
ดังนั้น เส้นรอบรูป = 4 × 6
= 24 นิ้ว

พื้นที่่ผิวข้างของปริซึม = ความยาวรอบฐาน × สูง
= 24 × 8
= 192 ตารางนิ้ว
(สูตรพื้นที่หกเหลี่ยมด้านเท่ามุมเท่า = ^3√3/₂ × ด้าน²)
พื้นที่ฐานรูปหกเหลี่ยมด้านเท่าุมุมเท่า = ^3√3/₂ × 4²
= 24√3 ตารางนิ้ว
พื้นที่ผิวของปริซึมนี้ = พื้่นที่ผิวข้าง + 2×(พื้นที่ฐาน)
= 192 + 2(24√3)
= 192 + 48√3
ตอบ 192 + 48√3 ตารางนิ้ว

Ex.3 จงหาปริมาตรของปริซึมสี่เหลี่ยมคางหมูนี้

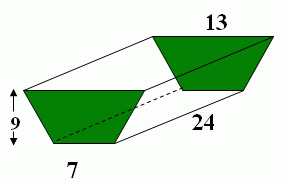
วิธีทำ สูตร พื้นที่ฐานปริซึมสี่เหลี่ยมคางหมู = 1/2 × ผลบวกของด้านคู่ขนาน × สูง
= 1/2 × (7 + 13) × 9
= 90 ตารางหน่วย

สูตร ปริมาตรปริซึม = พื้นที่ฐาน × สูง
= 90 × 24
= 2,160 ลูกบาศก์หน่วย
ตอบ 2,160 ลูกบาศก์หน่วย

ทรงกลม

รูปเรขาคณิตสามมิติที่มีผิวโคงเรียบ และจุดทุกจุดบนผิวโคงอยู่ห่างจากจุดคงที่จุดหนึ่งเป็นระยะทางเท่ากัน

จุดคงที่นั้นเรียกว่า จุดศูนย์กลางของทรงกลม และระยะทางที่เท่ากันนั้นเรียกว่า รัศมีของทรงกลม

1. ส่วนประกอบของทรงกลม

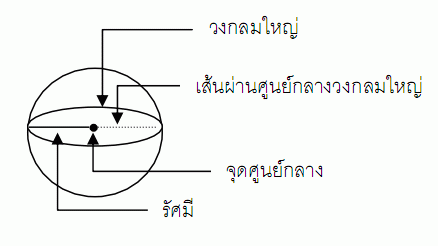
2. พื้นที่ผิวของทรงกลม

พื้นที่ผิวของทรงกลม = 4¶r²

3. ปริมาตรของทรงกลม

ปริมาตรของทรงกลม = ⁴/₃¶r³

เมื่อ r แทน รัศมีของวงกลม

ตัวอย่างโจทย์

Ex.1 ขันครึ่งทรงกลม วัดเส้นผ่านศูนย์กลางภายนอกปากขันได้ยาว 14 นิ้ว ขันใบนี้มีพื้นที่ผิวภายนอกเท่าไร

วิํธีทำ ขันมีรัศมี 7 นิ้ว
พื้นที่ผิวครึ่งทรงกลม = 2¶r²
= 2 × ²²/₇ × 7 × 7
= 308 ตารางนิ้ว
ดังนั้น ขันใบนี้มีพื้นที่ผิวภายนอกเท่ากับ 308 ตารางนิ้ว
ตอบ 308 ตารางนิ้ว