ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได (Step Function)

ฟังก์ชันขั้นบันได หมายถึงฟังก์ชันที่มีโดเมนเป็นสับเซตของเซตของจำนวนจริงและมีค่าของฟังก์ชันเป็นค่าคงตัวเป็นช่วงๆ

มากกว่าสองช่วงกราฟของฟังก์ชันนี้มีลักษณะคล้ายขั้น  บันได

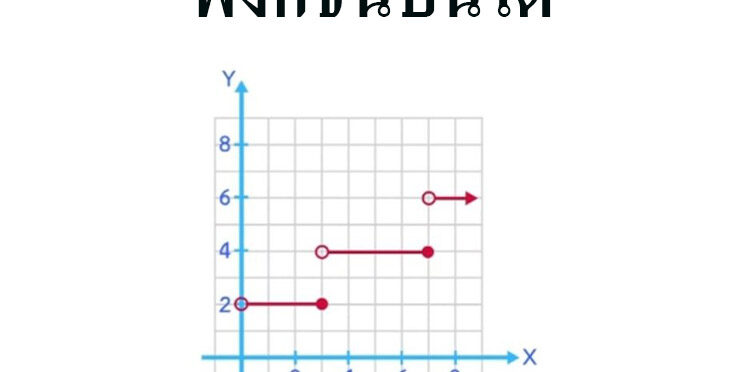
กราฟของฟังก์ชันนี้จะมีรูปร่างคล้ายขั้นบันได

ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได หมายถึง ฟังก์ชันที่มีโดเมนเป็นสับเซตของจำนวนจริง และมีค่าของฟังก์ชันเป็นค่าคงตัวเป็นช่วงๆ มากกว่าสองช่วง กราฟของฟังก์ชันนี้มีลักษณะคล้ายขั้นบันได

ตัวอย่างของฟังก์ชันขั้นบันไดที่พบเห็นในชีวิตประจำวัน ได้แก่ อัตราค่าบริการไปรษณียภัณฑ์ประเภทต่างๆ เช่น จดหมาย พัสดุไปรษณีย์ฟังก์ชันขั้นบันไดหมายถึง ฟังก์ชันที่มิโดเมนเป็นสับเซตของเซตของจำนวนจริงและมิค่าของฟังก์ชันเป็น ค่าคงตัวเป็นช่วงๆ มากกว่าสองช่วง กราฟของฟังก์ชันนี้มิลักษณะคล้ายขั้นบัน ได ตัวอย่างของฟังก์ชันขั้นบัน ใดที่พบเห็น ในชีวิตประ จำวัน ได้แก่อัตราค่าบริการไปรษณิยภัณฑ์ต่างๆ   เป็นต้น

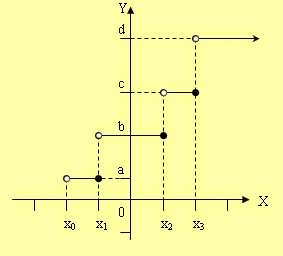
นิยาม

ฟังก์ชัน f : R → R จะเรียกว่าฟังก์ชันขั้นบันได ถ้าฟังก์ชัน fสามารถเขียนให้อยู่ในรูปแบบนี้ได้

สำหรับทุกจำนวนจริง x

เมื่อ n ≥ 0, α_i เป็นจำนวนจริง (ค่าคงตัว), A_i คือช่วงต่าง ๆ และ χ_A คือฟังก์ชันบ่งชี้

(indicator function) ของช่วง Aนั่นคือ

ในนิยามเช่นนี้ ช่วง A_i ต่าง ๆ จะต้องมีสมบัติที่สมมติขึ้นสองประการดังนี้

1. ช่วงต่าง ๆ จะต้องไม่มีส่วนร่วมต่อกัน นั่นคือ A_i ∩ A_j = ∅ โดยที่ i ≠ j
2. ยูเนียนของช่วงทุกช่วง คือเซตจำนวนจริงทั้งเซต นั่นคือ ∪_i A_i = R

ในกรณีที่สมบัติของฟังก์ชันเริ่มต้นไม่เป็นไปตามข้อสันนิษฐาน เช่นช่วงซ้อนกัน หรือยูเนียนแล้วแต่ไม่ครบเซต

จำนวนจริง เราอาจเลือกช่วงใหม่ที่เทียบเท่าอันทำให้มีสมบัติดังกล่าวได้ ตัวอย่างเช่น กำหนดให้ฟังก์ชันขั้นบันไดนี้

สามารถเขียนใหม่ได้เป็น

สมบัติ

ผลรวมและผลคูณของฟังก์ชันขั้นบันไดสองฟังก์ชัน จะให้ผลเป็นฟังก์ชันขั้นบันไดอีกฟังก์ชันหนึ่ง

และผลคูณของฟังก์ชันขั้นบันไดกับจำนวนคงตัวก็ยังคงเป็นฟังก์ชันขั้นบันได จากกรณีทั้งสองทำให้

ฟังก์ชันขั้นบันไดก่อร่างพีชคณิตขึ้นมาเหนือจำนวนจริง
ฟังก์ชันขั้นบันไดมีจำนวนช่วงเป็นจำนวนจำกัดเท่านั้น ถ้าช่วง A_i ต่าง ๆ

ซึ่ง i = 0, 1, …, n ตามนิยามข้างต้นไม่ทับซ้อนซึ่งกันและกัน และยูเนียนของช่วงทั้งหมดเป็นจำนวนจริง

จะได้ว่า f (x) = α_i สำหรับทุกค่าของ x ∈ A_i
ปริพันธ์เลอเบกของฟังก์ชันขั้นบันได  คือ

เมื่อ  คือความยาวของช่วง A และในกรณีนี้เราสมมติว่าช่วง A_i ทั้งหมดมีความยาวจำกัด

ข้อเท็จจริงคือความเท่ากันนี้สามารถใช้เป็นขั้นตอนแรกในการหาปริพันธ์เลอเบก ^[1]

สมบัติ

ผลรวมและผลคูณของฟังก์ชันขั้นบันไดสองฟังก์ชัน จะให้ผลเป็นฟังก์ชันขั้นบันไดอีกฟังก์ชันหนึ่ง

และผลคูณของฟังก์ชันขั้นบันไดกับจำนวนคงตัวก็ยังคงเป็นฟังก์ชันขั้นบันได จากกรณีทั้งสองทำให้ฟังก์ชันขั้นบันไดก่อร่าง

พีชคณิตขึ้นมาเหนือจำนวนจริงฟังก์ชันขั้นบันไดมีจำนวนช่วงเป็นจำนวนจำกัดเท่านั้น ถ้าช่วง A_i ต่าง ๆ ซึ่ง i = 0, 1, …, n

ตามนิยามข้างต้นไม่ทับซ้อนซึ่งกันและกัน และยูเนียนของช่วงทั้งหมดเป็นจำนวนจริง

จะได้ว่า f (x) = α_i สำหรับทุกค่าของ x ∈ A_iปริพันธ์เลอเบกของฟังก์ชันขั้นบันได  คือ  เมื่อ

คือความยาวของช่วง A และในกรณีนี้เราสมมติว่าช่วง A_i ทั้งหมดมีความยาวจำกัด

ข้อเท็จจริงคือความเท่ากันนี้สามารถใช้เป็นขั้นตอนแรกในการหาปริพันธ์เลอเบก