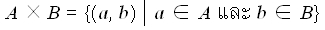ฟังก์ชันคอมโพสิท (ฟังก์ชันประกอบ)-คณิตศาสตร์ออนไลน์

ฟังก์ชันคอมโพสิท (ฟังก์ชันประกอบ)

เป็นการกระทำกันระหว่างฟังก์ชันตั้งแต่ 2 ฟังก์ชันขึ้นไป

ให้  f และ g  เป็นฟังก์ชัน  สำหรับฟังก์ชันที่เป็นเซตแบบแจกแจงเช่น

f = {(1,3),(2,4),(3,5)}

g = {(5,1),(3,2),(4,3)}

เราสามารถสร้างฟังก์ชันขึ้นมาใหม่ เรียกว่า gof (จีโอเอฟ) แต่ผมมักจะเรียกไปเลยว่า ก็อฟ

gof  เป็นฟังก์ชันจาก f ไปยัง g

จะได้       gof  = {(1,2),(2,4),(3,1)}

(gof)(1) = g(f(1)) = g(3) = 2

(gof)(2) = g(f(2)) = g(4) = 3

(gof)(3) = g(f(3)) = g(5) = 1

นิยาม ให้ f และ g เป็นฟังก์ชัน และ R _f ∩ D_g    ฟังก์ชันคอมโพสิทของ f และ g
เขียนแทนด้วย gof  กำหนด (gof)(x) = g(f(x))  ซึ่ง f(x) ∈ D_g

ตัวอย่างที่ 1  กำหนด f = {(1,2),(3,4),(5,6),(7,8)}

g = {(2,a),(4,b),(7,c),(8,d)}

จงหา (gof)(1) , (gof)(3) , (gof)(7)  พร้อมทั้งหา gof และ  fog

วิธีทำ   gof เป็นฟังก์ชัน จาก f ไป g

R _f   = {2,4,6,8} ,  D_g = {2,4,7,8}

R _f ∩ D_g  = {2,4,8}  ≠ Ø แสดงว่าหา gof ได้

(gof)(1) = g(f(1)) = g(2) = a

(gof)(3) = g(f(3)) = g(4) = b

(gof)(7) = g(f(7)) = g(8) = d

ดังนั้นจะได้  gof = {(1,a),(3,b),(7,d)}

fog  เป็นฟังก์ชันจาก g ไป f

R_g  =  {a,b,c,d} ,  D_f  =   {1,3,5,7}

R_g  ∩  D_f   = Ø

แสดงว่าหา fog   ไม่ได้

ตัวอย่างที่ 2  กำหนดให้ f(x) = 3x-5 , g(x) = 1/x-3

จงหา  gof , fog , (gof)(3) , (fog)(2)

วิธีทำ  1.) หา gof

R _f  =  R
D_g   =  R – {3}

R _f ∩ D_g  ≠ Ø แสดงว่าหา gof ได้

(gof)(x) = g(f(x))

= g(3x-5)

=  1/(3x-5)-3  = 1/3x-8

ดังนั้น gof = {(x,y) | y = 1/3x-8}

(gof)(3) = g(f(3)) = g(4) = 1

2.)  หา  fog

R_g  ≠  0

 D_f  =  R

R_g  ∩  D_f   ≠ Ø  แสดงว่าหา fog ได้

(fog)(x) = f(g(x)) = f(1/x-3)

= 3(1/x-3)-5 = (3/x-3)-5

(fog)(x) = 18-5x/x-3

fog   = {(x,y) |  y = 18-5x/x-3}
(fog)(2) = 18-5(2)/2-3 = 18-10/-1

= -8

ฟังก์ชันจากเซตหนึ่งไปยังอีกเซตหนึ่ง

ฟังก์ชันจาก A ไปทั่วถึง B

สัญลักษณ์   f เป็นฟังก์ชันจาก A ไป B จะเขียนแทนด้วย f : A→B  หรือ 
f : A→B อ่านว่า f เป็นฟังก์ชันจาก A ไปทั่วถึง B

ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B

ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไปทั่วถึง B

ฟังก์ชันเชิงเส้น (Linear Funtion)

ฟังก์ชันพหุนาม (Polynomial Function)

ฟังก์ชันขั้นบันได (Step Function)

ฟังก์ชันเอกซโพเนนเชียล (Exponential Function)

ฟังก์ชันลอการิทึม (Logarithm Function)

ฟังก์ชันตรีโกณมิติ (Trigonometry Function)

ฟังก์ชันค่าสัมบูรณ์ (Absolute Value Function)

คู่อันดับและผลคูณคาร์ทีเซียน

คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง

(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d

ผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B

สัญลักษณ์      ผลคูณคาร์ทีเซียนของเซต A และเซต B เขียนแทนด้วย A x B
หรือ เขียนในรูปเซตแบบบอกเงื่อนไขจะได้ว่า