ฟังก์ชันเลขชี้กำลังและฟังก์ชันลอการิทึม (คณิตศาสตร์เพิ่มเติม ม.4 )
ฟังก์ชันเลขชี้กำลัง (exponential function)
สมบัติที่สำคัญของฟังก์ชันเอกซ์โพเนนเชียล
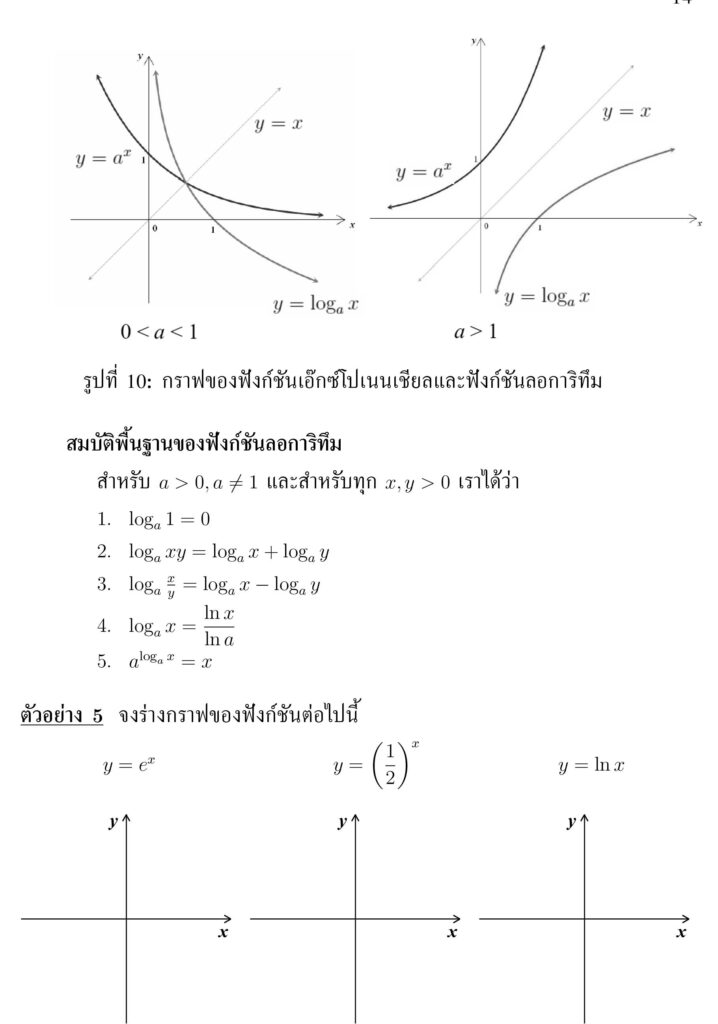
- เมื่อ a > 1 ฟังก์ชัน y = ax จะเป็นฟังก์ชันเพิ่ม และเมื่อ 0 < a < 1 ฟังก์ชัน y = ax จะเป็นฟังก์ชันลด
- ไม่มีค่าสูงสุดและค่าต่ำสุดของฟังก์ชัน
- กราฟของฟังก์ชันจะผ่านจุด (0, 1) และจะอยู่เหนือแกน X เสมอ
- โดเมนของฟังก์ชันเป็นจำนวนจริง (R) และเรนจ์ของฟังก์ชันเป็นจำนวนจริงบวก
- เมื่อ a มีค่ามาก ๆ กราฟของฟังก์ชันจะเรียวยาว
- แกน y จะเป็นแกนสมมาตรของกราฟของฟังก์ชัน y = ax และ y = (1/2)x
- กราฟของฟังก์ชันเอกซ์โพเนนเชียลบนระนาบ X’Y’ มีจุดกำเนิดที่ (h,k) เทียบกับระนาบ XY มีจุดกำเนิดที่ (0, 0) จะมีสมการเป็น y- k = ax-h
- ax = ay ก็ต่อเมื่อ x = y
- ถ้า ax > ay แล้ว x > y เมื่อ a > 1
- ถ้า ax > ay แล้ว x < y เมื่อ 0 < a < 1