ฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึม
ฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึม : เรื่อง การประยุกต์ของฟังก์ชันเอกซ์โพเนนเชียล ระดับชั้นมัธยมศึกษาปีที่ 4 ผลิตขึ้นเพื่อให้ครูในโรงเรียนทั่วประเทศได้ใช้ประกอบการสอนวิชาคณิตศาสตร์โดยใช้เครื่องคำนวณวิทยาศาสตร์ ให้นักเรียนนำความรู้เรื่องฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึมไปใช้ในการแก้ปัญหาต่างๆ รวมถึงมีเจตคติที่ดีต่อคณิตศาสตร์มากขึ้น
- เลขยกกำลัง จะกล่าวถึงพื้นฐานของฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึม ซึ่งได้แก่ เลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนตรรกยะ และกล่าวถึงสมบัติการดำเนินการของเลขยกกำลังรวมไปถึงรากและจำนวนจริงในรูปกรณฑ์
- ฟังก์ชันเอกซ์โพเนนเชียล จะกล่าวถึงฟังก์ชันของเลขยกกำลังและกราฟ รวมไปถึงลักษณะของฟังก์ชันเอกซ์โพเนนเชียล
- สมการและอสมการเอกซ์โพเนนเชียล จะกล่าวถึงการแก้สมการและอสมการในรูปของเลขยกกำลัง โดยอาศัยสมบัติการดำเนินการของเลขยกกำลัง
- ฟังก์ชันลอการิทึม หรือฟังก์ชันผกผันของฟังก์ชันเอกซ์โพเนนเชียล จะกล่าวถึงลักษณะของฟังก์ชันลอการิทึมและกราฟ รวมไปถึงลักษณะของฟังก์ชันลอการิทึม
- สมบัติของลอการิทึม จะกล่าวถึงสมบัติของลอการิทึม โดยอาศัยสมบัติของเอกซ์โพเนนเชียล
- สมการและอสมการลอการิทึม จะกล่าวถึงการแก้สมการและอสมการในรูปของลอการิทึมโดยอาศัยสมบัติ
- การประยุกต์ของฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึม เป็นการนำฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึมไปประยุกต์ใช้ในชีวิตประจำวัน
ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม
- เลขยกกำลัง
- การเปรียบเทียบเลขยกกำลัง
- สมการรากที่สอง
- รูปแบบรูทไม่รู้จบ
- ฟังก์ชันเอกซ์โพเนนเชียล
- กราฟของฟังก์ชันเอกซ์โพเนนเชียล และการแปลงกราฟ
- สมการเอกซ์โพเนนเชียล
- อสมการเอกซ์โพเนนเชียล
- ฟังก์ชันลอการิทึม
- กราฟของฟังก์ชันลอการิทึม และการแปลงกราฟ
- สมบัติของฟังก์ชันลอการิทึม
- การเปรียบเทียบค่าลอการิทึม
- แมนทิสซา และคาแรกเทอริสติก
- สมการลอการิทึม
- อสมการลอการิทึม
ฟังก์ชันเอ็กโปเนนเชียลและลอการิทึม-คณิตศาสตร์
กฎของเลขยกกำลัง
ถ้า a,b เป็นจำนวนจริงใดๆจะได้
1. am+ an = am+n
2. (ab)n = anbn
3. (am)n = amn
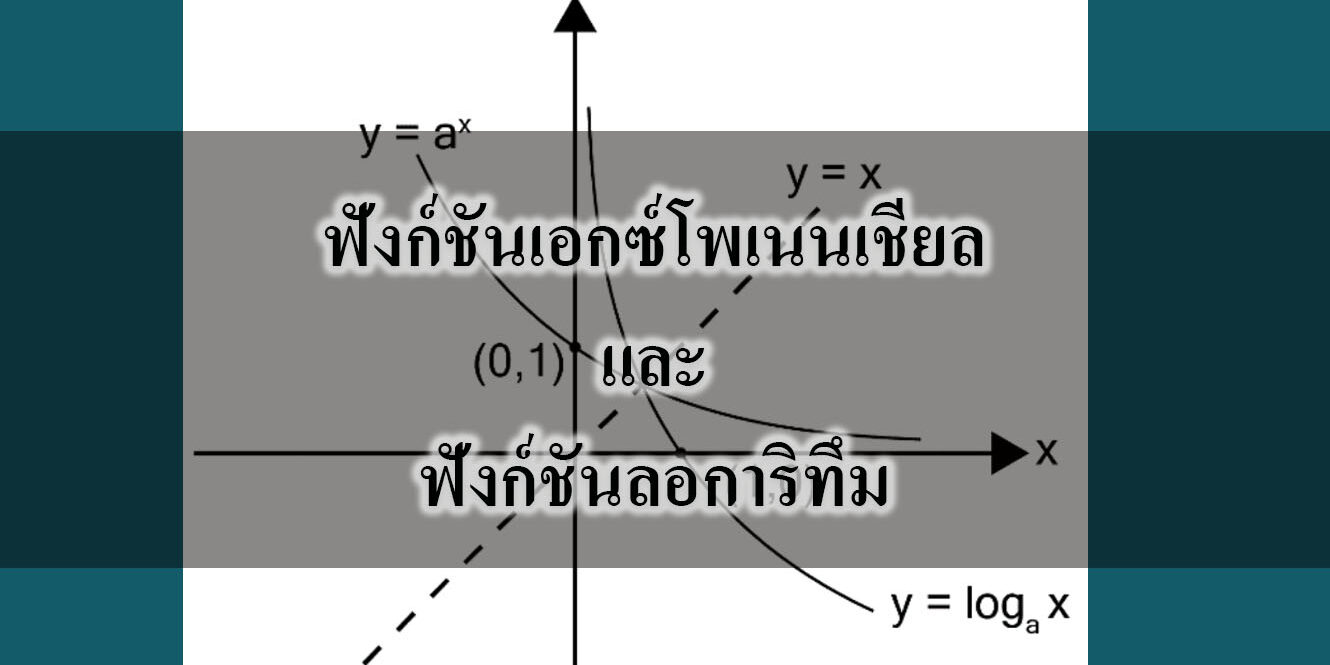
f = { (x,y) | R x R+ | y = ax ; a > 0 และ a น 1 } เรียกว่า ฟังก์ชันเอกซ์โปเนนเชียล จาก y = ax , a > 0, a น 1 จะได้ x ฮ R และ y ฮ R+ นั่นคือ โดเมนเป็นเซตของจำนวนจริง และเรนจ์เป็นเซตของจำนวนจริงบวก
1. ถ้า a > 1 ฟังก์ชันเอกโพเนนเชียลเป็นฟังก์ชันเพิ่ม
2. ถ้า 0 < a < 1 ฟังก์ชันเอกโพเนนเชียลเป็นฟังก์ชันลด
3. สมบัติที่สำคัญคือ ex = ey ก็ต่อเมื่อ x = y ส่วนสมบัติอื่นๆมีเช่นเดียวกับเลขยกกำลัง
การแก้สมการเอ็กโปเนนเชียล
การแก้สมการเอกโพเนนเชียลที่มักพบอยู่บ่อยๆมี 4 วิธี คือ
1. ทำให้ฐานเท่ากัน คือทำให้ ap(x) = aq(x) แล้วสรุปว่า p(x) = q(x)
2. ทำให้กำลังเหมือนกันแต่ฐานต่างกัน คือ ap(x) = bq(x) แล้วสรุปได้ว่า p(x) = 0
3.ทำให้เป็นเลขจำนวนเดียวยกกำลังแล้วมีค่าเท่ากับ 1 คือทำเป็น (abc)u = 1 แล้วสรุปว่า u = 0
ข้อสังเกต
- ไม่ว่า x จะเป็นจำนวนจริงใด ๆ ก็ตาม 1x ก็ยังคงเท่ากับ 1 เสมอ ดังนั้นจึงไม่น่าสนใจ เนื่องจาก เราทราบว่ามันเป็นอะไรแน่ ๆ อยู่แล้ว
- เรายังไม่ทราบนะว่า เลขยกกำลังที่มีฐานเป็นจำนวนจริงบวกยกเว้น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ แสดงว่าเราจะต้องสนใจศึกษาเลขยกกำลังลักษณะนี้เป็นพิเศษ ซึ่งจะกล่าวถึงใน เรื่องฟังก์ชันเอกซ์โพเนนเชียลดังนี้
ข้อกำหนด (ฟังก์ชันเอกซ์โพเนนเชียล)
ฟังก์ชันเอกซ์โพเนนเชียล คือ f = { (x, y) Î R ´ R+ / y = ax , a > 0, a ¹ 1 }
ข้อตกลง ในหนังสือคณิตศาสตร์บางเล่มให้ข้อกำหนดของฟังก์ชันเอกซ์โพเนนเชียล เป็นฟังก์ชันที่อยู่ในรูป f(x) = kax เมื่อ k เป็นค่าคงตัวที่ไม่ใช่ 0 และ a เป็นจำนวนจริงบวกที่ไม่เป็น 1 แต่ในหลักสูตรมัธยมศึกษาตอนปลายนี้ จะถือว่าฟังก์ชันเอกซ์โพเนนเชียลจะอยู่ในรูป f(x) = ax เมื่อ a เป็น จำนวนจริงบวกที่ไม่เป็น 1 เท่านั้น
ข้อสังเกต จากข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล
- f(x) = 1x เป็นฟังก์ชันคงตัวเนื่องจาก 1x = 1 ดังนั้นในข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล จึงไม่สนใจ ฐาน (a) ที่เป็น 1
- f(x) = 1x ไม่เป็นฟังก์ชันเอ็กซ์โพเนนเชียล เนื่องจาก f(x) = 1x เป็นฟังก์ชันคงตัว
- จากเงื่อนไขที่ว่า y = ax, a > 0, a ¹ 1 ทำให้เราทราบได้เลยว่าฐาน (a) มีอยู่ 2 ลักษณะ คือ 0 < a < 1 กับ a > 1
- ฟังก์ชันเอกซ์โพเนนเชียลจะมีอยู่ 2 ชนิด โดยขึ้นอยู่กับลักษณะของฐาน (a) ดังนี้
ชนิดที่ 1 y = ax, 0 < a < 1
ชนิดที่ 2 y = ax, a > 1
การแก้อสมการเอกซ์โพเนนเชียล
กลุ่มที่ 1 ฐานเหมือนกันเลขชี้กำลังต่างกัน
| 1. เมื่อ | a > 1 | จะได้ว่า อสมการของเลขชี้กำลังจะคล้อยตามอสมการของเลขยกกำลัง |
|
เช่น |
ax > ay | จะได้ว่า x > y |
| ax < ay | จะได้ว่า x < y | |
| 2. เมื่อ | 0 < a < 1 | จะได้ว่า อสมการของเลขชี้กำลังจะตรงข้ามกับอสมการของเลขชี้กำลัง |
| เช่น | ax > ay | จะได้ว่า x < y |
| ax < ay | จะได้ว่า x > y |
กลุ่มที่ 2 ฐานต่างกันเลขชี้กำลังเหมือนกัน
| 1. | ถ้าอสมการของเลขยกกำลังคล้อยตามอสมการของเลขฐานจะได้ว่าเลขชี้กำลัง < 0 |
| เช่น a < b , ax < bx จะได้ว่า x > 0 | |
| a > b , ax > bx จะได้ว่า x > 0 | |
| 2. | ถ้าอสมการของเลขยกกำลังตรงข้ามกับอสมการของเลขฐานจะได้ว่าเลขชี้กำลัง < 0 |
| เช่น a > b , ax < bx จะได้ว่า x < 0 | |
| a < b , ax > bx จะได้ว่า x < 0 | |
| y = loga x มีความหมายว่า x = ay | |
| ถ้า a = 10 เรียกว่า ลอการิทึมสามัญ เขียนแทนด้วย log x ถ้า a = e ป 2.71828 เรียกว่า ลอการิทึมธรรมชาติ เขียนแทนด้วยสัญลักษณ์ ln x ( คือ loge x ) โดเมนของฟังก์ชันลอการิทึมเป็นเซตของจำนวนจริงบวก เรนจ์ของฟังก์ชันลอการิทึมเป็นเซตของจำนวนจริง |
| สมบัติที่สำคัญ | |||
| 1. 2. |
loga x loga xy |
= = |
loga y ก็ต่อเมื่อ x = y loga x + loga y |
| 3. 4. |
loga(x/y) loga xy |
= = |
loga x + loga y yloga x + loga |
| 5. | logaa | = | 1 |
| 6. | loga1 | = | 0 |
| 7. | ln 1 | = | log 1 = 0 |
| 8. | ln e | = | 1, log 10 =1 |
| 9. | eln x | = | x , 10log x = x |
| 10. | ln ex | = | x , log 10x = x |
| 13. | ax | = | ex ln a |
การหาค่า log x เขียน x = A ด 10n เมื่อ 1 < A < 10 หาค่าของ log A จากตาราง แล้วจะได้
log x = n + log A
|
ตัวอย่าง log 5710 |
= log (5.71 ด 103) = 3 + log 5.71 = 3 + 0.7566 = 3.7566 |
การหาค่า x เมื่อทราบค่า log x เช่น log x = 7.8341 ค่า x ทำได้โดยการใช้เครื่องคิดเลขและการเปิดตาราง
1. เขียน log x = n + B เมื่อ 0 < B < 1 และ n เป็นจำนวนเต็ม
2. หาค่า y เมื่อ log y = B จากตารางแอนติลอการิทึมหรือตารางลอการิทึม (โดยดูย้อนกลับ) ได้ค่า y
แล้วจะได้ x = y ด 10n
การแก้สมการลอการิทึม การแก้สมการลอการิทึมมีรูปแบบที่พบกันบ่อยๆอยู่ 4 วิธี คือ
1. แยกตัวประกอบ เช่น (log 4 x)3-(log 4 x)2 – 2log 4 x = log 4 x (log 4 x – 2)( log 4 x + 1 ) = 0
2. เปลี่ยนรูป y = logax เป็น x = ay
3. ทำให้เป็นลอการิทึมฐานเดียวกันมีค่าเท่ากันคือทำให้ log a u = log a v แล้วสรุปว่า u = v
4. แปลงรูปสมการโดยใช้สมบัติของลอการิทึม
การแก้อสมการลอการิทึม อสมการลอการิทึมสามารถแก้ได้โดยใช้สมบัติต่อไปนี้คือ
1. กรณีที่ a > 0 จะได้ว่า logau > loga v ก็ต่อเมื่อ u > v
2. กรณีที่ 0 < a < 1 จะได้ว่า loga u > loga v ก็ต่อเมื่อ u < v
3. แปลงอสมการลอการิทึมให้อยู่ในรูปอสมการเอกซ์โพเนนเชียล เช่น
log3( x + 2 ) < 4 = x + 2 < 34