ภาคตัดกรวยเรื่อง – พาราโบลา โฟกัส ไดเรกตริกซ์ เลตัสเรกตัม
พาราโบลาคือเซตของจุดทุกจุดบนระนาบ ซึ่งอยู่ห่างจากเส้นตรงที่ เส้นหนึ่งบนระนาบและจุดคงที่จุดหนึ่ง
บนระนาบนอกเส้นตรงคงที่นั้น เป็น ระยะทางเท่ากับเสมอ
– จุดคงที่ เรียกว่า โฟกัส (focus) ของพาราโบลา
– เส้นตรงที่คงที่ คือเส้นบังคับ หรือเส้นไดเรกตริกซ์ (Directrix)
– เส้นตรงที่ลากผ่านจุดโฟกัส และตั้งฉากกับไดเรกตริกซ์คือแกน ของพาราโบลา หรือแกนสมมาตร(axis of symmetry)
– จุดที่แกนพาราโบลาตัดเส้นโค้งของพาราโบลาคือ จุดยอด (vertex) ของพาราโบลา
– ส่วนของเส้นตรงที่ลากผ่านจุดโฟกัส และตั้งฉากกับแกนของพาราโบลา โดยจุดปลายทั้งสองอยู่บนโค้ง
ของพาราโบลาเรียกว่า ลาตัสเรกตัม (Latus Recrum) รูปแบบสมการ มี 2 รูปแบบใหญ่ๆ คือ
1. สมการ y = ax² + bx + c
2. สมการ y = a(x –h)² + k
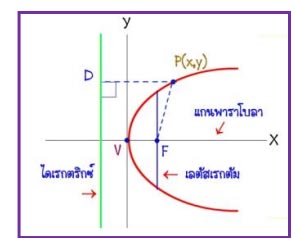
ถ้า P(x, y) บนจุดใดๆ บนกราฟของพาราโบลา จะได้ว่า |PF|= |PD|
1. สมการพาราโบลาที่มีจุดศูนย์กลางอยู่ที่จุด (0, 0)
1.1 เมื่อแกน x เป็นแกนสมมาตร
1.2 เมื่อแกน y เป็นแกนสมมาตร
2. สมการพาราโบลาที่มีจุดศูนย์กลางอยู่ที่จุด (h, k)
2.1 เมื่อแกนสมมาตรขนานกับแกน x
2.2 เมื่อแกนสมมาตรขนานกับแกน y
1. สมการพาราโบลาที่มีจุดศูนย์กลางอยู่ที่จุด (0, 0)
1.1 เมื่อแกน x เป็นแกนสมมาตร
สมการพาราโบลาที่มีจุดศูนย์กลางอยู่ที่จุด (0, 0) เมื่อแกน x เป็นแกนสมมาตร
ความสัมพันธ์ของกราฟ คือ{ (x,y) ∈ RΧR | y²= 4cx }
เป็นพาราโบลาที่มีแกนในแนวนอน แกน x หรือเส้นตรง y = 0







