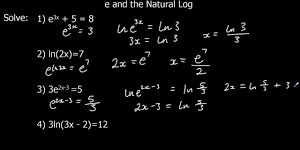มาติวเอกซ์โพเนนเชียล ลอการิทึม-เรื่องลอการิทึมธรรมชาติ (Natural logarithm)

เอกซ์โพเนนเชียล ลอการิทึม (Exponential Function) ระดับชั้น ม.5 เรื่อง ลอการิทึมแบบเนเปียร์ (Napierian logarithms)

 ลอการิทึมธรรมชาติ (Natural logarithm)

1. ลอการิทึมธรรมชาติ  หมายถึง  ลอการิทึมที่มีฐานเป็น e โดยที่ e เป็นสัญลักษณ์แทนจำนวนอตรรกยะจำนวนหนึ่งซึ่งมีค่าประมาณ 2.7182818

แสดงว่า  logex คือ  ลอการิทึมธรรมชาติ  นั่นเอง

ข้อกำหนด

1. ลอการิทึมธรรมชาติ หมายถึง  ลอการิทึมที่มีฐานเป็น e โดยที่ e เป็นสัญลักษณ์แทนจำนวนอตรรกยะจำนวนหนึ่งซึ่งมีค่าประมาณ 2.7182818

แสดงว่า  log_ex คือ  ลอการิทึมธรรมชาติ  นั่นเอง

2. การเขียนลอการิทึมของ x ฐาน e นิยมเขียน ln x แทน  log_ex
3. ”ลอการิทึมธรรมชาติ (Natural logarithms)” อาจถูกเรียกอีกอย่างหนึ่งว่า  “ลอการิทึมแบบเนเปียร์ (Napierian logarithms)

ข้อควรเน้น  ถ้าเราเจอ ln x อยากเปลี่ยนไปเป็น logex  แล้วคิดทำทุกอย่างเหมือนที่เคยคิดทำ log ทั่ว ๆ ไป

สิ่งที่ควรทราบ

1. เราอาจหาค่าลอการิทึมฐาน e โดยอาศัยลอการิทึมฐานสิบได้ดังนี้

จาก ln x = logex

ln x =

เราพบว่า loge = log 2.718 (e  2.718)

= 0.4343

ดังนั้น ln x =

หรือ ln x = (2.3026)  logx

การคำนวณค่าโดยประมาณโดยใช้ลอการิทึม

สำหรับการคำนวณที่เกี่ยวกับ  การคูณ  การหาร  และยกกำลัง  อาจอาศัยลอการิทึมช่วยในการคำนวณได้  โดยค่าที่คำนวณได้จะมีค่าโดยประมาณแต่ก็ใกล้เคียงกับค่าที่แท้จริง

ตัวอย่าง 1  จงหาค่าของ

วิธีทำ สมมุติให้ x =

log x = log

= log 0.0413 + log 43.2 – log 0.912

= log 4.13 x 10-2 + log 4.32 x 101 – log 9.12 x 10-1

= (0.6160 – 2) + (0.6355 + 1) – (0.9600 – 1)

= 0.2915

= log 1.96

แสดงว่า  x = 1.96

ดังนั้น = 1.96

สูตร ln

สูตร ln หรือลอการิทึมฐานธรรมชาติ คือ ฐาน e = ln = log x ฐาน e นั่งเอง

โดย log e ฐาน 10 มีค่าเท่ากับ 0.4343
1/0.4343  = 2.3026
log x ฐาน e = ln x
ln x = (2.3026)

สมบัติของลอการิทึมฐานธรรมชาติ (ln) มีดังนี้

1. ln MN = ln M + ln N
2. ln M/N = ln M – ln N
3. ln (M^p) = p ln M
4. ln 1 = 0, e^0 = 1
5. ln e= 1, e^1= 1
6. e ^lnx= x, x > 0 เพราะ lnx=lnx
7. ln (e^x) = x สำหรับทุกค่า x
8. ln (1/x) = -lnx

ตัวอย่างโจทย์เกี่ยวกับสูตร ln

1. กำหนดให้ ln x = 0 จงหาค่าของ x

ln x = 0

x = e ^ 0 =1

ดังนั้น x = 1