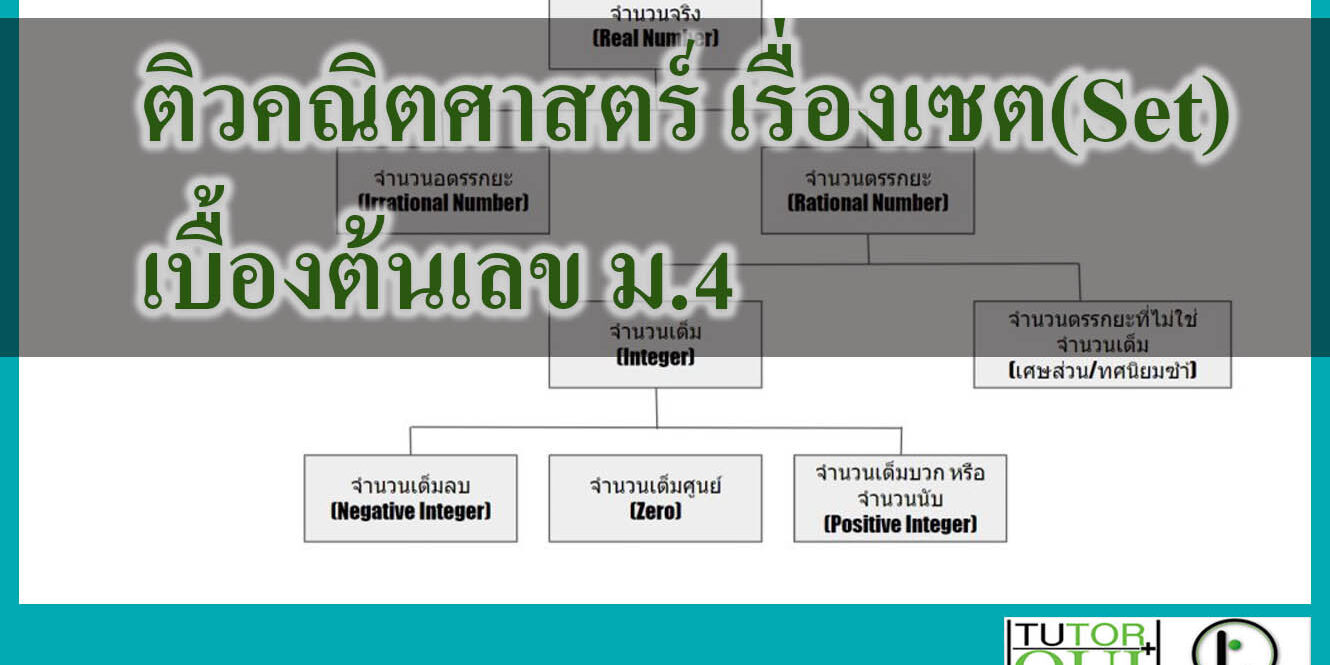
ระบบของ จำนวนจริง (Real Number) ม.4
จำนวนจริง ( Real Number )
จำนวนจริงชนิดต่าง ๆ
- จำนวนนับ
เซตของจำนวนนับเขียนได้ดังนี้ N = { 1 , 2 , 3 , 4 , … }
- จำนวนเต็ม เมื่อสังคมของมนุษย์เจริญมากขึ้น จนวนนับก็ไม่เพียงพอแก่การนำไปใช้ จึงได้มรการคิดจำนวนชนิดใหม่ขึ้นโดยการนำจำนวนนับ 2 จำนวนมาลบกัน ผลลัพธ์ที่ได้เรียกว่า “จำนวนเต็ม” ซึ่งแบ่งเป็น 3 อย่างคือ
1) จำนวนเต็มบวก เกิดจากการลบที่ตัวตั้งมีค่ามากกว่าตัวลบ
เซตของจำนวนเต็มบวกแทนด้วย I+ = { 1 , 2 , 3 , … }
2) จำนวนเต็มศูนย์ เกิดจากการลบที่ตัวตั้งเท่ากับตัวลบ
เซตของจำนวนเต็มศูนย์ = { 0 } มีสมาชิกตัวเดียว
3) จำนวนเต็มลบเกิดจากการลบที่ตัวตั้งมีค่าน้อยกว่าตัวลบ
เซตของจำนวนเต็มลบแทนด้วย I– = { -1 , -2 , -3 , … }
Note .::. จำนวนเต็ม = I = { … , -3 , -2 , -1 , 0 , 1 , 2 , 3 , … }
3. จำนวนตรรกยะ เกิดจากการนำจำนวนเต็ม 2 จำนวนมาหารกัน โดยที่ตัวหารไม่เท่ากับ 0 อาจกล่าวได้ว่าจำนวนตรรกยะคือ จำนวนที่เขียนในรูปเศษส่วนได้
เซตของจำนวนตรรกยะเขียนได้ดังนี้
Q = { | เป็นจำนวนเต็ม และ }
1) จำนวนตรรกยะมีทั้งที่เป็นบวก เป็นศูนย์ และเป็นลบ
2) จำนวนเต็มทุกจำนวนเป็นเป็นจำนวนตรรกยะด้วย เพราะเขียนในรูปเศษส่วนได้ เช่น
3) จำนวนที่เป็นทศนิยมรู้จบ กับจำนวนที่เป็นทศนิยมไม่รู้จบแบบซ้ำทุกจำนวนเป็นจำนวนตรกกยะ เพราะแปลงเป็นเศษส่วนได้ เช่น4. จำนวนอตรรกยะ
5. จำนวนจริง คือ เซตของจำนวนที่เกิดจากการนำเซตของจำนวนตรรกยะยูเนียนกับเซตของจำนวนอตรรกยะ
เขียนแทนด้วยเซต
จำนวนจริง(Real Number)
1. จำนวนอตรรกยะ หมายถึง จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือทศนิยมซ้ำได้ ตัวอย่างเช่น √2 , √3, √5, -√2, – √3, -√5 หรือ ¶ ซึ่งมีค่า 3.14159265…
2. จำนวนตรรกยะ หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็มหรือทศนิยมซ้ำได้ ตัวอย่างเช่น
เขียนแทนด้วย 0.5000…
เขียนแทนด้วย 0.2000…
• ระบบจำนวนตรรกยะ
จำนวนตรรกยะยังสามารถแบ่งเป็น 2 ประเภท คือ
1. จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม หมายถึง จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนหรือทศนิยมซ้ำได้ แต่ไม่เป็นจำนวนเต็ม ตัวอย่างเช่น
2. จำนวนเต็ม หมายถึง จำนวนที่เป็นสมาชิกของเซต I = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …} เมื่อกำหนดให้ I เป็นเซตของจำนวนเต็ม
• ระบบจำนวนเต็ม
จำนวนเต็มยังสามารถแบ่งได้อีกเป็น 3 ประเภทด้วยกัน
1. จำนวนเต็มลบ หมายถึง จำนวนที่เป็นสมาชิกของเซต I – โดยที่
I – = {…, -4, -3, -2, -1}
เมื่อ I – เป็นเซตของจำนวนเต็มลบ
2. จำนวนเต็มศูนย์ (0)
3. จำนวนเต็มบวก หมายถึง จำนวนที่เป็นสมาชิกของเซต I+ โดยที่
I+ = {1, 2, 3, 4, …}
เมื่อ I+ เป็นเซตของจำนวนเต็มบวก
จำนวนเต็มบวก เรียกได้อีกอย่างว่า “จำนวนนับ” ซึ่งเขียนแทนเซตของจำนวนนับได้ด้วยสัญลักษณ์ N โดยที่
N = I+ = {1, 2, 3, 4, …}
• ระบบจำนวนเชิงซ้อน
นอกจากระบบจำนวนจริงที่กล่าวมาข้างต้นแล้ว ยังมีจำนวนอีกประเภทหนึ่ง ซึ่งได้จากการแก้สมการต่อไปนี้
x2 = -1 ∴ x = √-1 = i
x2 = -2 ∴ x = √-2 = √2 i
x2 = -3 ∴ x = √-3 = √3 i
จะเห็นได้ว่า “ไม่สามารถจะหาจำนวนจริงใดที่ยกกำลังสองแล้วมีค่าเป็นลบ” เราเรียก √-1 หรือจำนวนอื่นๆ ในลักษณะนี้ว่า “จำนวนจินตภาพ”และเรียก i ว่า “หนึ่งหน่วยจินตภาพ” เขียนแทนด้วยสัญลักษณ์ i
ยูเนียนของเซตจำนวนจริงกับเซตจำนวนจินตภาพ คือ ” เซตจำนวนเชิงซ้อน ” (Complex numbers)
กำหนด a, b, c เป็นจำนวนจริงใดๆ
1. สมบัติการสะท้อน a = a
2. สมบัติการสมมาตร ถ้า a = b แล้ว b = a
3. สมบัติการถ่ายทอด ถ้า a = b และ b = c แล้ว a = c
4. สมบัติการบวกด้วยจำนวนที่เท่ากัน ถ้า a = b แล้ว a + c = b + c
5. สมบัติการคูณด้วยจำนวนที่เท่ากัน ถ้า a = b แล้ว ac = bc
• สมบัติการบวกในระบบจำนวนจริง
กำหนด a, b, c เป็นจำนวนจริงใดๆ
1. สมบัติปิดการบวก a + b เป็นจำนวนจริง
2. สมบัติการสลับที่ของการบวก a + b = b + c
3. สมบัติการเปลี่ยนกลุ่มการบวก a + ( b + c) = ( a + b ) + c
4. เอกลักษณ์การบวก 0 + a = a = a + 0
นั่นคือ ในระบบจำนวนจริงจะมี 0 เป็นเอกลักษณ์การบวก
5. อินเวอร์สการบวก a + ( -a ) = 0 = ( -a ) + a
นั่นคือ ในระบบจำนวนจริง จำนวน a จะมี -a เป็นอินเวอร์สของการบวก
สมบัติการคูณในระบบจำนวนจริง
กำหนดให้ a, b, c, เป็นจำนวนจริงใดๆ
1. สมบัติปิดการคูณ ab เป็นจำนวนจริง
2. สมบัติการสลับที่ของการคูณ ab = ba
3. สมบัติการเปลี่ยนกลุ่มของการคูณ a(bc) = (ab)c
4. เอกลักษณ์การคูณ 1 · a = a = a · 1
นั่นคือในระบบจำนวนจริง มี 1 เป็นเอกลักษณ์การคูณ
5. อินเวอร์สการคูณ a · a-1 = 1 = a · a-1, a ≠ 0
นั่นคือ ในระบบจำนวนจริง จำนวนจริง a จะมี a-1 เป็นอินเวอร์สการคูณ ยกเว้น 0
6. สมบัติการแจกแจง
a( b + c ) = ab + ac
( b + c )a = ba + ca
จากสมบัติของระบบจำนวนจริงที่ได้กล่าวไปแล้ว สามารถนำมาพิสูจน์เป็นทฤษฎีบทต่างๆ ได้ดังนี้
ทฤษฎีบทที่ 1 กฎการตัดออกสำหรับการบวก
เมื่อ a, b, c เป็นจำนวนจริงใดๆ
ถ้า a + c = b + c แล้ว a = b
ถ้า a + b = a + c แล้ว b = c
ทฤษฎีบทที่ 2 กฎการตัดออกสำหรับการคูณ
เมื่อ a, b, c เป็นจำนวนจริงใดๆ
ถ้า ac = bc และ c ≠ 0 แล้ว a = b
ถ้า ab = ac และ a ≠ 0 แล้ว b = c
ทฤษฎีบทที่ 3 เมื่อ a เป็นจำนวนจริงใดๆ
a · 0 = 0
0 · a = 0
ทฤษฎีบทที่ 4 เมื่อ a เป็นจำนวนจริงใดๆ
(-1)a = -a
a(-1) = -a
ทฤษฎีบทที่ 5 เมื่อ a, b เป็นจำนวนจริงใดๆ
ถ้า ab = 0 แล้ว a = 0 หรือ b = 0
ทฤษฎีบทที่ 6 เมื่อ a เป็นจำนวนจริงใดๆ
a(-b) = -ab
(-a)b = -ab
(-a)(-b) = ab
เราสามารถนิยามการลบและการหารจำนวนจริงได้โดยอาศัยสมบัติของการบวกและการคูณใน
ระบบจำนวนจริงที่ได้กล่าวไปแล้วข้างต้น
• การลบจำนวนจริง
บทนิยาม เมื่อ a, b เป็นจำนวนจริงใดๆ
a- b = a + (-b)
นั่นคือ a – b คือ ผลบวกของ a กับอินเวอร์สการบวกของ b
• การหารจำนวนจริง
บทนิยาม เมื่อ a, b เป็นจำนวนจริงใดๆ เมื่อ b ≠ 0
= a(b-1)
นั่นคือ คือ ผลคูณของ a กับอินเวอร์สการคูณของ b
การแก้สมการตัวแปรเดียว
บทนิยาม สมการพหุนามตัวแปรเดียว คือ สมการที่อยู่ในรูป
anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0 = 0
เมื่อ n เป็นจำนวนเต็มบวก และ an, an-1, an-2 ,…, a1, a0 เป็นจำนวนจริง ที่เป็นสัมประสิทธิ์ของพหุนาม โดยที่ an ≠ 0 เรียกสมการนี้ว่า “สมการพหุนามกำลัง n”
ตัวอย่างเช่น x3 – 2×2 + 3x -4 = 0
4×2 + 4x +1 = 0
2×4 -5×3 -x2 +3x -1 = 0
• การแ้ก้สมการพหุนามเมื่อ n > 2
สมการพหุนามกำลัง n ซึ่งอยู่ในรูป anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0 = 0 เมื่อ n > 2 และ an, an-1, an-2 ,…, a1, a0 เป็นจำนวนจริง โดยที่ an ≠ 0 จะสามารถหาคำตอบของสมการพหุนามกำลัง n นี้ได้โดยใช้ทฤษฎีบทเศษเหลือช่วยในการแยกตัวประกอบ
ทฤษฎีบทเศษเหลือ
เมื่อ f(x) = anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0
โดย n > 2 และ an, an-1, an-2 ,…, a1, a0 เป็นจำนวนจริง และ an ≠ 0
ถ้าหารพหุนาม f(x) ด้วยพหุนาม x – c เมื่อ c เป็นค่าคงตัวใดๆแล้ว เศษของ
การหารจะมีค่าเท่ากับ f(c)
นั่นคือ เศษของ คือ f(c)
ทฤษฎีบทตัวประกอบ
เมื่อ f(x) = anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0
โดย n > 2 และ an, an-1, an-2 ,…, a1, a0 เป็นจำนวนจริง และ an ≠ 0
พหุนาม f(x) นี้จะมี x – c เป็นตัวประกอบ ก็ต่อเมื่อ f(c) = 0
ถ้า f(c) = 0 แล้วเศษของ คือ 0
แสดงว่า x – c หาร f(c) ได้ลงตัว
นั่นคือ x – c เป็นตัวประกอบของ f(x)
ทฤษฎีบทตัวประกอบจำนวนตรรกยะ
เมื่อ f(x) = anxn + an-1xn-1 + an-2xn-2 + … + a1x + a0
โดย n > 2 และ an, an-1, an-2 ,…, a1, a0 เป็นจำนวนจริง และ an ≠ 0
ถ้า x -เป็นตัวประกอบของพหุนามของ f(x) โดยที่ m และ k เป็นจำนวนเต็ม
สมบัติของการไม่เท่ากัน
บทนิยาม a < b หมายถึง a น้อยกว่า b
a > b หมายถึง a มากกว่า b
• สมบัติของการไม่เท่ากัน
กำหนดให้ a, b, c เป็นจำนวนจริงใดๆ
1. สมบัติการถ่ายทอด ถ้า a > b และ b > c แล้ว a > c
2. สมบัติการบวกด้วยจำนวนที่เท่ากัน ถ้า a > b แล้ว a + c > b+ c
3. จำนวนจริงบวกและจำนวนจริงลบ
a เป็นจำนวนจริงบวก ก็ต่อเมื่อ a > 0
a เป็นจำนวนจริงลบ ก็ต่อเมื่อ a < 0
4. สมบัติการคูณด้วยจำนวนเท่ากันที่ไม่เท่ากับศูนย์
ถ้า a > b และ c > 0 แล้ว ac > bc
ถ้า a > b และ c < 0 แล้ว ac < bc
5. สมบัติการตัดออกสำหรับการบวก ถ้า a + c > b + c แล้ว a > b
6. สมบัติการตัดออกสำหรับการคูณ
ถ้า ac > bc และ c > 0 แล้ว a > b
ถ้า ac > bc และ c < 0 แล้ว a < b
บทนิยาม
a ≤ b หมายถึง a น้อยกว่าหรือเท่ากับ b
a ≥ b หมายถึง a มากกว่าหรือเท่ากับ b
a < b < c หมายถึง a < b และ b < c
a ≤ b ≤ c หมายถึง a ≤ b และ b ≤ c
ช่วงของจำนวนจริงและการแก้อสมการ
กำหนดให้ a, b เป็นจำนวนจริง และ a < b
1. ช่วงเปิด (a, b)
(a, b) = { x | a < x < b }
2. ช่วงปิด [a, b]
[a, b] = { x | a ≤ x ≤ b }
3. ช่วงครึ่งเปิด (a, b]
(a, b] = { x | a < x ≤ b }
4. ช่วงครึ่งเปิด [a, b)
[a, b) = { x | a ≤ x < b }
5. ช่วง (a, ∞)
(a, ∞) = { x | x > a}
6. ช่วง [a, ∞)
[a, ∞) = { x | x ≥ a}
7. ช่วง (-∞, a)
(-∞, a) = { x | x < a}
8. ช่วง (-∞, a]
(-∞, a] = { x | x ≤ a}
• การแก้อสมการ
อสมการ คือ ประโยคสัญลักษณ์ที่กล่าวถึงความสัมพันธ์ของตัวแปร กับจำนวนใดๆ โดยใช้เครื่องหมาย ≠ , ≤ ,≥ , < , > , เป็นตัวระบุความสัมพันธ์ของตัวแปร และจำนวนดังกล่าว
คำตอบของอสมการ คือ ค่าของตัวแปรที่ทำให้อสมการเป็นจริง
เซตคำตอบของอสมการ คือ เซตของค่าตัวแปรทั้งหมดที่ทำให้อสมการเป็นจริง
หลักในการแก้อสมการเชิงเส้นตัวแปรเดียว
เราอาศัยสมบัติของการไม่เท่ากันในการแก้อสมการ เช่น
1. สมบัติการบวกด้วยจำนวนที่เท่ากัน
ถ้า a > b แล้ว a + c > b + c
2. สมบัติการคูณด้วยจำนวนที่เท่ากัน
ถ้า a > b และ c > 0 แล้ว ac > bc
ถ้า a > b และ c < 0 แล้ว ac < bc
ตัวอย่างที่ 1 จงหาเซตคำตอบของ x + 3 > 12
วิธีทำ x + 3 > 12
∴ x + 3 + (-3) > 12 + (-3)
x > 9
∴ เซตคำตอบของอสมการนี้คือ (9, ∞)
ตัวอย่างที่ 2 จงหาเซตคำตอบของ 2x + 1 < 9
วิธีทำ 2x + 1 < 9
∴ 2x + 1 + (-1) < 9 + (-1)
2x < 8
(2x) < (8)
x < 4
∴ เซตคำตอบของอสมการนี้คือ (-∞, 4)
ตัวอย่างที่ 3 จงหาเซตคำตอบของ 4x – 5 ≤ 2x + 5
วิธีทำ 4x – 5 ≤ 2x + 5
4x – 5 + 5 ≤ 2x + 5 + 5
4x ≤ 2x + 10
4x – 2x ≤ 2x + 10 – 2x
2x ≤ 10
(2x) ≤(10)
x ≤ 5
∴ เซตคำตอบของอสมการนี้คือ (-∞, 5]
หลักในการแก้อสมการตัวแปรเดียวกำลังสอง
กำหนดให้ a และ b เป็นจำนวนจริงใดๆ
1. ถ้า ab = 0 แล้ว จะได้ a = 0 หรือ b = 0
2. ถ้า = 0 แล้ว จะได้ a = 0
3. ถ้า ab > 0 แล้ว จะได้ a > 0 และ b > 0 หรือ a < 0 และ b < 0
4. ถ้า ab < 0 แล้ว จะได้ a > 0 และ b < 0 หรือ a < 0 และ b > 0
5. ถ้า ab ≥ 0 แล้ว จะได้ ab > 0 หรือ ab = 0
6. ถ้า ab ≤ 0 แล้ว จะได้ ab < 0 หรือ ab = 0
7. ถ้า > 0 แล้ว จะได้ a > 0 และ b > 0 หรือ a < 0 และ b < 0
8. ถ้า < 0 แล้ว จะได้ a > 0 และ b < 0 หรือ a < 0 และ b > 0
9. ถ้า ≥ 0 แล้ว จะได้ > 0 หรือ = 0
10. ถ้า ≤ 0 แล้ว จะได้ < 0 หรือ = 0
ตัวอย่างที่ 4 จงหาเซตคำตอบของ (x – 3)(x – 4) > 0
วิธีทำ ถ้า (x – 3)(x – 4) > 0 แล้วจะได้
x – 3 > 0 และ x – 4 > 0
x > 3 และ x > 4
∴ เมื่อ x – 3 > 0 และ x – 4 < 0 แล้วจะได้ x > 4
หรือ x – 3 < 0 และ x – 4 < 0
x < 3 และ x < 4
∴ x – 3 < 0 และ x – 4 < 0 แล้วจะได้ x < 3
นั่นคือ เซตคำตอบของ (x – 3)(x – 4) > 0 คือ
{ x | x < 3 หรือ x > 4 } = (-∞, 3 ) ∪ (4, ∞ )
ตัวอย่างที่ 5 จงหาเซตคำตอบของ (x – 3)(x – 4) < 0
วิธีทำ ถ้า (x – 3)(x – 4) < 0 แล้วจะได้
x – 3 > 0 และ x – 4 < 0
x > 3 และ x < 4
∴ เมื่อ x – 3 > 0 และ x – 4 < 0 แล้วจะได้ 3 < x < 4
หรือ x – 3 < 0 และ x – 4 > 0
x < 3 และ x > 4 ซึ่งเป็นไปไม่ได้
∴ ไม่มีจำนวนจริง x ที่สอดคล้องกับ x – 3 < 0 และ x – 4 > 0
นั่นคือ เซตคำตอบของ (x – 3)(x – 4) < 0 คือ
{ x | 3 < x < 4 } = (3, 4)
จากตัวอย่างที่ได้กล่าวมาแล้วข้างต้น สรุปเป็นหลักในการแก้อสมกาีได้ดังนี้
กำหนดให้ x, a, b เป็นจำนวนจริง และ a < b แล้ว
1. ถ้า (x – a)(x – b) > 0 จะได้ x < a หรือ x > b
2. ถ้า (x – a)(x – b) < 0 จะได้ a < x < b
3. ถ้า (x – a)(x – b) ≥ 0 จะได้ x ≤ a หรือ x ≥ b
4. ถ้า (x – a)(x – b) ≤ 0 จะได้ a ≤ x ≤ b
5. ถ้า > 0 จะได้ x < a หรือ x > b
6. ถ้า < 0 จะได้ a < x < b
7. ถ้า ≥ 0 จะได้ x ≤ a หรือ x > b
8. ถ้า ≤ 0 จะได้ a ≤ x < b
หรือ สามารถสรุปได้ดังตารางต่อไปนี้
ค่าสัมบูรณ์
บทนิยาม กำหนดให้ a เป็นจำนวนจริง
นั่นคือ ค่าสัมบูรณ์ของจำนวนจริงใดๆ ต้องมีค่ามากกว่าหรือเท่ากับศูนย์เสมอ
• สมบัติของค่าสัมบูรณ์
1. |x| = |-x|
2. |xy| = |x||y|
3. | x – y | = | y – x |
4. |x|2 = x2
5. | x + y | ≤ |x| +|y|
6. เมื่อ a เป็นจำนวนจริงบวก
|x| < a หมายถึง -a < x < a
|x| ≤ a หมายถึง -a ≤ x ≤ a
8. เมื่อ a เป็นจำนวนจริงบวก
|x| > a หมายถึง x < -a หรือ x > a
|x| ≥ a หมายถึง x ≤ -a หรือ x ≥ a