รากที่สองของจำนวนเชิงซ้อน
a =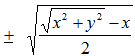 
และ b =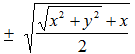 
เเต่บางครั้งค่า y นั้นสามารถเเบ่งได้ออกเป็น 2 กรณีนั่นคือ กรณีที่ค่าของ y มากกว่าหรือเท่ากับ 0 หรือค่าของ y น้อยกว่า 0 เราจึงได้ทฤษฏีบทว่า
กำหนดจำนวนเชิงซ้อน z = x+ yi และให้
r = 
จะได้ว่ารากที่สองของ z คือ
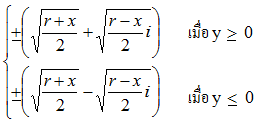
ตัวอย่างที่ 1 จงหารากที่สองของจำนวนเชิงซ้อน −7−24i
ใช้ทฤษฎีหาเลยคับไม่ยากคับ
จากจำนวนเชิงซ้อนที่โจทย์ให้มาคือ −7−24i เมื่อนำไปเทียบกับ x+yi จะเห็นว่า
x=−7 และ y=−24 จะเห็นว่า ค่า y<0 ดังนั้น สูตรที่ใช้ในการหารากที่สองสูตรที่สอง คือ
±(r+x2−−−√−r−x2−−−√i)
เราต้องหา ค่า r ก่อนคับซึ่ง r=√x2+y2
r=√(−7)2+(−24)2
r=√49+576
r=√625
r=25
แทนค่าลงไปในสูตรได้เลยคับจะได้
±(r+x2−−−√−r−x2−−−√i)
±(25+(−7)2−−−−−−√−25−(−7)2−−−−−−√i)
±(182−−√−322−−√i)
±(9√−16−−√i)
±(3−4i)
จะได้ว่า รากที่สองของ −7−24i คือ
3-4i และ -3+4i ไม่ยากแต่ก็ไม่ง่าย ต้องหัดทำน่ะคับเวลาสอบจะได้ทำได้
ตัวอย่างที่ 2 จงหารากที่สองของ -16i
จากจำนวนเชิงซ้อนที่กำหนดให้ คือ -16i =0-16i ถ้าเทียบกับ x+yi จะเห็นว่า x=0 และ y=-16 ซึ่งค่า y<0 ดังนั้นสูตรที่เราใช้ในการหารากที่สองคือ
±(r+x2−−−√−r−x2−−−√i)
เราต้องหาค่า r ก่อนคับ r=√(x2+y2)−−−−−−√ แทนค่าลงไปเลยคับ
r=√02+(−16)2
r=16
แทนค่าลงไปในสูตรอีกคับ
±(16+02−−−−√−16−02−−−−√i)
±(162−−√−162−−√i)
±(8√−8√i)
±(22√−22√i)
จะได้ว่ารากที่สองของ -16i คือ
22√−2i และ −2√+2√i
