รูปแบบของฟังก์ชัน
ชนิดของฟังก์ชัน – คณิตศาสตร์ ม.41. ฟังก์ชันจาก A ไป B
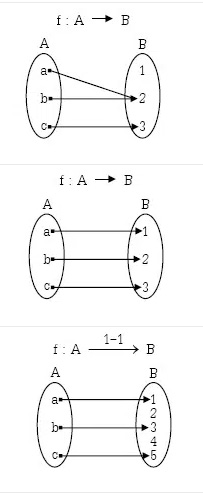
f เป็นฟังก์ชันจาก A ไป B เขียนแทนด้วย f:A→B
หมายความว่า ทุกสมาชิกใน A ต้องมีคู่กับสมาชิกใน B
2.ฟังก์ชันจาก A ไปทั่วถึง B
f เป็นฟังก์ชันจาก A ไปทั่วถึง B เขียนแทนด้วย f:A onto→ B
หมายความว่า ทุกสมาชิกใน A และ B ต้องมีคู่
3.ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B
f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B เขียนแทนด้วย f:A 1-1→ B
หมายความว่า ทุกสมาชิกใน A ต้องมีคู่กับสมาชิกใน B และคู่ไม่ซ้ำ
| • ฟังก์ชันจาก A ไป B | ||
| f เป็นฟังก์ชันจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนคือเซต A และเรนจ์เป็นสับเซตของเซต B เขียนแทนด้วย f : A → B | ||
| • ฟังก์ชันจาก A ไปทั่วถึง B | ||
| f เป็นฟังก์ชันจาก A ไปทั่วถึง B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มีโดเมนเป็นเซต A และเรนจ์เป็นของเซต B เขียนแทนด้วย f : A B | ||
| • ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B | ||
| f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันจาก A ไป B ซึ่งถ้า y ∈ R f แล้วมี x ∈ Df เพียงตัวเดียวเท่านั้นที่ทำให้ (x,y) ∈ f เขียนแทนด้วย f : B หรืออาจกล่าวอย่างง่ายๆได้ว่า f เป็นฟังก์ชันหนึ่งต่อหนึ่ง ก็ต่อเมื่อสำหรับ x1และ x2 ในโดเมน ถ้า f( x1) = f( x2) แล้ว x1 = x2 |
||
| • ฟังก์ชันเพิ่ม ฟังก์ชันลด | ||
| ให้ f เป็นฟังก์ชันจากสับเซตของ R× R และ A ⊂ Df | ||
| ♦ f เป็นฟังก์ชันเพิ่มใน A ก็ต่อเมื่อ สำหรับสมาชิก x1 และ x2 ใดๆ ใน A | ||
|
||
| ♦ f เป็นฟังก์ชันลดใน A ก็ต่อเมื่อ สำหรับสมาชิก x1 และ x2 ใดๆ ใน A | ||
|
||






