ลำดับเลขคณิต (arithmetic sequence)-เลข ม.5

ลำดับเลขคณิต (arithmetic sequence) คือลำดับของจำนวนซึ่งมีผลต่างของสมาชิกสองตัวที่อยู่ติดกันในลำดับเป็นค่าคงตัว ตัวอย่างเช่น ลำดับ 3, 5, 7, 9, 11, 13, … เป็นการก้าวหน้าเลขคณิตที่มีผลต่างร่วมเท่ากับ 2
ถ้าหากพจน์เริ่มต้นของการก้าวหน้าเลขคณิตลำดับหนึ่งคือ a1 และมีผลต่างร่วมของสมาชิกที่อยู่ติดกันเท่ากับ d ดังนั้นพจน์ที่ n ของลำดับนี้คือ  a_n = a₁ + (n−1)d
หรือในกรณีทั่วไป จะได้   a_n = a_m + d(n−m)d
หรือเขียนได้ด้วยรูปแบบความสัมพันธ์เวียนเกิด  a_n = a_n-1 + d

กำหนดให้ a1,a2,a3,...,ana1,a2,a3,…,an เป็นลำดับเลขคณิต

ดังนั้น a1+a2+a3+...+ana1+a2+a3+…+ a_n เป็นอนุกรมเลขคณิต

ให้  sun กันคับว่าหมายความว่าอย่างไร  สมมติว่าผมมีอนุกรมเลขคณิต

2+4+6+8+10+12+...2+4+6+8+10+12+…   ต้องการหา S1,S2,S3,S4S1,S2,S3,S4  

คือผลบวกของหนึ่งพจน์แรก ซึ่งมีค่าเท่ากับพจน์แรกของอนุกรมนั่นเอง

S2=2+4=6S2=2+4=6  ซึ่งก็คือผลบวกสองพจน์แรกของอนุกรม

S3=2+4+6=12S3=2+4+6=12 ซึ่งก็คือผลบวกสามพจน์แรกของอนุกรม

S4=2+4+6+8=20S4=2+4+6+8=20 ซึ่งก็คือผลบวกสี่พจน์แรกของอนุกรม

แต่ถ้าเราต้องการหาสูตรทั่วไปในการในการหาผลบวก n พจน์แรก หรือว่าหา  s_n ซึ่งเจ้าตัวนี้เป็นตัวที่สำคัญมากเราจำเป็นต้องทำความเข้าใจและจำให้ได้ เพราะว่าเป็นเครื่องมือที่สำคัญในการเรียนเรื่องนี้ให้เข้าใจ  สำหรับผลบวก n พจน์แรกของอนุกรมเลขคณิตหรือว่า  s_n นั้นสามารถหาได้จากสูตร

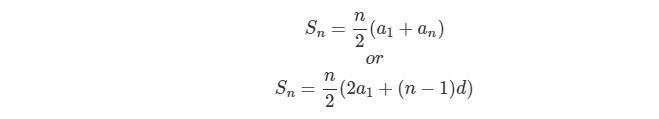
สำหรับสูตรพวกนี้นั้นมันมาได้อย่างไร ก็ต้องอาศัยการพิสูจน์ซึ่งถ้าใครสนใจการพิสูจน์ก็สามารถหาอ่านได้ตามหนังสือ คณิตศาสตร์ของ สสวท. ซึ่งเขาเขียนพิสูจน์ไว้ดีมาก….

สำหรับการทำแบบฝึกหัดเกี่ยวกับเรื่องอนุกรมเลขคณิตนี้ผมก็ได้  สอนและอัดลงวิดีโอข้างล่างนี้แล้วใครสนใจก็ คลิกฟังได้ ไม่เข้าใจตรงไหนก็ถาม ที่สำคัญต้องทำแบบฝึกเพิ่มเติมด้วยน่ะคับ

Example: เขียนกฎและคำนวณเทอมที่ 9 สำหรับลำดับเลขคณิตนี้:

This sequence has a difference of 5 between each number.

ค่าของ a และ d คือ:

• a = 3 (เทอมแรก)
• d = 5 (ค่าความแตกต่างทั่วไป)

การใช้กฎลำดับเลขคณิต:

x_n = a + d(n−1)

= 3 + 5(n−1)

= 3 + 5n − 5

= 5n − 2

So the 9th term is:

x₉ = 5×9 − 2
= 43

1.จงหาผลบวก 50 พจน์แรกของลำดับเลขคณิต 5,7,9,11,13,…

นั่นก็คือหาผลบวก 50 พจน์แรกของอนุกรมเลขคณิต 5+7+9+11+13+…

จาก Sn=n2[2a1+(n−1)d]Sn=n2[2a1+(n−1)d] จะได้

S50=502[2(5)+(50−1)2]S50=502[2(5)+(50−1)2]  จากตรงนี้ d=2 น่ะคับ d=7-5=2

S50=25[10+98]S50=25[10+98]

S50=2700S50=2700

ดังนั้นผลบวก 50 พจน์แรกของอนุกรมนี้คือ 2700

---

2.จงหาผลบวกของอนุกรมเลขคณิต 6+9+12+15+…+99

ข้อนี้ก็คล้ายกับข้อหนึ่งคับ แต่ผมแน่ะนำให้ใช็สูตรนี้ในการหาคำตอบดีกว่า

จากสูตร Sn=n2[a1+an]Sn=n2[a1+an]

การที่เราจะหาผลบวกอนุกรมนี้ได้เราต้องรู้ก่อนว่าอนุกรมเลขคณิตนี้มีทั้งหมดกี่พจน์วิธีการหาคือใช้ความรู้เกี่ยวกับลำดับเลขคณิต คือ

an=a1+(n−1)dan=a1+(n−1)d

99=6+(n−1)399=6+(n−1)3

99=6+3n−399=6+3n−3

3n=99−6+33n=99−6+3

n=963n=963

n=32n=32

จะเห็นว่า อนุกรมนี้มีทั้งหมด 32 พจน์นั้นคือถ้าจะหาผลบวกคือต้องหา S32S32

S32=322[6+99]S32=322[6+99]

s32=1680s32=1680

---

3.ชายคนหนึ่งเริ่มทำงานตั้งแต่ปี พ.ศ.2540 โดยได้รับเงินเดือน 9500 บาท ถ้าเขาได้เงินเดือนขึ้นปีละ 700 บาท จงหาว่าในปี พ.ศ. 2550 เขาจะได้รับเงินเดือนเดือนละเท่าไร

ปี2540 ได้เงินเดือนๆละ  9500  บาท

ปี 2541 ได้เงินเดือนๆละ 9500+700=10200 บาท

ปี 2542 ได้เงินเดือนๆละ 10200+700=10900 บาท

โจทย์ถามว่าในปี 2550 จะได้รับเงินเดือนๆละเท่าไร

ลำดับเลขคณิตภาษาอังกฤษ ใช้คำว่า Arithmetic  Sequence ลำดับเลขคณิตมีลักษณะเป็นเช่นไรนั้น ให้

ลองพิจารณาลำดับที่ผมกำหนดให้ดูดังนี้

1) พิจาารณาลำดับ

1,3,5,7,9,…

จะเห็นว่า ถ้าเอา

3-1=2

5-3=2

7-5=2

9-7=2

นำพจน์ที่อยู่ข้างหลัง ลบ พจน์ที่อยู่ด้านหน้า จะได้ค่าค่าหนึ่งซึ่งคงที่ตลอดจากตัวอย่างคือ 2

ลำดับที่มีลักษณะเช่นนี้ เรียกว่าลำดับ เลขคณิต(Arithmetic Sequence)

---

2) พิจารณาลำดับ

4,8,12,16,20,24,….

จะเห็นว่า ถ้าเอา

8-4=4

12-8=4

16-12=4

20-16=4

24-20=4

นำพจน์ที่อยู่ข้างหลัง ลบ พจน์ที่อยู่ด้านหน้า จะได้ค่าค่าหนึ่งซึ่งคงที่ตลอดจากตัวอย่างคือ 4

ลำดับที่มีลักษณะเช่นนี้ เรียกว่าลำดับ เลขคณิต(Arithmetic Sequence)

จากตัวอย่างข้อ 1) และ 2)

ค่าที่เกิดจากการนำ พจน์ที่อยู่ด้านหลัง ลบ พจน์ที่อยู่ด้านหน้า  ค่าๆนี้เรียนกว่า ผลต่างร่วม(common difference) เราจะแทนผลต่างร่วมด้วยตัว d

ลำดับ 1,3,5,7,9,…

มีผลต่างร่วมหรือว่า d=2

และ

ลำดับ 4,8,12,16,20,24,….

มีผลต่างร่วมหรือ d=4

พจน์ทั่วไปของลำดับเลขคณิตคือ

an=a1+(n−1)d

1.จงหาพจน์ที่ 40 ของลำดับเลขคณิต 1,5,9,13,…

วิธีทำ ข้อนี้เขาให้หา a40a40         นั่นเองครับไม่มีอะไรยุ่งยากคับ

จาก an=a1+(n−1)dan=a1+(n−1)d       ข้อนี้ n=40        a1=1,d=5−1=4a1=1,d=5−1=4

แทนค่าลงไปเลยจะได้

a40=1+(40−1)4a40=1+(40−1)4

a40=1+39(4)a40=1+39(4)

a40=1+156a40=1+156

a40=157a40=157

นั่นคือ พจน์ที่ 40 คือ 157

2.จงหาพจน์ทั่วไปของลำดับเลขคณิต 6,2,-2,-6,…

วิธีทำ เนื่องจากมันลำดับเลขคณิต ดังนั้น จะมีพจน์ทั่วไปคือ

an=a1+(n−1)dan=a1+(n−1)d

จากโจทย์  a1=6,d=2−6=−4a1=6,d=2−6=−4            แทนค่าลงไปเลยคับจะได้

an=6+(n−1)(−4)an=6+(n−1)(−4)

an=6−4n+4an=6−4n+4

an=10−4nan=10−4n            แค่นี้คับเสร็จแล้ว

---

3.จงหาพจน์แรกของลำดับเลขคณิตที่มี     a4=26a4=26           และ     a9=61a9=61

วิธีทำ ข้อนี้จริงๆแล้วคิดในใจได้ แต่ถ้าถามถึงวิธีคิดทั่วไปคือ คิดแบบนี้น่ะ

จากที่เรารู้ คือ an=a1+(n−1)dan=a1+(n−1)d

a4=26a4=26                แทนค่าลงไปเลยจะได้ว่า

<span id=”MathJax-Element-19-Frame” class=”MathJax” style=”font-style: normal;font-weight: normal;line-height: normal;font-size: 16px;text-indent: 0px;text-align: left;text-transform: none;letter-spacing: normal;float: none;direction: ltr;max-width: none;max-height: none;min-width: 0px;min-height: 0px;border: 0px;padding: 0px;margin: 0px” role=”presentation” data-mathml=”26=a1+3d”>26=a1+3d26=a1+3d             ให้เป็นสมการที่ 1

a9=a1+(n−1)da9=a1+(n−1)d          แต่         a9=61a9=61                แทนค่าลงไปเลยจะได้ว่า

61=a1+8d61=a1+8d                   ให้เป็นสมการที่ 2

ข้อนี้เขาให้หา a1a1               จากสมการที่ 1 และ 2  เราสามารถแก้ระบบสมการนี้เพื่อหาค่า  a1a1              ได้น่ะน่าจะมองออก

นำสมการที่ 2 ลบ  สมการที่ 1 จะได้

61−26=(a1+8d)−(a1+3d)61−26=(a1+8d)−(a1+3d)

35=5d35=5d

d=355d=355

d=7d=7

นำค่า d=7 ที่เราได้นี้ไปแทนค่าในสมการที่ 1 หรือ สมการที่ 2 ก็ได้เพื่อหาค่า    a1    ออกมาผมแทนค่าในสมการที่ 1 นะจะได้

26=a1+3d26=a1+3d

26=a1+3(7)26=a1+3(7)

a1=26−21a1=26−21

a1=5a1=5

a1=5a1=5