ลำดับและอนุกรม (Sequences and series)คณิตศาสตร์ ม.ปลาย

ให้ a₁,a₂,a₃ , . . . เป็นลำดับเลขคณิต ผลต่างระหว่างพจน์ที่ n + 1 กับพจน์ที่ n ค่า d (d =a₂ – a₂) ดังนั้น

1) พิจาารณาลำดับ

1,3,5,7,9,…

จะเห็นว่า ถ้าเอา

3-1=2

5-3=2

7-5=2

9-7=2

นำพจน์ที่อยู่ข้างหลัง ลบ พจน์ที่อยู่ด้านหน้า จะได้ค่าค่าหนึ่งซึ่งคงที่ตลอดจากตัวอย่างคือ 2

ลำดับที่มีลักษณะเช่นนี้ เรียกว่าลำดับ เลขคณิต(Arithmetic Sequence)

2) พิจารณาลำดับ

4,8,12,16,20,24,….

จะเห็นว่า ถ้าเอา

8-4=4

12-8=4

16-12=4

20-16=4

24-20=4

นำพจน์ที่อยู่ข้างหลัง ลบ พจน์ที่อยู่ด้านหน้า จะได้ค่าค่าหนึ่งซึ่งคงที่ตลอดจากตัวอย่างคือ 4

ลำดับที่มีลักษณะเช่นนี้ เรียกว่าลำดับ เลขคณิต(Arithmetic Sequence)

จากตัวอย่างข้อ 1) และ 2)

ค่าที่เกิดจากการนำ พจน์ที่อยู่ด้านหลัง ลบ พจน์ที่อยู่ด้านหน้า  ค่าๆนี้เรียนกว่า ผลต่างร่วม(common difference) เราจะแทนผลต่างร่วมด้วยตัว d

ดังนั้นจึงได้ว่า

ลำดับ 1,3,5,7,9,…

มีผลต่างร่วมหรือว่า d=2

และ

ลำดับ 4,8,12,16,20,24,….

มีผลต่างร่วมหรือ d=4

2.ลำดับเรขาคณิต

 ลำดับเรขาคณิต ลำดับที่มีอัตราส่วนของพจน์ที่ n+1 ต่อพจน์ที่ n เป็นค่าคงที่ทุกค่าของจำนวนนับ n และเรียกค่าคงที่นี้ว่า“อัตราส่วนร่วม”เขียนแทนด้วย

ถ้า a₁, a₂, a₃, …, a_n, aⁿ⁺¹ เป็นลำดับเรขาคณิต แล้ว จะได้

การพิจารณาลิมิตของลำดับ

1. ถ้า n → ∞   แล้วทำให้ a_n เข้าใกล้หรือเท่ากับจำนวนจริง L เพียงจำนวนเดียวจะเรียกลำดับ นั้นว่า ลำดับคอน เวอร์เจนต์ (convergent sequence) และมีลิมิตเท่า กับค่า L หรือเรียกว่า ลำดับนั้นลู่เข้าสู่ค่า L

2. ถ้า n → ∞   แล้ว a_n ไม่เข้าใกล้หรือไม่เท่ากับจำนวนจริงใดๆจะ เรียกลำดับนั้นว่า ลำดับ ไดเวอร์เจนต์ (divergent sequence) และเป็นลำดับ ที่ไม่มีลิมิต หรือเรียกว่า ลำดับนั้นลู่ออก

ลำดับคอนเวอร์เจนต์ (Convergent Sequence)

ข้อสังเกตในการพิจารณาการลู่เข้าของลำดับ จะพิจารณาจากกราฟ ดังนี้

1. ลำดับอนันต์ที่มีค่า a_n = L เช่น

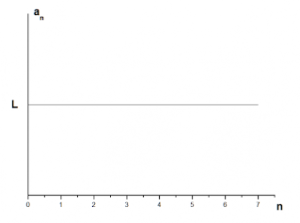
2. ลำดับอนันต์ที่จุด n → ∞ แล้ว a_n = L โค้งเข้าสู่เส้นตรงค่าหนึ่ง

2.1 n → ∞ แล้วทำให้ a_n มีค่าน้อยลง

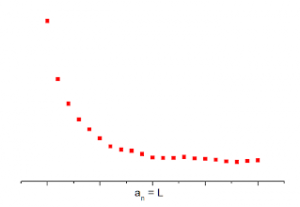
2.2 n → ∞ แล้วทำให้ a_n มีค่ามากขึ้น

3. ลำดับอนันต์ที่จุด n → ∞ แล้ว a_n = L   มีค่าแกว่งไปมาแต่ลู่เข้าสู่เส้นตรงค่าหนึ่ง

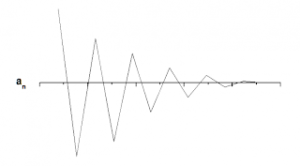
ลำดับไดเวอร์เจนต์ (Divergent Sequence)

ลำดับไดเวอร์เจนต์ เป็นลำดับที่ไม่มีมิลิต ฉะนั้น ลักษณะของกราฟจะไม่วิ่งเข้าหาเส้นตรงที่เป็นจำนวนจริงใดๆ ได้แก่

1.ลำดับ อนันต์ที่จุด n→ ∞ แล้ว  a_n พุ่งขึ้นหรือพุ่งลงอย่างไม่มีขอบเขต

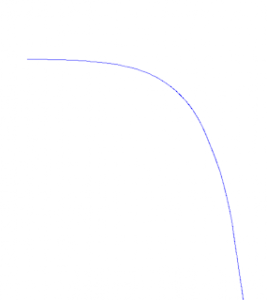
2.ลำดับอนันต์ที่จุด n → ∞ แล้ว a_n มีค่าแกว่งไปมาระหว่างจำนวนจริงมากกว่า 1 ค่า

ตัวอย่างที่ 1 จงพิจารณา ว่า ลำดับ a_n = (-1)³ⁿ เป็นลำดับ ที่มีลิมิตหรือไม่

วิธีทำ หาลำดับนี้ออกมาก่อน นั่นคือ –1, -1, -1, -1, …เขียนกราฟออกมา จะได้กราฟที่มีลักษณะ ดังนี้

เราจะเห็นว่า เมื่อ n มีค่ามากขึ้น พจน์ที่ n ยังมีค่าเท่าเดิม ฉะนั้น ลำดับนี้ เป็นลำดับคอนเวอร์เจนต์ที่ลู่เข้าสู่ –1

ตัวอย่างที่ 2 ลำดับ a_n = 3^n-2 เป็นลำดับคอนเวอร์เจนต์หรือไดเวอร์เจนต์

วิธีทำ  ลำดับ นี้ คือ 1, 4, 7, 10, 13, 16, 19, 22, …

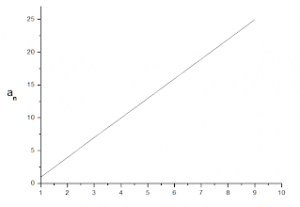
จากกราฟเราจะเห็นว่า พจน์ที่ n จะมีค่าที่พุ่งขึ้นอย่างไม่มีขอบเขต ฉะนั้น ลำดับนี้เป็นลำดับที่ไม่มีลิมิต หรือ ลำดับไดเวอร์เจนต์