วิวัฒนาการของจำนวนและตัวเลข

การผลิตหรือสร้างเครื่องคำนวณได้แนวความคิดมาจาก

1.การจดและนับตัวเลขแบบง่ายๆ ไม่มีการใช้ตัวเลข ชาวกรีกใช้การนับนิ้ว หรือลูกหินแทน

2.การใช้รูปภาพแทนตัวเลขในสมัยอิยิปต์ (egypt) เช่น

ǀ = 1

∩ = 10

3.ชาวบาบิโลเนีย ใช้ลิ่มเป็นสัญลักษณ์ของตัวเลข โดยระบบของจำนวนเลขมีสัญลักษณ์ 2 ตัว

คือ v = 1 = 10

4.สมัยโรมันเริ่มมีการใช้เลขโรมัน ปัจจุบันก็ยังมีใช้อยู่ เช่น

เลขโรมัน

ตัวเลขโรมัน คือ (Roman numerals) เป็นระบบตัวเลขที่ใช้สืบต่อกันมาตั้งแต่ยุคสมัยโรมโบราณ ซึ่งมีการนิยมใช้กันอย่างแพร่หลายในทวีปยุโรป ก่อนที่จะมีตัวเลขฮินดูอารบิกเข้ามาแทนที่อย่างที่ใช้กันอยู่ในปัจจุบัน ซึ่งตัวเลขโรมันจะประกอบไปด้วยสัญลักษณ์พื้นฐานทั้งหมด 7 ตัวหลักด้วยกัน นั่นก็คือ I, V, X, L, C, D และ M สัญลักษณ์เหล่านี้ได้เริ่มใช้ในระหว่างปี 900-800 ปีก่อนคริสต์ศักราช และถึงแม้ว่าในปัจจุบันคนหันมานิยมใช้ตัวเลขฮินดูอารบิกกันแล้ว แต่ตัวเลขโรมันก็ยังปรากฏอยู่ให้เห็นทั่วไป อาทิเช่น ใช้เป็นตัวเลขบนหน้าปัดนาฬิกา, การลำดับหลังชื่อบุคคลสำคัญ หรือระบุบทต่างๆ

เลขโรมัน 1-100

เลขอารบิก	เลข โรมัน
1	I
2	II
3	III
4	IV
5	V
6	VI
7	VII
8	VIII
9	IX
10	X
11	XI
12	XII
13	XIII
14	XIV
15	XV
16	XVI
17	XVII
18	XVIII
19	XIX
20	XX
21	XXI
22	XXII
23	XXIII
24	XXIV
25	XXV
26	XXVI
27	XXVII
28	XXVIII
29	XXIX
30	XXX
31	XXXI
32	XXXII
33	XXXIII
34	XXXIV
35	XXXV
36	XXXVI
37	XXXVII
38	XXXVIII
39	XXXIX
40	XL
41	XLI
42	XLII
43	XLIII
44	XLIV
45	XLV
46	XLVI
47	XLVI
48	XLVIII
49	XLIX
50	L
51	LI
52	LII
53	LIII
54	LIV
55	LV
56	LVI
57	LVII
58	LVIII
59	LIX
60	LX
61	LXI
62	LXII
63	LXIII
64	LXIV
65	LXV
66	LXVI
67	LXVII
68	LXVIII
69	LXIX
70	LXX
71	LXXI
72	LXXII
73	LXXIII
74	LXXIV
75	LXXV
76	LXXVI
77	LXXVII
78	LXXVIII
79	LXXIX
80	LXXX
81	LXXXI
82	LXXXII
83	LXXXIII
84	LXXXIV
85	LXXXV
86	LXXXVI
87	LXXXVII
88	LXXXVIII
89	LXXXIX
90	XC
91	XCI
92	XCII
93	XCIII
94	XCIV
95	XCV
96	XCVI
97	XCVII
98	XCVIII
99	XCIX
100	C

ขอยกตัวอย่างเพิ่มเติมเลข 1-1,000 สามารถแทนด้วยตัวเลขสัญลักษณ์เลขโรมัน ดังต่อไปนี้

1 = I
5 = V
10 = X
50 = L
100 = C
500 = D
1,000 = M

จะเห็นได้ว่าภาษาโรมันหากเป็นเลขโรมัน 1 – 100 จะประกอบไปด้วย 6 สัญลักษณ์ ได้แก่ I, V, X, L, C และ D แต่ถ้าเป็นตัวเลขอังกฤษ 1 – 1,000 จะแทนด้วย สัญลักษณ์ เลขโรมัน ครบทั้งหมด 7 สัญลักษณ์ ได้แก่ I, V, X, L, C, D และ M ซึ่งตัวเลข 1,000 แปลเลขโรมัน คือ สัญลักษณ์ตัว M นั่นเอง

โครงสร้างของระบบจำนวนจิงคือ

แผนผังโครงสร้างของระบบจำนวนจริง

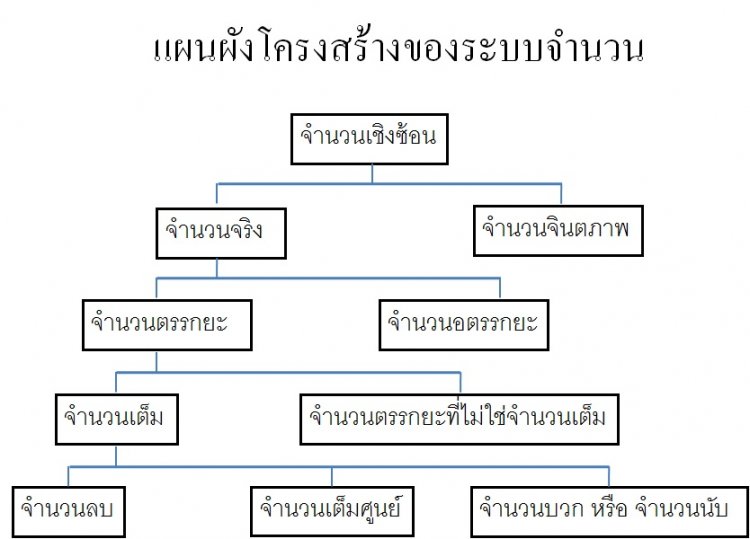
จากรูปแผนผังข้างบนจะเห็นได้ว่า นอกจากจำนวนจริงแล้ว ยังมีจำนวนจินตภาพ ซึ่งเราจะไม่สนใจศึกษาในบทเรียนนี้ นอกจากนี้ เราจะเห็นได้ว่า จำนวนจริงประกอบด้วย จำนวนอตรรกยะ และ จำนวนตรรกยะ ซึ่งเราจะพิจารณาในรายละเอียดได้ดังนี้

จำนวนอตรรกยะ คือ จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือ ทศนิยมซ้ำได้ ยกตัวอย่างเช่น√2, √3,√5 หรือค่า¶ เป็นต้น
จำนวนตรรกยะ คือ จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือ ทศนิยมซ้ำได้ยกตัวอย่างเช่น 1/2, 1/3, 2/5 เป็นต้น

จากแผนภาพอีกเช่นเคย จะเห็นได้ว่า จำนวนตรรกยะ จะประกอบด้วยสองส่วนคือ จำนวนเต็ม และ จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม

จำนวนเต็ม คือจำนวนที่เป็นตัวเลขเต็มๆ หรือ ตัวเลขที่ไม่มีทศนิยมนั่นเอง นั่นคือ ตัวเลขที่เราใช้นับนั่นเอง ยกตัวอย่างเช่น 1, 2, 3, 4 … ทั้งนี้ทั้งนั้น รวมไปจนถึงค่าที่ติบลบของจำนวนนับนี้และศูนย์ด้วย เช่น 0, -1, -2, -3, -4 ….
จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม ความหมายของจำนวนนี้ก็ตามความหมายของชื่อเลยครับ นั่นคือ ตัวเลขเขียนในรูปของทศนิยมซ้ำได้โดยที่ไม่ได้เป็นเลขจำนวนเต็มนั่นเอง อย่างเช่น 1/2=0.5 หรือ 1/3 = 0.333… (สามซ้ำ)

ยิ่งไปกว่านั้น จำนวนเต็มยังแบ่งย่อยได้อีกสามหมวดคือ จำนวนเต็มลบ จำนวนเต็มบวก และ จำนวนเต็มศูนย์

สมบัติของจำนวนจริง

เนื่องจากว่า สมบัติของจำนวนจริงมีเยอะมาก ในที่นี้จะนำเสนอเฉพาะที่คิดว่าสำคัญแล้วกันนะครับ

ถ้าให้ a, b และ c เป็นจำนวนจริงใดๆ แล้ว จะได้ว่าจำนวนจริงจะมีสมบัติดังต่อไปนี้

1. สมบัติปิดการบวก: a+ b จะต้องเป็นจำนวนจริงเสมอ

2. สมบัติการเปลี่ยนหมู่ของการบวก: a + (b + c) = (a + b) + c

3. สมบัติการมีเอกลักษณ์การบวก: a + 0 = a = 0 + a โดยที่เราเรียก 0 ว่าเอกลักษณ์ของการบวก

4. สมบัติการมีอินเวอร์สของการบวก: a + (-a) = 0 = (-a) + a โดยที่ (-a) เป็นอินเวอร์สการบวกของ a

5. สมบัติปิดของการคูณ: a คูณ b หรือ ab จะต้องมีผลลัพธ์เป็นจำนวนจริงเสมอ

6. สมบัติการเปลี่ยนหมู่ของการคูณ: a(bc) = (ab) c

7. สมบัติการมีเอกลักษณ์การคูณ: a x 1 = a = 1 x a โดยที่เราเรียก 1 ว่าเอกลักษณ์ของการคูณ

8. สมบัติการมีอินเวอร์สของการคูณ: a a-1 = 0 = a-1 a โดยที่ a-1 เป็นอินเวอร์สการคูณของ a

9. สมบัติการแจกแจงทางซ้าย: a(b + c) = ab + ac

นอกจากสมบัติของจำนวนจริงแล้ว เรายังมีทฤษฎีบทเบื้องต้นสำหรับจำนวนจริงด้วย ในทำนองเดียวกับสมบัติของจำนวนจริง จะขอนำเสนอเฉพาะส่วนที่คิดว่าสำคัญเท่านั้นนะครับ

ถ้าให้ a, b, c และ d เป็นจำนวนจริงใดๆ จะได้ว่า

1. ถ้า a+c = b+c แล้ว a = b

2. ถ้า c ไม่เท่ากับศูนย์ และ ac =ab แล้ว a = b

3. เมื่อ c > 0 แล้วจะได้ว่า

(1) ถ้า a > b แล้ว ac > bc

(2) ถ้า a < b แล้ว ac < bc

(3) ถ้า ac > bc แล้ว a > b

(4) ถ้า ac < bc แล้ว a < b

4. เมื่อ c < 0 แล้วจะได้ว่า

(1) ถ้า a > b แล้ว ac < bc

(2) ถ้า a < b แล้ว ac > bc

(3) ถ้า ac > bc แล้ว a < b

(4) ถ้า ac < bc แล้ว a > b

5. ถ้า ab = 0 แล้ว a = 0 หรือ b = 0

6. ถ้า a < b และ c < d แล้ว a – d < b – c

3. จำนวนจริง (Real Numbers)

ในขณะนี้มีจำนวนเพียง 2 ประเภทใหญ่ๆ คือ เซตของจำนวนตรรกยะ และเซตของจำนวนอตรรกยะ ผลรวมหรือผลผนวกของเซตทั้งสองนี้เรียกว่า เซตของจำนวนจริง เขียนแทนด้วย R และคุณสมบัติต่างๆ ดังนี้

1. คุณสมบัติปิด (Closure proerties) ถ้า a, b ∊ R

1.1 การบวก a+b ∊ R

1.2 การคูณ a.b ∊ R

2. คุณสมบัติการสลับที่ (Commutative properties) ถ้า a, b ∊ R

2.1 การบวก a+b = b+a

2.2 การคูณ a.b = b.a

3. คุณสมบัติการเปลี่ยนกลุ่ม (Associative properties) ถ้า a, b, c ∊ R

3.1 การบวก a+(b+c) = (a+ b)+c

3.2 การคูณ a. (b .c ) = (a . b) . c

4. คุณสมบัติการแจกแจง (Distributive properties) ถ้า a, b, c ∊ R

4.1 การบวก a+(b . c) = (a+ b) . (a+c)

4.2 การคูณ a. (b + c ) = (a . b) + (a . c)

5. คุณสมบัติการมีเอกลักษณ์ (Identity properties) ถ้า a ∊ R

5.1 เอกลักษณ์ของการบวก คือ 0 เนื่องจาก a + 0 = a

5.2 เอกลักษณ์ของการคูณ คือ 1 เนื่องจาก a . 1 = a

6. คุณสมบัติการมีจำนวนผกผัน (Inverse)

6.1 การบวก ถ้าให้ a ∊ R จะมี -a ∊ R จะทำให้

a + (-a) = (-a) + a = 0 และเรียก -a ว่า เป็นจำนวนผกผัน

6.2 การคูณ ถ้าให้ a ∊ R ที่ a ≠ 0 จะมี 1/a ซึ่งทำให้ a . 1/a = 1/a . a = 1 และเรียก 1/a ว่าเป็นจำนวนผกผันของการคูณของ a

6. จำนวนอตรรกยะ (Irrational Numbers)

จำนวนอตรรกยะ คือ จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปของเศษส่วนได้ เช่น a/b ; b ≠ 0 เมื่อ a, b เป็นจำนวนเต็ม รวมถึงทศนิยมไม่รู้จบแบบไม่ซ้ำ รากที่ถอดได้ไม่ลงตัว หรือเป็นจำนวนที่ไม่ใช่จำนวนตรรกยะ จำนวนอตรรกยะจำแนกได้ดังนี้

1. จำนวนทศนิยมไม่ซ้ำกันไม่รู้จบ

เช่น 1.1707168…

0.4455235…

2. จำนวนที่อยู่ในรูปกรณฑ์ และไม่สามารถหาค่าให้เป็นจำนวนตรรกยะได้

7. จำนวนเต็ม (Integer Numbers)

จำนวนเต็ม คือ จำนวนที่เป็นเลขไม่มีเศษ เช่น -5 , 0 , 3 เป็นต้น

สัญลักษณ์

I แทนจำนวนเต็ม เช่น … , -2 , -1 , 0 , 1 , 2 , …

I^– แทนจำนวนเต็มลบ เช่น -1 , -2 , -3 , -4 , …

I⁺แทนจำนวนเต็มบวก เช่น 1, 2 , 3 , 4 ,…

N แทนจำนวนธรรมชาติ หรือจำนวนนับ เช่น 1, 2 , 3 , 4 ,…

8. จำนวนเต็มบวก และศูนย์ (Whole Numbers)

ให้ w แทนเซตของจำนวนเต็มบวก และศูนย์

ดังนั้น w = { 0, 1, 2, 3, …}

สำหรับคุณสมบัติการบวกและการคูณ จะเป็นเช่นเดียวกับจำนวนนับ แต่มีจำนวนศูนย์ โดยมีคุณสมบัติดังนี้

1. ให้ a ∊ w a + 0 = 0 + a = a

2. ให้ a ∊ w a – 0 = a

3. ให้ a ∊ w 0/a = 0

0/a ไม่สามารถหาคำตอบได้ ซึ่งนั่น ให้นิยามไม่ได้ เพราะโดยธรรมชาติไม่มีการหารจำนวนใดๆด้วยศูนย์ ซึ่งเป็นจำนวน จำนวนหนึ่ง ให้ 0/0 = r จะได้ r .0 = 0 ดังนั้น r จะเป็นจำนวนใดๆ ก็ได้ทั้งนั้นหมายความว่า 0/0 ไม่ค่าไม่แน่นอน ผลหารในกรณีนี้ ไม่เป็นที่ยอมรับในคณิตศาสตร์ จึงไม่มีการหาร 0 ด้วย 0 และ w ก็มีคุณสมบัติเช่นเดียวกับเซตจำนวนนับ

9. จำนวนนับ หรือจำนวนธรรมชาติ หรือจำนวนเต็มบวก (Counting or Natural or Positive Integers)

จำนวนนับ เรียกอีกอย่างว่า จำนวนธรรมชาติ หรือจำนวนเต็มบวก มนุษย์จำนวนนับ หรือจำนวนธรรมชาติไปใช้ในชีวิตประจำวันมากที่สุด ในการแลกเปลี่ยน ซื้อ – ขาย หรือการนับ และมนุษย์จะนับเลขเริ่มจาก 1, 2, 3, 4, 5, … ไปเรื่อยๆ เสมอไม่นิยมนับเลข -1, -2, -3, -4 นอกจาก นำมาใช้ในบางกรณีเท่านั้น ดังนั้น เราจึงละไว้ในฐานที่เข้าใจว่า จำนวนนับ คือ จำนวนธรรมชาติ และจำนวนเต็มบวก

ให้ N แทนเซตของจำนวนนับ สมาชิกของ N คือ 1, 2, 3, 4, …

นั่นคือ N = {1, 2, 3, 4, …}

10. เส้นจำนวน (Number Line)

ลากเส้นตรงเส้นหนึ่ง เกิดจากจุดหลายๆ จุดมาเรียงต่อกันไปตามแนวตั้ง หรือแนวนอนก็ได้ โดยเริ่มจากจุดกำเนิด (Origin) ซึ่งถือว่าเป็นจุดเดียวกับจำนวนจริง 0 ดังนั้น บนเส้นตรงให้มีจุดนี้แทนจำนวนศูนย์จุด บนเส้นตรงขวามือของ 0 เป็นจำนวนเต็มบวกแทนด้วย 1, 2, 3, 4, … โดยมีระยะห่างจาก 0 เป็น 1 หน่วย , 2 หน่วย , 3 หน่วย , … ตามลำดับ และเลือกจุดบนเส้นจำนวนทางซ้ายมือของ 0 เป็นจำนวนเต็มลบแทนด้วย -1, -2 , -3 ,… โดยมีระยะห่างจาก 0 เป็น 1 หน่วย , 2 หน่วย , 3 หน่วย , … ตามลำดับ