สถิติและข้อมูล-การวิเคราะห์ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล คณิตศาสตร์ม.ปลาย

การวิเคราะห์ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล

             ในการวิเคราะห์ข้อมูลบ่อยครั้งมีข้อมูลเชิงปริมาณที่ประกอบด้วยตัวแปรตั้งสองตัวขึ้นไป และตัวแปรเหล่านั้นมีความเกี่ยวข้องกันอยู่ เช่น รายได้และรายจ่ายของครอบครัว ส่วนสูงและน้ำหนักของเด็กแรกเกิด ความเกี่ยวข้องกันของตัวแปรจะมีลักษณะที่ค่าของตัวแปรหนึ่งขึ้นอยู่กับอีกตัวแปรหนึ่ง เช่น รายจ่ายจะขึ้นอยู่กับรายได้ ส่วนสูงจะขึ้นอยู่กับน้ำหนักกรณีเช่นนี้ จะเรียกตัวแปรที่แสดงรายได้หรือน้ำหนักว่าตัวแปรอิสระ (independent variables)เรียกตัวแปรที่แสดงรายจ่ายหรือส่วนสูงว่า ตัวแปรตาม(dependent variables)

ตัวอย่างที่ 1 จงหาความสัมพันธ์ x กับ y

x                             y		xy		x2
1 2 4 6	5 8 14 20		5 16 56 120		1 4 16 36
Σx = 13	Σy = 47		Σxy = 197		Σx2 = 57

 

วิธีทำ

Σy       =   cn+ mΣx…………….1)

Σxy     =   cΣx+ mΣx²…………….2)

47      =   4c + 13m…………….1)

197    =   13c + 57m………………2)

1) x 13         611   =   52c + 169m………………3)

2) x 4           788   =   52c + 228m………………4)

4) –3)           177   =   59m

จะได้       m   =   3

แทน  m = 3 ใน 1)     47   =  4c + 13(3)

                                 47   =  4c + 39

                                   8   =  4c

ฉะนั้น             c   =  2

แทนค่าในสมการ     y = mx+ c

                 จะได้    y  =   3x + 2     ans

โดยทั่วๆไป ความสัมพันธ์เชิงฟังก์ชันของข้อมูลที่ประกอบ ด้วยตัวแปรสองตัวแปรอาจแบ่งออกเป็นสองชนิดใหญ่ๆคือ

     

ความสัมพันธ์ของฟังก์ชันที่กราฟเป็นเส้นตรง

            สมการทั่วไปของความสัมพันธ์เชิงฟังก์ชันเป็น y= a+bx  เมื่อ y เป็นตัวแปรตาม และ x เป็นตัวแปรอิสระ

b เป็นความชันของเส้นตรงหรือค่าของ yที่เปลี่ยนไป  เมื่อ x เปลี่ยนไปหนึ่งหน่วย a เป็นระยะตัดแกน y   และเป็นค่าคงตัวที่ต้องการหา ความสัมพันธ์เชิงฟังก์ชันที่กราฟไม่เป็นเส้นตรง ในที่นี้จะกล่าวเฉพาะความสัมพันธ์ที่มีกราฟเป็นพาราโบลา และรูปเอกซ์โพเนนเชียล  ซึ่งมีรูปสมการของความสัมพันธ์เชิงฟังก์ชัน ดังนี้

y = a+bx+cx² และ y = abx ตามลำดับ เมื่อ y เป็นตัวแปรตาม และ x เป็นตัวแปรอิสระ   a,bและ c เป็นค่าคงตัวที่จะต้องหา

ภาพการกระจาย

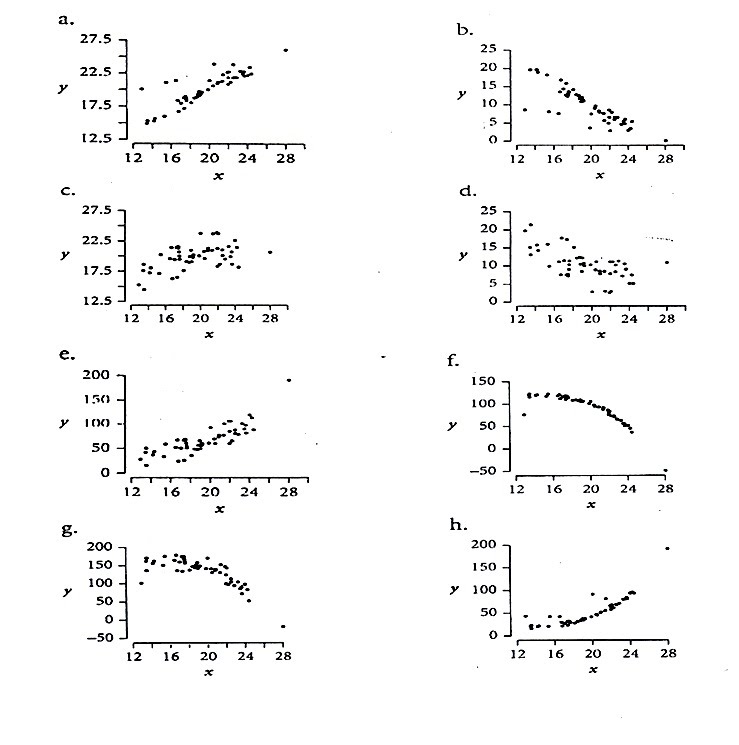
             ในการสร้างความสัมพันธ์เชิงฟังก์ชันของข้อมูลเชิงปริมาณที่ประกอบด้วยตัวแปรสองตัวจากข้อมูลที่มีอยู่ทั้งหมด หรือจากตัวอย่างข้อมูลที่เลือกมาเป็นตัวแทนของข้อมูลที่มีอยู่ มีความจำเป็นที่จะต้องตรวจดูรูปแบบของความสัมพันธ์ที่เกิดขึ้นระหว่างตัวแปรทั้งสอง เพื่อที่จะนำมาใช้ในการกำหนดความสัมพันธ์เชิงฟังก์ชันที่จะสร้างขึ้นรูปแบบของความสัมพันธ์นี้ พิจารณาได้จากกราฟที่สร้างจากข้อมูลที่มีอยู่ทั้งหมดหรือจากข้อมูลนั้นๆ บางครั้งการพิจารณาจากแผนภาพการกระจายไม่สามารถบอกลงไปได้แน่นอน ว่ามีรูปของความสัมพันธ์เป็นแบบใด เนื่องจากลักษณะการกระจายไม่สามารถจัดเข้าในรูปความสัมพันธ์เชิงฟังก์ชันใดๆได้ หรืออาจจะมีลักษณะของความสัมพันธ์ที่ใกล้เคียงกับรูปของความสัมพันธ์เชิงฟังก์ชันที่เป็นเส้นตรง หรือเป็นเอกซ์โพเนนเชียลก็ได้ในกรณีนี้ถ้าผู้สร้างความสัมพันธ์มีความรู้ความชำนาญเกี่ยวกับข้อมูลชนิดนั้นๆ อาจจะบอกได้ว่าควรจะสร้างความสัมพันธ์ไม่ต้องการความละเอียดถูกต้องจากการพยากรณ์ค่าตัวแปรตาม จากความสัมพันธ์ที่สร้างขึ้นนั้นมากนักก็อาจจะเลือกใช้รูปของความสัมพันธ์เชิงฟังก์ชันที่ง่ายต่อการคำนวณ สรุปได้ว่าการกำหนดรูปแบบของความสัมพันธ์ระหว่างตัวแปรเชิงปริมาณทั้งสองโดยพิจารณาจากแผนภาพการกระจาย (ในรูปต่อไป) จะขึ้นอยู่กับความชำนาญเกี่ยวเรื่องที่น้ามาสร้างความสัมพันธ์ของผู้สร้างความสัมพันธ์นั้นและความละเอียดถูกต้องของค่าพยากรณ์ที่ต้องการเป็นสำคัญ

         แผนภาพการกระจาย 8 รูปนี้ แต่ละรูปแสดงแนวโน้ม (trend) ของความสัมพันธ์เชิงฟังก์ชัน ระหว่างตัวแปรอิสระ(x) และตัวแปรตาม(y)ในรูปของกราฟที่มีแนวโน้ม 2 แบบหลักๆ แบบที่ 1 คือ แบบเป็นเส้นตรง ซึ่งสามารถพิจารณาเป็น 2 กรณี คือ กรณีที่มีแนวโน้มเป็นทางบวก (positive trend) หมายความว่า เมื่อค่าของ X เพิ่มขึ้น ค่าของ Y จะเพิ่มขึ้นด้วยและกรณีที่มีแนวโน้มทางลบ (negative trend) หมายความว่า เมื่อค่าของ X เพิ่มขึ้น ค่าของY กลับลดลง ส่วนแนวโน้มของความสัมพันธ์เชิงฟังก็แบบที่ 2 คือ แบบไม่เป็นเส้นตรง ซึ่งก็พิจารณาเป็น 2 กรณี เช่นเดียวกันกับแนวโน้มของความสัมพันธ์ที่มีลักษณะเป็นเส้นตรง คือ อาจมีแนวโน้มทางบวกหรือทางลบได้

การประมาณค่าของค่าคงตัวโดยใช้วิธีกำลังสองน้อยสุด

           เมื่อทราบถึงรูปแบบของความสัมพันธ์เชิงฟังก็ชันของข้อมูลจากการสร้าแผนภาพการกระจายของข้อมูลว่าควรอยู่ในรูป

แบบใด เช่น รูปเส้นตรง รูปพาราโบลา หรือรูปเอกซ์โพเนนเชียลแล้วขั้นต่อไปก็คือการหาสมการของความสัมพันธ์ โดยเริ่มจาก

สมการทั่วไปรูปใดรูปหนึ่งคือ Y = a + bX, Y = a + bX+ cX2 หรือ Y = abXแล้วประมาณค่าของค่าคงตัวในสมการที่เลือก เมื่อทราบค่าคงตัวแล้ว จึงสามารถนำไปใช้ในการพยากรณ์ค่าตัวแปรตามเมื่อทราบหรือกำหนดค่าตัวแปรอิสระได้

     ในการหาค่าคงตัวที่ปรากฏอยู่มนสมการทั่วไปนั้น หาได้โดยอาศัยหลักที่ว่า ถ้าจะให้สมการของความสัมพันธ์ที่สร้างขึ้นสามารถใช้แทนความสัมพันธ์ที่เกิดขึ้นได้ดีแล้ว ผลรวมจองความแตกต่างระหว่างค่าที่ได้จากความสัมพันธ์เชิงฟังก์ชันที่สร้างขึ้นกับค่าที่เกิดขึ้นจริงทุก ๆ ค่าควรจะน้อยที่สุด แต่เนื่องจากความแตกต่างระหว่างค่าที่ได้จากความสัมพันธ์เชิงฟังก์ชันแต่ละค่ากับค่าที่เกิดขึ้นจริงอาจมีค่าเป็นบวกบ้าง ลบบ้าง ขึ้นอยู่กับแต่ละค่าของความสัมพันธ์กับค่าที่เกิดขึ้นจริงว่าค่าใดจะมากกว่ากัน ท้าให้ผลรวมของความแตกต่างดังกล่าวอาจจะหักล้างกันหมดพอดี

            ดังนั้นผลรวมของความแตกต่างที่เกิดขึ้นเป็นศูนย์ซึ่งไม่ตรงกับความจริง เพราะความแตกต่างที่เกิดขึ้นระหว่างค่าจากความสัมพันธ์และค่าที่เกิดขึ้นจริงไม่ว่าจะมากกว่าหรือน้อยกว่าจะเป็นความแตกต่างซึ่งถือว่าเป็นความคลาดเคลื่อนที่เกิดขึ้นหมดไปได้ ดังนั้น เพื่อที่จะไม่ให้ผลรวมของความแตกต่างที่เกิดขึ้นเป็นศูนย์ จึงต้อง…

วิธีที่จะทำให้ มีค่าที่สุดจะไม่แสดงไว้ในที่นี้ เนื่องจากต้องใช้ความรู้คณิตศาสตร์ชั้นสูง แต่จากการใช้วิธีกาลังสองน้อยที่สุดดังกล่าวจะได้สมการซึ่งเรียกว่าสมการปกติ โดยมีจานวนสมการเท่ากับจานวนคงตัว ที่ต้องการหา กล่าวคือ

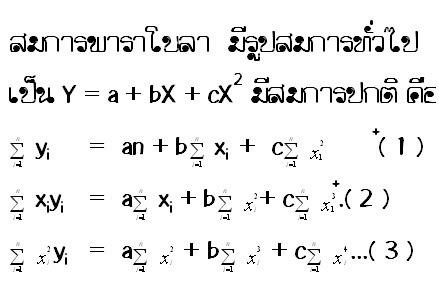
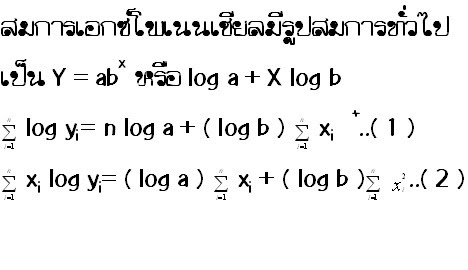
            เมื่อ (x_i,y_i) เป็นค่าจากการสังเกตจากตัวแปรอิสระและตัวแปรอิสระและตัวแปรตามคู่ที่ iเมื่อ iคือ 1,2,3,…,n และ a,b,cเป็นค่าคงตัวค่าคงตัวของสมการของสัมพันธ์เชิงฟังก์ชันแบบต่างๆหาได้จากการแก้สมการปกติหลังจากหลังจากที่ได้แทนค่าคงตัวแปรอิสระและตัวแปรตามที่น้ามาสร้างความสัมพันธ์นั้นแล้ว

 

ความสัมพันธ์เชิงฟังก์ชันของข้อมูลเชิงอนุกรมเวลา

            ข้อมูลที่อยู่ในรูปของอนุกรมเวลา (time series) คือ ข้อมูลที่แสดงความเปลี่ยนแปลงตามลำดับก่อนหลังของช่วงเวลาที่เหตุการณ์นั้น ๆ เกิดขึ้น ซึ่งปกติแล้วข้อมูลนั้น ๆ มักจะเกิดขึ้นในช่วงเวลาเท่า ๆ กัน เช่น ปริมาณข้าวที่ประเทศไทยผลิตได้ในแต่ละปี จ้านวนเงินที่ร้านค้าแห่งหนึ่งขายได้ในแต่ละเดือนหรืออุณหภูมิเฉลี่ยในแต่ละวันในจังหวัดกาญจนบุรี เป็นต้น จากตัวอย่างที่ยกมาแสดงนี้ จะเห็นได้ว่า ปริมาณข้าวที่ประเทศไทยผลิตได้ จำนวนเงินที่ร้านค้าแห่งหนึ่งขายได้ หรืออุณหภูมิเฉลี่ยในแต่ละวันของจังหวัดกาญจนบุรี เป็นข้อมูลที่มีความเกี่ยวข้องกับเวลาทั้งสิ้น นั่นคือ ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูลที่สนใจศึกษา(y)กับช่วงเวลาที่ข้อมูลนั้นเกิด(t) เขียนได้เป็น y=f(t)เมื่อ t เป็นตัวแปรอิสระ และ y เป็นตัวแปรตามความสัมพันธ์เชิงฟังก์ชันของข้อมูลเชิงอนุกรมเวลา

            ในการสร้างความสัมพันธ์เชิงฟังก์ชันของข้อมูลที่อยู่ในรูปอนุกรมเวลานี้ ใช้วิธีเดียวกันกับที่ใช้ในการสร้างความสัมพันธ์เชิงฟังก์ชันของตัวแปรอิสระและตัวแปรตามที่ได้กล่าวมาแล้ว นั่นคือ กำหนดรูปของความสัมพันธ์เชิงฟังก์ชันของข้อมูลที่สนใจศึกษากับช่วงเวลาที่ข้อมูลนั้น ๆ เกิดขึ้น จากแผนภาพการกระจายของข้อมูลที่มีอยู่หรือที่เลือกขึ้นมาเป็นตัวแทนจากข้อมูลที่มีอยู่ทั้งหมด แล้วประมาณค่าของค่าคงตัวจากความสัมพันธ์ที่ได้กำหนดไว้นั้น โดยใช้วิธีกำลังสองน้อยสุดที่ได้กล่าวมาแล้ว

       สำหรับการแทนค่า t ของเวลาที่เท่า ๆ กัน ซึ่งอาจจะเป็นวัน เดือน พุทธศักราช หรือ คริสต์ศักราช นั้น โดย ๆ ไป ถ้าจำนวนช่วงเวลาที่นำมาสร้างความสัมพันธ์เป็นจำนวนคี่มักจะกำหนดช่วงเวลาที่อยู่ตรงกลางเป็น 0 และช่วงเวลาที่อยู่ถัดขึ้นไปก่อนหน้าช่วงเวลาที่กำหนดให้เป็น 0 นี้เป็น –1, -2, -3, … ตามล้าดับ ส่วนช่วงเวลาที่อยู่ถัดลงมา ซึ่งเป็นช่วงเวลาที่เกิดขึ้นภายหลังจะกำหนดเป็น 1, 2, 3, … ตามลำดับ ดังนี้ ในหัวข้อ 3.4 จึงเป็นการศึกษาเชิงฟังก์ชัน โดยเน้นเฉพาะแนวโน้มตามเวลาที่ใช้เป็นตัวแปรอิสระ (t) เพื่อใช้รูปแบบสมการที่ประมาณได้มาพยากรณ์ค่าของตัวแปรตาม (y) ต่อไป

       ในกรณีที่จำนวนช่วงเวลาที่น้ามาสร้างความสัมพันธ์เป็นจำนวนคู่มักจะแทนสองช่วงเวลาที่อยู่ตรงกลางเป็น –1 และ 1 และแทนช่วงเวลาที่อยู่ถัดขึ้นไปก่อนหน้าช่วงเวลาที่กำหนดให้เป็น –3, -5, -7, … ตามลำดับ ส่วนช่วงเวลาที่เกิดขึ้นภายหลังแทนด้วย                3, 5, 7, … ตามลำดับ ในการกำหนดค่าดังกล่าวขึ้นมาใช้แทนตัวแปรซึ่งเป็นช่วงเวลานี้ ก็เพื่อให้การคำนวณหาค่าคงตัวท้าได้สะดวก  และรวดเร็วขึ้น เพราะผลรวมของทุก ๆ ค่าของt จะเท่ากับ 0 และในการพยากรณ์ค่าของตัวแปรตาม จะต้องเปลี่ยนช่วงเวลาให้อยู่ในรูปของค่า t ที่กำหนดให้โดยวิธีดังกล่าวด้วย

ขอขอบคุณ https://kruamm.files.wordpress.com