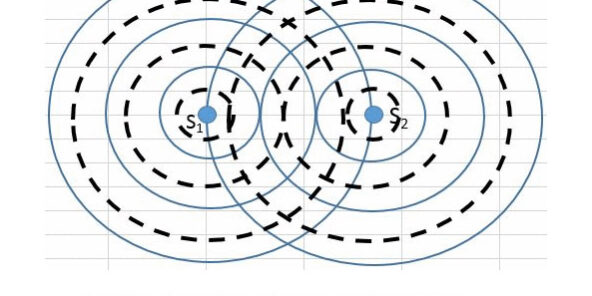
สมการการแทรกสอดของแสง
ถ้าให้ ช่องแคบ S1 และ S2 เป็นแหล่งกำเนิดแสงห่างกันเป็นระยะ d เมื่อแสงเดินทางจากช่องแคบมาถึงฉากด้วยระยะทางที่ต่างกัน เดินทางมาพบกันบนจุดเดียวกัน คือ จุด P จะได้ผลต่าง S1P กับ S2P จากภาพที่ 7 การแทรกสอดของแสง พบว่า
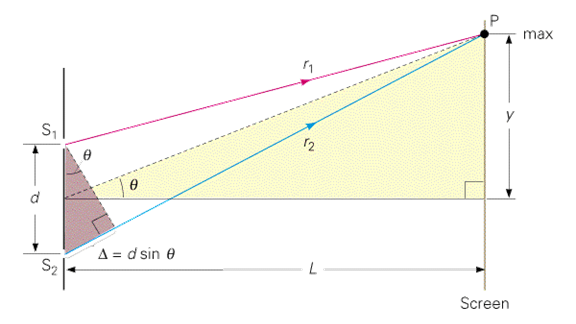
S2P – S1P = dsinθ
เนื่องจากมุมเป็นมุมน้อย ๆ จะได้ tanθ = sinθ สามารถสรุปสมการที่ใช้คำนวณเกี่ยวกับสลิตคู่ ดังนี้
1. เมื่อ S1 , S2 มีเฟสตรงกัน
การแทรกสอดแบบเสริมกัน (แนวกลางเป็นแนวปฏิบัพ A0)
S2P – S1P = nλ
d sinθ = nλ
d y/L = nλ
เมื่อ n = 0, 1, 2, 3, ….
การแทรกสอดแบบหักล้างกัน
S2P – S1P = (n-1/2)λ
d sinθ = (n-1/2)λ
d y/L = (n-1/2)λ
เมื่อ n = 1, 2, 3, ….
2. เมื่อ S1 , S2 มีเฟสตรงข้ามกัน
การแทรกสอดแบบเสริมกัน
S2P – S1P = (n-1/2)λ
d sinθ = (n-1/2)λ
d y/L = (n-1/2)λ
เมื่อ n = 1, 2, 3, ….
การแทรกสอดแบบหักล้างกัน (แนวกลางเป็นแนวบัพ N0)
S2P – S1P = nλ
d sinθ = nλ
d y/L = nλ
เมื่อ n = 0, 1, 2, 3, ….
สรุป และตัวอย่างอย่าง

S1P – S2P = d sinθ
ถ้าให้ ช่องแคบ S1 และ S2 เป็นแหล่งกำเนิดแสงห่างกันเป็นระยะ d เมื่อแสงเดินทางจากช่องแคบมาถึงฉากด้วยระยะทางที่ต่างกัน สามารถสรุปสมการที่ใช้คำนวณเกี่ยวกับสลิตคู่ ดังนี้
1. เมื่อ S1 , S2 มีเฟสตรงกัน
การแทรกสอดแบบเสริมกัน (แนวกลางเป็นแนวปฏิบัพ A0)
S1P – S2P = nλ
d sinθ = nλ
d y/L = nλ
เมื่อ n = 0, 1, 2, 3, ….
การแทรกสอดแบบหักล้างกัน
S2P – S1P = (n-1/2)λ
d sinθ = (n-1/2)λ
d y/L = (n-1/2)λ
เมื่อ n = 1, 2, 3, ….
2. เมื่อ S1 , S2 มีเฟสตรงข้ามกัน
การแทรกสอดแบบเสริมกัน
S2P – S1P = (n-1/2)λ
d sinθ = (n-1/2)λ
d y/L = (n-1/2)λ
เมื่อ n = 1, 2, 3, ….
การแทรกสอดแบบหักล้างกัน (แนวกลางเป็นแนวบัพ N0)
S2P – S1P = nλ
d sinθ = nλ
d y/L = nλ
เมื่อ n = 0, 1, 2, 3, ….
ตัวอย่าง ช่องแคบคู่มีระยะห่างระหว่างช่อง 0.1 มิลลิเมตร เมื่อฉายแสงความยาวคลื่น 600 นาโนเมตร ผ่านช่องแคบคู่ ปรากฎว่าแถบสว่างลำดับที่สองบนฉากห่างออกไป 80 เซนติเมตร จะอยู่ห่างจากแนวกลางเท่าใด
แนวคิด จากปัญหานี้เราทราบว่า d = 0.1 x 10-3 m, λ = 600 x 10-9 m , L = 0.8 m และ n = 2 ต้องการทราบระยะห่างของแถบสว่างที่สองจากตรงกลาง y = ?
จากความสัมพันธ์
d y/L = nλ
(0.1 x 10-3 m) y/(0.8 m) = 2 (600 x 10-9 m)
y = 9.6 x 10-3 m
y = 9.6 mm
ตอบ แถบสว่างลำดับที่สองอยู่ห่างจากแนวกลาง 9.6 มิลลิเมตร