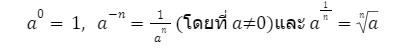ฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึม-สมบัติของเลขยกกำลัง
กำหนดให้ a , b เป็นจำนวนจริงใด ๆ
ลขยกกำลัง
- เลขยกกำลัง คือจำนวนที่เขียนในรูป an โดยเรียก a ว่าฐาน และเรียก n ว่า เลขชี้กำลัง (Exponent) ซึ่งถ้าเลขชี้กำลัง n เป็นจำนวนนับ แล้ว an จะแทน a คูณกันเป็นจำนวน n ตัว หรือ
an=a∙a∙a∙… ∙a (n ตัว)
แต่ถ้าเลขชี้กำลังเป็นศูนย์ หรือจำนวนลบ หรือเศษส่วน จะเป็นไปตามนิยามดังนี้
ข้อ 1 สมบัติการคูณเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก
เมื่่อ a เป็นจำนวนใด ๆ และ m, n เป็นจำนวนเต็มบวก
ตัวอย่างเช่น 23x 27x 29 = 2 (3 + 7 + 9) = 219
ข้อ 2 สมบัติการหารเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก
กรณีที่ 1 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m > n
ตัวอย่างเช่น 412÷ 43=412-3 = 49
ข้อที่ 3 นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ และ n เป็นจำนวนเต็มบวก แล้ว
ข้อที่ 4 ยกกำลังอยู่ด้านนอกคูณเข้าในได้
ข้อที่ 5 ยกกำลังอยู่ด้านนอกคูณเข้าในได้
ข้อที่ 6 ยกกำลังอยู่ด้านนอกคูณเข้าในได้
ข้อที่ 7 จำนวนยกกำลัง ศูนย์ ได้เท่ากับ 1
ข้อที่ 8 1 ยกกำลังอะไรก็ได้ 1