สรุปตรรกศาสตร์เบื้องต้น-คณิตศาสตร์ออนไลน์ ม.4

ตรรกศาสตร์ หมายถึง

ตรรกศาสตร์ เป็นวิชาที่ว่าด้วยกฎเกณฑ์และเหตุผล การได้มาของผลภายใต้กฎเกณฑ์ที่กำหนดถือเป็นสาระสำคัญ ข้อความหรือการให้เหตุผลในชีวิตประจำวันสามารถสร้างเป็นรูปแบบที่ชัดเจนจน ใช้ประโยชน์ในการสรุปความ ความสมเหตุสมผลเป็นที่ยอมรับกันอย่างกว้างขวาง ตรรกศาสตร์เป็นแม่บทของคณิตศาสตร์แขนงต่าง ๆ และการประยุกต์

ประพจน์ (Propositions/Statement)

สิ่งแรกที่ต้องรู้จักในเรื่องตรรกศาสตร์คือ ประพจน์ ข้อความหรือประโยคที่มีค่าความจริง(T)หรือเท็จ(F) อย่างใดอย่างหนึ่ง ส่วนข้อความรูป คำสั่ง คำขอร้อง คำอุทาน คำปฏิเสธ ซึ่งไม่อยู่ในรูปของประโยคบอกเล่า จะเป็นข้อความที่ไม่เป็นประพจน์ สำหรับข้อความบอกเล่าแต่มีตัวแปรอยู่ด้วย ไม่สามารถบอกว่าเป็นจริงหรือเท็จจะไม่เป็นประพจน์ เรียกว่าประโยคเปิด

ประโยคที่มีค่าความจริงไม่แน่นอน หรือไม่อาจระบุได้ว่ามีค่าความจริงเป็นจริงหรือเป็นเท็จได้ ไม่เป็นประพจน์

การเชื่อมประพจน์

โดยปกติเมื่อกล่าวถึงข้อความหรือประโยคนั้นมักจะมีกริยามากกว่าหนึ่งตัว แสดงว่าได้นำประโยคมาเชื่อมกัน มากกว่าหนึ่งประโยค ดังนั้นถ้านำประพจน์มาเชื่อมกัน ก็จะได้ประพจน์ใหม่ ซึ่งสามารถบอกได้ว่าเป็นจริงหรือเป็นเท็จ ตัวเชื่อมประพจน์มีอยู่ 5 ตัว และตัวเชื่อมที่ใช้กันมากในตรรกศาสตร์คือ และ หรือ ถ้า…แล้ว ก็ต่อเมื่อ ไม่

ตัวเชื่อมประพจน์ “และ”
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “และ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∧ q ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงเป็นจริง (T) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นเท็จ (F)
ตัวเชื่อมประพจน์ “หรือ”
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “หรือ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ∨q ซึ่งจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p และ q มีค่าความจริงเป็นเท็จ (F) ทั้งคู่ นอกนั้นมีค่าความจริงเป็นจริง (T)
ตัวเชื่อมประพจน์ “ถ้า…แล้ว”
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “ถ้า…แล้ว” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p → q ซึ่งจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p เป็นจริง (T) และ q เป็นเท็จ (F) นอกนั้นมีค่าความจริงเป็นจริง (T)
ตัวเชื่อมประพจน์ “ก็ต่อเมื่อ”
การเชื่อม p และ q เข้าด้วยกันด้วยตัวเชื่อมประพจน์ “ก็ต่อเมื่อ” สามารถเขียนแทนได้ด้วยสัญลักษณ์ p ⇔ q ซึ่งจะมีค่าความจริงเป็นจริง (T) เมื่อ p และ q มีค่าความจริงตรงกัน และจะมีค่าความจริงเป็นเท็จ (F) เมื่อ p และ q มีค่าความจริงตรงข้ามกัน
นิเสธของประพจน์ “ไม่”
นิเสธของประพจน์ใดๆ คือ ประพจน์ที่มีค่าความจริงตรงกันข้ามกับประพจน์นั้นๆ และสามารถเขียนแทนนิเสธของ p ได้ด้วย ~p

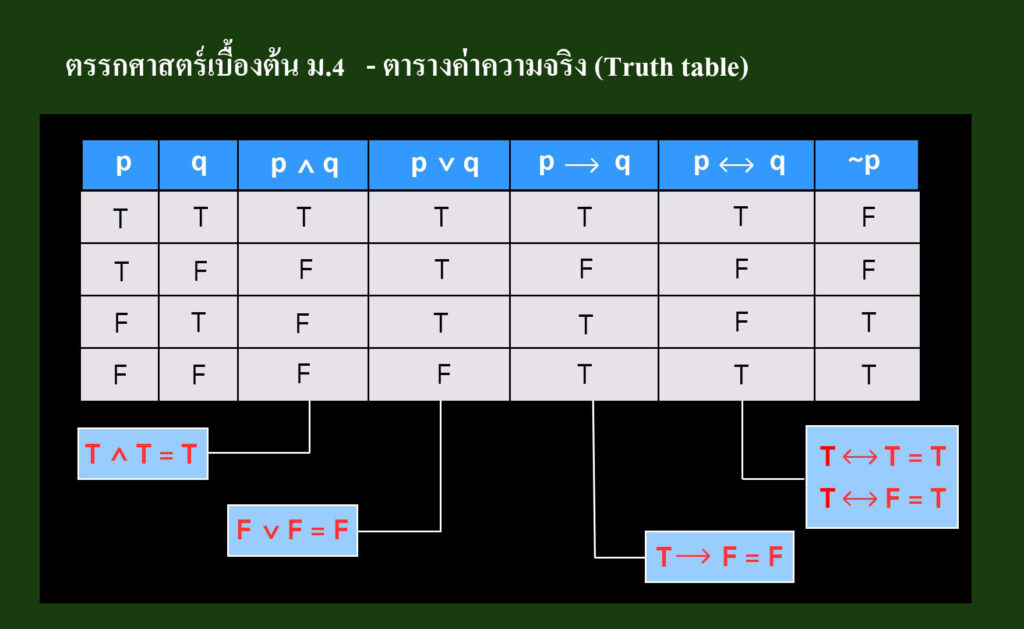
ตารางค่าความจริง (Truth table)

ประพจน์ที่เป็นนิเสธกัน

ประพจน์ 2 ประพจน์เป็นนิเสธกัน ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงตรงข้ามกันทุกกรณีของค่าความจริงของประพจน์ย่อย

ตัวอย่างประพจน์ที่เป็นนิเสธกันที่ควรทราบ มีดังนี้

~(p ∧ q) สมมูลกับ ~p ∨ ~q

~(p ∨ q) สมมูลกับ ~p ∧ ~q

~(p → q) สมมูลกับ p ∧ ~q

~(p ⇔ q) สมมูลกับ (p ⇔ ~q) ∨(q ⇔ ~p)

~(p ⇔ q) สมมูลกับ (p ∧ ~q) ∨ ( q ∧~p)

สัจนิรันดร์

สัจจะ แปลว่าจริง ส่วนนิรันดร์ แปลว่าตลอดกาล ประพจน์ที่เป็นสัจนิรันดร์ คือ ประพจน์ที่มีค่าความจริงเป็นจริง ทุกกรณีของประพจน์ย่อย

ประโยคเปิด (Open Sentence)

คือข้อความที่อยู่ในรูปประโยคบอกเล่าหรือปฏิเสธ ที่มีตัวแปรและสื่อแทนค่าของตัวแปรนั้น จะได้ค่าความจริงแน่นอน หรือเป็นประพจน์ นิยมใช้สัญลักษณ์ P(x), P(x , y), Q(x , y) แทนประโยคเปิดที่มีตัวแปรระบุในวงเล็บ

ตัวบ่งปริมาณ (∀,∃)

ตัวบ่งปริมาณ เป็นตัวระบุจำนวนสมาชิกในเอกภพสัมพัทธ์ที่ทำให้ประโยคเปิดกลายเป็นประพจน์ ตัวบ่งปริมาณมี 2 ชนิด คือ

ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกทุกตัวในเอกภพสัมพัทธ์” ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∀” อ่านว่า”สำหรับสมาชิก x ทุกตัว”

ตัวบ่งปริมาณที่กล่าวถึง “สมาชิกบางตัวในเอกภพสัมพัทธ์” ซึ่งเขียนแทนได้ด้วยสัญลักษณ์ “∃” อ่านว่า “สำหรับสมาชิก x บางตัว”

ค่าความจริงของประพจน์ที่มีตัวบ่งปริมาณ

∀x[P(x)] มีค่าความจริงเป็นจริง เมื่อ x ทุกตัวในเอกภพสัมพัทธ์ทำให้ P(x) เป็นจริง

∀x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อมี x อย่างน้อย 1 ตัวที่ทำให้ P(x) เป็นเท็จ

∃x[P(x)] มีค่าความจริงเป็นจริง เมื่อมี x อย่าน้อย 1 ตัวที่ทำให้ P(x) เป็นจริง

∃x[P(x)] มีค่าความจริงเป็นเท็จ เมื่อไม่มี x ใดๆ ในเอกภพสัมพัทธ์ที่ทำให้ P(x) เป็นจริง

นิเสธของประพจน์ที่มีตัวบ่งปริมาณ

~∀x[P(x)] สมมูลกับ ∃x[~P(x)]

~∃x[P(x)] สมมูลกับ∀x[~P(x)]

~∀x[~P(x)] สมมูลกับ∃x[P(x)]

~∃x[~P(x)] สมมูลกับ∀x[P(x)]

การอ้างเหตุผล

การอ้างเหตุผล คือ การอ้างว่า “สำหรับเหตุการณ์ P1, P2,…, Pn ชุดหนึ่ง สามารถสรุปผลที่ตามมา C ได้” การอ้างเหตุผลนี้ ได้รับเลือกเป็นตัวแทนของ ข้อสอบในเรื่องตรรกศาสตร์ ให้เป็นข้อสอบเข้ามหาวิทยาลัย อย่าง O-Net และ PAT1 บ่อยๆ จึงเป็นเรื่องที่สำคัญมาก

การอ้างเหตุผลประกอบด้วย 2 ส่วน คือ

เหตุ หรือสิ่งที่กำหนดให้

ผล หรือสิ่งที่ตามมา

สำหรับการพิจารณาว่า การอ้างเหตุผลนั้นสมเหตุสมผลหรือไม่นั้นพิจารณาได้จากประพจน์ ( P1 ∧ P2 ∧ … Pn) → C ถ้าประพจน์ดังกล่าวมีค่าความจริงเป็นจริงเสมอ (เป็นสัจนิรันดร์) เราสามารถสรุปได้ว่าการอ้างเหตุผลดังกล่าวเป็นการอ้างที่สมเหตุสมผล

ตัวอย่างเช่น

เหตุ 1. p → q

2. p

ผล q

สรุปการอ้างเหตุผลและตัวอย่าง

การอ้างเหตุผลคือ การอ้างว่า เมื่อมีประพจน์ p₁,p₂,…p_n, ชุดหนึ่ง แล้วสามารถสรุปประพจน์ C ประพจน์หนึ่งได้ การอ้างเหตุผลประกอบด้วยส่วนสำคัญสองส่วนคือ เหตุหรือสิ่งที่กำหนดให้ ได้แก่ ประพจน์ p₁,p₂,…p_n, และ ผลหรือข้อสรุป คือ ประพจน์ C โดยใช้ตัวเชื่อม ∧ เชื่อมเหตุทั้งหมด เข้าด้วยกัน และใช้ตัวเชื่อม → เชื่อมส่วนที่เป็นเหตุกับผลดังนี้

(p₁ ∧ p₂ ∧ … ∧ p_n,) → C

จะกล่าวว่า การอ้างเหตุผลนี้ สมเหตุสมผล (valid) ถ้ารูปแบบของประพจน์ (p₁ ∧ p₂ ∧ … ∧ p_n,) → C เป็นสัจนิรันดร์ และจะกล่าวว่า การอ้างเหตุผลนี้ ไม่สมเหตุสมผล (invalid) ถ้ารูปแบบของประพจน์ (p₁ ∧ p₂ ∧ … ∧ p_n,) → C ไม่เป็นสัจนิรันดร์ ดังนั้น ในการตรวจสอบความสมเหตุสมผลจึงใช้วิธีเดียว กับการตรวจสอบสัจนิรันดร์

ตัวอย่าง

กำหนดให้ p และ q เป็นประพจน์ จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ

p→q
p

ผล q

วิธีทำ ขั้นที่ 1 ใช้ ∧ เชื่อมเหตุเข้าด้วยกัน และใช้ → เชื่อมส่วนที่เป็นเหตุกับผล จะได้รูปแบบของประพจน์คือ [(p → q) ∧ p]→q

ขั้นที่ 2ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่ สมมติให้[(p → q) ∧ p]→q เป็นเท็จ

จากแผนภาพ แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ p]→q เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้สมเหตุสมผล

ตัวอย่าง

เหตุ

p→q
∼p

ผล ∼q

วิธีทำ ขั้นที่ 1 ใช้ ∧ เชื่อมเหตุเข้าด้วยกัน และใช้ → เชื่อมส่วนที่เป็นเหตุกับผล จะได้รูปแบบของประพจน์คือ [(p → q) ∧ ∼p]→∼q

ขั้นที่ 2ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่ สมมติให้[(p → q) ∧ ∼p]→∼q เป็นเท็จ

จากแผนภาพ มีกรณีที่ p เป็นเท็จ และ q เป็นจริง ที่ทำให้ [(p → q) ∧ ∼p]→∼q เป็นเท็จ

แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ ∼p]→∼q ไม่เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้ไม่สมเหตุสมผล

ตัวอย่าง

จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ

ถ้าฝนตกที่บ้านของสุชาดา แล้วหลังคาบ้านของสุชาดาเปียก
หลังคาบ้านของสุชาดาไม่เปียก

ผล ฝนไม่ตกที่บ้านของสุชาดา

วิธีทำ ให้ p แทนประพจน์ “ฝนตกที่บ้านของสุชาดา”

q แทนประพจน์ “หลังคาบ้านของสุชาดาเปียก”

เขียนแทนข้อความข้างต้นในรูปสัญลักษณ์ได้ดังนี้

เหตุ

p→q
∼q

ผล ∼p

ดังนั้น รูปแบบของประพจน์ในการอ้างเหตุผลนี้ คือ[(p → q) ∧ ∼q]→∼p

ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่

สมมติให้ [(p → q) ∧ ∼q]→∼p เป็นเท็จ

จากแผนภาพ แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ ∼q]→∼p เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้สมเหตุสมผล

ตัวอย่าง

จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ

ถ้าแป้งได้โบนัส แล้วแป้งจะฝากเงินกับธนาคาร 10,000 บาท
แป้งฝากเงินกับธนาคาร 10,000 บาท

ผล แป้งได้โบนัส

วิธีทำ ให้ p แทนประพจน์ “แป้งได้โบนัส”

q แทนประพจน์ “แป้งฝากเงินกับธนาคาร 10,000 บาท”

เขียนแทนข้อความข้างต้นในรูปสัญลักษณ์ได้ดังนี้

เหตุ

p→q
q

ผล p

ดังนั้น รูปแบบของประพจน์ในการอ้างเหตุผลนี้ คือ[(p → q) ∧ q]→p

ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่

สมมติให้ [(p → q) ∧ q]→ p เป็นเท็จ

จากแผนภาพ มีกรณีที่ p เป็นเท็จ และ q เป็นจริง ที่ทำให้[(p → q) ∧ q]→ p เป็นเท็จ

แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ q]→ p ไม่เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้ไม่สมเหตุสมผล

ตัวอย่าง

จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ

นุ่นซื้อรถคันใหม่ หรือ นุ่นลงทุนในตลาดหุ้น
นุ่นไม่ซื้อรถคันใหม่

ผล นุ่นลงทุนในตลาดหุ้น

วิธีทำ ให้ p แทนประพจน์ “นุ่นซื้อรถคันใหม่”

q แทนประพจน์ “นุ่นลงทุนในตลาดหุ้น”

เขียนแทนข้อความข้างต้นในรูปสัญลักษณ์ได้ดังนี้

เหตุ

p→q
∼p

ผล q

ดังนั้น รูปแบบของประพจน์ในการอ้างเหตุผลนี้ คือ[(p → q) ∧ ∼p]→ q

ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่

สมมติให้ [(p → q) ∧ ∼p]→ q เป็นเท็จ

จากแผนภาพ แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ ∼p]→ q เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้สมเหตุสมผล

ตัวอย่าง

จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ

ถ้าไฟฟ้าดับ แล้วโรงแรมต้องใช้เครื่องปั่นไฟ
ถ้าโรงแรมต้องใช้เครื่องปั่นไฟ แล้วลิฟต์จะทำงานไม่ได้

ผล ถ้าไฟฟ้าดับ แล้วลิฟต์จะทำงานไม่ได้

วิธีทำ ให้ p แทนประพจน์ “ถ้าไฟฟ้าดับ”

q แทนประพจน์ “โรงแรมต้องใช้เครื่องปั่นไฟ”

r แทนประพจน์ “ลิฟต์จะทำงานไม่ได้”

เขียนแทนข้อความข้างต้นในรูปสัญลักษณ์ได้ดังนี้

เหตุ

p→q
q→r

ผล p→r

ดังนั้น รูปแบบของประพจน์ในการอ้างเหตุผลนี้ คือ[(p → q) ∧ (q→r)]→ (p→r)

ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่

สมมติให้ [(p → q) ∧ (q→r)]→ (p→r) เป็นเท็จ

จากแผนภาพ แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ (q→r)]→ (p→r) เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้สมเหตุสมผล

ตัวอย่าง

จงพิจารณาว่าการอ้างเหตุผลต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ

ถ้าเก่งไปทำงาน แล้วก้องอยู่บ้าน
ถ้าก้องไม่อยู่บ้าน แล้วกล้าเป็นคนดูแลบ้าน
กล้าไม่ได้เป็นคนดูแลบ้าน

ผล เก่งไม่ได้ไปทำงาน

วิธีทำ ให้ p แทนประพจน์ “เก่งไปทำงาน”

q แทนประพจน์ “ก้องอยู่บ้าน”

r แทนประพจน์ “กล้าเป็นคนดูแลบ้าน”

เขียนแทนข้อความข้างต้นในรูปสัญลักษณ์ได้ดังนี้

เหตุ

p→q
q→r
∼r

ผล ∼p

ดังนั้น รูปแบบของประพจน์ในการอ้างเหตุผลนี้ คือ[(p → q) ∧ (q→r)∧∼r]→ ∼p

ตรวจสอบรูปแบบของประพจน์ที่ได้ว่าเป็นสัจนิรันดร์หรือไม่

สมมติให้ [(p → q) ∧ (q→r)∧∼r]→ ∼p เป็นเท็จ

จากแผนภาพ แสดงว่า รูปแบบของประพจน์ [(p → q) ∧ (q→r)∧∼r]→ ∼p ไม่เป็นสัจนิรันดร์

ดังนั้น การอ้างเหตุผลนี้ไม่สมเหตุสมผล

สรุปตรรกศาสตร์เบื้องต้น-คณิตศาสตร์ออนไลน์ ม.4

การเชื่อมประพจน์

ตารางค่าความจริง (Truth table)

Author: tmtyai

Related Posts