สรุปสูตรสถิติ ม.6 ตอนที่ 2 ท่องก่อนเรียนออนไลน์
สรุปสูตรสถิติ
การวัดตำแหน่งของข้อมูล (Measures of Position)
การวัดการกระจาย (Measures of Variability)
เป็นการหาค่าสถิติที่ใช้วัดการกระจายของคะแนนในกลุ่มเพื่อบอกให้ทราบว่าความสามารถของผู้เรียนในกลุ่มแตกต่าง
กันมากน้อยแค่ไหนถ้าการวัดการกระจายมีค่ามากแสดงว่าคะแนนของเด็กกลุ่มนั้นกระจายมาก และถ้าการวัดการกระจายมีค่า
น้อย แสดงว่าคะแนนของเด็กกระจายน้อย ถ้าการวัดการกระจาย มีค่าเป็น “ 0 ” แสดงว่าเด็กกลุ่มนั้นมีคะแนนไม่กระจายหรือ
ทุกคนได้คะแนนเท่ากัน วิธีวัดการกระจายที่นิยมใช้มี 3 ชนิด
1. พิสัย (Range) สัญลักษณ์ที่ใช้ คือ R
2. ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) สัญลักษณ์ที่ใช้คือ S.D. หรือ S
3. ความแปรปรวน (Variance) สัญลักษณ์ที่ใช้ คือ V
พิสัย
เป็นวิธีการวัดการกระจายที่ง่ายที่สุดหาได้จากความแตกต่างระหว่างคะแนนสูงสุดกับคะแนนต่ำสุดของข้อมูล ดังสมการ
พิสัย = คะแนนสูงสุด – คะแนนต่ำสุด
ตัวอย่าง นักเรียน 2 กลุ่ม กลุ่มละ 20 คน สอบได้คะแนนดังนี้
กลุ่มที่ 1 5,6,7,7,9,3,8,10,8,7,6,5,4,9,7,8,7,6,5,4 กลุ่มที่ 2 9,6,6,7,9,3,8,10,9,7,6,5,4,9,9,8,7,6,5,9
พิสัยกลุ่มที่ 1 = 10 – 3 = 7 พิสัยกลุ่มที่ 2 = 10 – 3 = 7
การใช้พิสัย
ค่าพิสัยของข้อมูลทั้งสองกลุ่มมีค่าเท่ากัน คือ 7 แต่การกระจายของข้อมูลที่เหลือในแต่ละกลุ่มไม่เหมือนกันดังนั้นนิยม
ใช้พิสัยในกรณีที่ต้องการดูการกระจายของข้อมูลอย่างรวดเร็ว หรือต้องการจะจัดทำตารางแจกแจงความถี่เท่านั้น
ส่วนเบี่ยงเบนมาตรฐาน
เป็นการวัดการกระจายที่ดี และใช้กันมากที่สุด มีประโยชน์ในการที่จะอนุมานค่าบางอย่างของข้อมูลแต่ละตัวจาก
ค่าเฉลี่ยมีสูตรพื้นฐานในการคำนวณดังนี้
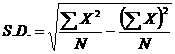
ตัวอย่าง คะแนนจากการสอบภาษาอังกฤษ 5 คน ได้คะแนนดังนี้ 3 5 9 10 12
จงหาความเบี่ยงเบนมาตรฐานของคะแนนชุดนี้
การใช้ส่วนเบี่ยงเบนมาตรฐาน
1. ใช้บอกสภาพการสอบของกลุ่มควบคู่กับค่าเฉลี่ย
2. ใช้หาค่าความแปรปรวน
ความแปรปรวน คือค่าเฉลี่ยของกำลังสองของผลต่างระหว่างค่าของข้อมูลแต่ละตัว
กับค่าเฉลี่ย หรือ ความแปรปรวนคือ กำลังสองของส่วนเบี่ยงเบนมาตรฐานสูตรพื้นฐานในการคำนวณมีดังนี้
ดังนั้นส่วนเบี่ยงเบนมาตรฐาน เท่ากับ 10.95 คะแนน
สรุปการเปรียบเทียบความแตกต่างระหว่างข้อมูล 2 กลุ่ม
การวัดการกระจาย (Measure of Dispersion)
การใช้สถิติเกี่ยวกับการวัดแนวโน้มเข้าสู่ส่วนกลาง ซึ่งเป็นค่าที่ทำ หน้าที่เป็นตัวแทนกลุ่มข้อมูล เพียงอย่างเดียว เมื่อแปลความหมายข้อมูลจึงยังไม่สมบูรณ์ ไม่ชัดเจน และ มีโอกาสคลาดเคลื่อนได้ สิ่งที่ ควรน3มาพิจารณาควบคู่ไปกับการวัดแนวโน้มเข้าสู่ส่วนกลางก็คือ ลักษณะการกระจายของกลุ่มข้อมูล ซึ่งสถิติที่ใช้คือ การวัดการกระจาย การที่ข้อมูลแต่ละชุดมีค่าต่าง ๆ กันนั้นเราเรียกว่า ข้อมูลมีการกระจาย ถ้าข้อมูลชุดนั้นประกอบ ด้วยค่าแตกต่างกันมาก เรียกว่า ข้อมูลมีการกระจายมาก ถ้าข้อมูลชุดนั้นประกอบด้วยค่าต่าง ๆ แตกต่าง กันน้อย หรือมีค่าใกล้เคียงกันเรียกว่า ข้อมูลมีการกระจายน้อย ถ้าข้อมูลนั้นประกอบด้วยค่าต่าง ๆ เท่ากัน หมด เรียกว่า ข้อมูลไม่มีการกระจาย
ข้อมูลชุดที่ 1 : 9 , 12 , 37 , 73 , 105
ข้อมูลชุดที่ 2 : 52 , 60 , 63 , 61 , 65
ข้อมูลชุดที่ 3 : 35 , 35 , 35 , 35 , 35
จากข้อมูลทั้ง 3 ชุด เมื่อเปรียบเทียบแล้วพบว่า ข้อมูลชุดที่ 1 มีการกระจายมากที่สุด ข้อมูลชุดที่ 2 มีการกระจายรองลงมา ส่วนข้อมูลชุดที่ 3 ไม่มีการกระจาย ในการเปรียบเทียบข้อมูลหลาย ๆ ชุดว่าแตกต่างกันหรือไม่ ควรจะต้องพิจารณาถึงค่าเฉลี่ย และ การกระจายของข้อมูลควบคู่กันไปด้วย เพื่อจะช่วยให้สรุปหรือแปลความหมายได้อย่างถูกต้อง เช่น เด็ก นักเรียนกลุ่มหนึ่งวัดคะแนนสอบวิชาภาษาไทยได้ 75 , 87 , 115 , 118 , 130 เด็กนักเรียนกลุ่มสองวัด คะแนนสอบวิชาภาษาไทยได้ 100 ,100 , 105 ,110 , 110 ค่าเฉลี่ยของคะแนน 2 ชุดนี้เท่ากัน คือ 105 ถ้าพิจารณาเฉพาะค่าเฉลี่ยจะสรุปได้ว่านักเรียน 2 กลุ่มนี้ มีคะแนนสอบวิชาภาษาไทยอยู่ในระดับเดียวกัน แต่เมื่อพิจารณาจากคะแนนแต่ละชุดจะพบว่าคะแนนสอบวิชาภาษาไทยของนักเรียนกลุ่มหนึ่งแตกต่าง กันมากกว่า คะแนนสอบวิชาภาษาไทยของนักเรียนในกลุ่มที่สอง นั่นคือ ตามข้อสรุปแล้วคะแนนสอบ วิชาภาษาไทยของนักเรียน 2 กลุ่มนี้แตกต่างกัน
ดังนั้น จึงสรุปได้ว่าถ้าต้องการบรรยายลักษณะของข้อมูล ให้ถูกต้องสมบูรณ์จะต้องวัดแนวโน้มเข้าสู่ส่วนกลางควบคู่ไปกับการวัดการกระจายด้วยเสมอ
การวัดการกระจาย แบ่งได้ 2 อย่าง
1.การวัดการกระจายสัมบูรณ์ (Absolute Variation)
เป็นการวัดการกระจายข้อมูลเพียงชุดเดียว มีดังนี้
1. พิสัย (Range : R)
2. ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation : S.D.,S,s)
พิสัย (Range : R)
พิสัย หมายถึง การหาการกระจายของข้อมูลโดยนำข้อมูลที่มีค่าสูงที่สุด ลบกับข้อมูลที่มีค่าต่ำที่สุด เพื่อให้ได้ค่าที่เป็นช่วงของการกระจาย ซึ่งสามารถบอกถึงความกว้างของข้อมูลชุดนั้นๆ สำหรับสูตรที่ใช้ในการหาพิสัยคือ
พิสัย (R) = Xmax – Xmin
ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation : S.D.,S,s)
ส่วนเบี่ยงเบนมาตรฐานเป็นค่าวัดการกระจายที่สำคัญทางสถิติ เพราะเป็นค่าที่ใช้บอกถึงการกระจายของข้อมูลได้ดีกว่าค่าพิสัย และค่าส่วนเบี่ยงเบนเฉลี่ย
การหาส่วนเบี่ยงเบนมาตรฐานสามารถหาได้ 2 วิธี
1.การหาส่วนเบี่ยงเบนมาตรฐาน(S.D.) ในกรณีข้อมูลไม่ได้มีการแจกแจงความถี่
สามารถหาได้จากสูตร
สูตรที่ 1
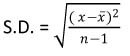
หรือ
สูตรที่ 2
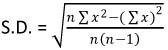
เมื่อ S.D. คือ ส่วนเบี่ยงเบนมาตรฐาน
คือ ข้อมูล ( ตัวที่ 1,2,3…,n)
คือ ค่าเฉลี่ยเลขคณิต
คือ จำนวนข้อมูลทั้งหมด
หมายเหตุในกรณีที่เป็นทศนิยมทำให้เกิดความยุ่งยากในการคำนวณ จึงควรเลือกใช้สูตรที่ 2
2.การหาส่วนเบี่ยงเบนมาตรฐาน(S.D.)ในกรณีข้อมูลมีการแจกแจงความถี่
สามารถหาได้จากสูตร
1. 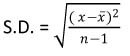 หรือ 2.
หรือ 2. 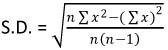
S.D. คือ ส่วนเบี่ยงเบนมาตรฐาน
คือ ความถี่
คือ จุดกึ่งกลางชั้น
คือ ค่าเฉลี่ยเลขคณิต
คือ จำนวนข้อมูล
2.การวัดการกระจายสัมพัทธ์ (relative Variation)
คือ การหาค่าเพื่อเปรียบเทียบการกระจายระหว่างข้อมูลมากกว่าหนึ่งชุด โดยใช้อัตราส่วน การเปรียบเทียบการกระจายของข้อมูลระหว่างชุดที่นิยมใช้มี 2 ชนิดคือ
1. สัมประสิทธิ์ของพิสัย(coefficient of range)
2.สัมประสิทธิ์ของการแปรผัน(coefficient of variation)
1. สัมประสิทธิ์ของพิสัย(coefficient of range) คือ อัตราส่วนระหว่างผลต่างของค่าสูงสุดและค่าต่ำสุด กับผลบวกของค่าสูงสุดและต่ำสุดของข้อมูลชุดนั้น
2. สัมประสิทธิ์ของการแปรผัน(coefficient of variation) ตัวย่อ(C.V.) อัตราส่วนระหว่างส่วนเบี่ยงเบนมาตรฐานกับค่าเฉลี่ยเลขคณิตของข้อมูลชุดนั้น
สูตร ![]()
เมื่อ C.V. คือ สัมประสิทธิ์ของการแปรผัน
s คือส่วนเบี่ยงเบนมาตรฐาน
![]() คือค่าเฉลี่ยเลขคณิต
คือค่าเฉลี่ยเลขคณิต
ค่าเฉลี่ยเลขคณิต(![]() ) จัดว่าเป็นค่าที่มีความสำคัญมากในวิชาสถิติ เพราะค่าเฉลี่ยเลขคณิตเป็นค่ากลางหรือเป็นตัวแทนของ ข้อมูลที่ดีที่สุด เพราะ
) จัดว่าเป็นค่าที่มีความสำคัญมากในวิชาสถิติ เพราะค่าเฉลี่ยเลขคณิตเป็นค่ากลางหรือเป็นตัวแทนของ ข้อมูลที่ดีที่สุด เพราะ
1)เป็นค่าที่ไม่เอนเอียง
2)เป็นค่าที่มีความคงเส้นคงวา
3)เป็นค่าที่มีความแปรปรวนต่ำที่สุด
4)เป็นค่าที่มีประสิทธิภาพสูงสุด แต่ค่าเฉลี่ยเลขคณิตก็มีข้อจำกัดในการใช้ เช่น ถ้าข้อมูลมีการกระจายมาก หรือข้อมูลบาง
ตัวมีค่ามากหรือน้อยจนผิดปกติ หรือข้อมูลมีการเพิ่มขึ้นเป็นเท่าตัว ค่าเฉลี่ยเลขคณิตจะไม่สามารถเป็นค่ากลางหรือเป็นตัวแทนที่ ดีของข้อมูลได้
การหาค่าเฉลี่ยเลขคณิตเมื่อข้อมูลไม่ได้มีการแจกแจงความถี่ (![]() ) ในกรณีที่ข้อมูลไม่ได้มีการแจกแจงความถี่ ค่าเฉลี่ย
) ในกรณีที่ข้อมูลไม่ได้มีการแจกแจงความถี่ ค่าเฉลี่ย
เลขคณิตสามารถหาได้โดย
สูตร 
เมื่อ xi แทนค่าสังเกตของข้อมูลลำดับที่ i
n แทนจำนวนตัวอย่างข้อมูล
นิยาม ค่าเฉลี่ยเลขคณิต คือ ผลรวมของค่าสังเกตหรือค่าของตัวอย่างที่ได้จากการสำรวจทุกค่าของข้อมูล แล้วหารด้วย


เครดิต : Arisara Panlam











