สรุปสูตรเรื่องฟังก์ชันตรีโกณมิติ-คณิตศาสตร์ ม.6

สรุปสูตรเรื่องฟังก์ชันตรีโกณมิติ

ฟังก์ชันตรีโกณมิติของผลบวกและผลต่าง

ใช้ในกรณีที่ต้องการแปลงค่ามุมให้เป็นมุมที่เราต้องการได้เพื่อประยุกต์ใช้ในกรณีต่าง ๆ

• cos(A-B) = cos(A)cos(B) + sin(A)sin(B)
• cos(A+B) = cos(A)cos(B) – sin(A)sin(B)
• sin(A+B) = sin(A)cos(B) + cos(A)sin(B)
• sin(A-B) = sin(A)cos(B) – cos(A)sin(B)
• tan(A+B) = (tan(A)+tan(B)) / (1-tan(A)tan(B))
• tan(A-B) = (tan(A)-tan(B)) / (1+tan(A)tan(B))

   

  

  

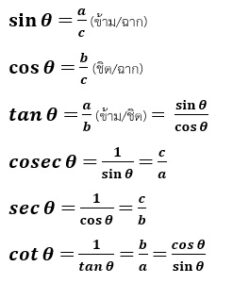
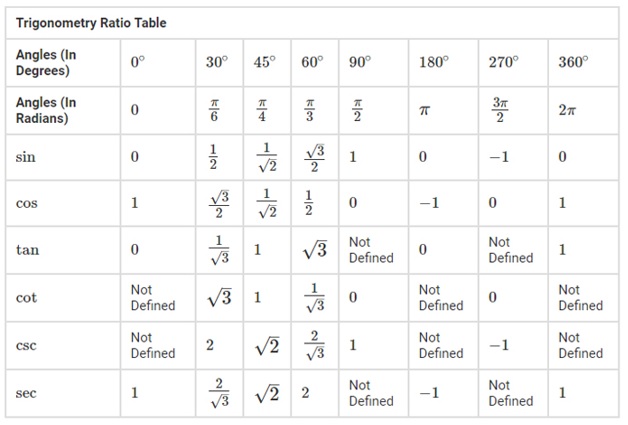
• ค่า sin⁡θ cos⁡θ tan⁡θ ของมุมพื้นฐานมีค่าเท่าไหร่บ้าง

•  

   

  ฟังก์ชันไซน์และโคไซน์

  การกำหนดค่าของฟังก์ชันตรีโกณมิตินั้น สามารถทำได้โดยการใช้วงกลมรัศมี 1 หน่วย มีจุดศูนย์กลางอยู่ที่จุดกำเนิดและเราจะเรียกวงกลมดังกล่าวว่า วงกลมหนึ่งหน่วย (The unit circle)

  เมื่อเรากำหนดจำนวนจริง θ (ทีตา) จาก (1,0) วัดระยะไปตามส่วนโค้งของวงกลม โดยมีข้อตกลงดังนี้ว่า :

  ถ้า θ > 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางทวนเข็มนาฬิกา

  ถ้า θ < 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางตามเข็มนาฬิกา

  ถ้า θ = 0 จุดปลายส่วนโค้งคือจุด (1,0)

  จะได้ว่า เมื่อเรากำหนดจำนวนจริง θ ให้ เราสามรารถหาจุด (x,y) ซึ่งเป็นจุดปลายส่วนโค้งได้เพียงจุดเดียวเท่านั้น

  ถ้า |θ| > 2π แสดงว่า วัดส่วนโค้งเกิน 1 รอบ เพราะเส้นรองวงของวงกลมยาว 2π หน่วย