สรุปสูตรเรื่องลอการิทึม (Logarithm function)

เรื่อง ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม

จากเรื่องฟังก์ชันเอกซ์โปเนนเชียล ถ้าให้ƒ แทนฟังก์ชันเอกซ์โปเนนเชียล ƒ จะมีลักษณะดังนี้

1. ƒ : R→R⁺

2. ƒ = {(x,y) : y = a^x , a > 0 , a≠1 }

เนื่องจากว่าฟังก์ชันเอกซ์โปเนนเชียลเป็นฟังก์ชันแบบหนึ่งต่อหนึ่ง (ค่า x หนึ่งค่า ให้ค่า y หนึ่งค่า)

ดังนั้น อินเวอร์สของฟังก์ชันเอกซ์โปเนนเชียลจึงเป็นฟังก์ชันหนึ่งต่อหนึ่งด้วย

ดังนี้

1. ƒ^-1 : R⁺→R

2. ƒ^-1 = {(x,y) : x = a^y , a > 0 , a≠1 }

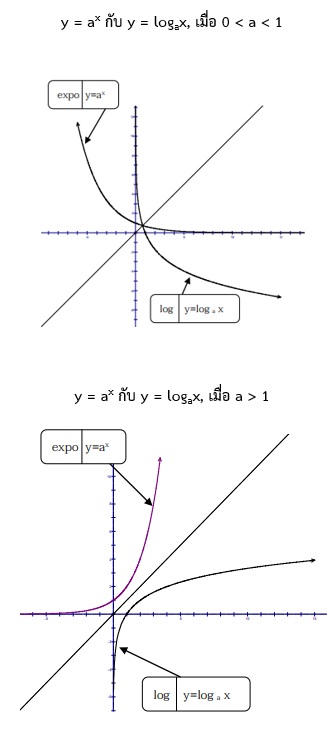
จาก x = a^yสามารถเขียนได้ในรูปของ y =ƒ^-1(x) โดยเราจะกำหนดสัญลักษณ์ได้เป็นy = log_ax (อ่านว่าลอการิทึมเอกซ์ฐานเอ หรือ ล็อกเอกซ์ฐานเอ)ดังนั้นฟังก์ชันอินเวอร์สของฟังก์ชันเอกซ์โปเนนเชียลจึงเขียนได้เป็น ƒ^-1 = {(x,y) : x = a^y , a > 0 , a≠1 }

ข้อสังเกตของกราฟในกรณี y = log_ax ; a > 0, a ≠1

1. กราฟของฟังก์ชันลอการิทึม จะตัดแกน y ที่คู่อันดับ(1, 0)

2. โดเมนของฟังก์ชันลอการิทึม คือเซตของจำนวนจริงบวก เรนจ์ของฟังก์ชันลอการิทึม คือเซตของจำนวนจริง

3. กรณีที่ a อยู่ในช่วง (1, ∞) แล้ว y = log_ax จะเป็นฟังก์ชันลด

กรณีที่ a อยู่ในช่วง(0, 1) แล้ว y = log_ax จะเป็นฟังก์ชันเพิ่ม

4.ฟังก์ชันลอการิทึม เป็นฟังก์ชัน 1-1 จาก R⁺ไปทั่วถึง R

นั่นคือ log_ax = log_ay ก็ต่อเมื่อ x = y

5. การเปรียบเทียบฟังก์ชันลอการิทึม

กรณี a อยู่ในช่วง(0, 1) เป็นฟังก์ชันลด จะได้ว่า

x > y ก็ต่อเมื่อ log_ax < log_ay

x < y ก็ต่อเมื่อ log_ax > log_ay

กรณี a อยู่ในช่วง(1,∞) เป็นฟังก์ชันเพิ่ม จะได้ว่า

x > y ก็ต่อเมื่อ log_ax > log_ay

x < y ก็ต่อเมื่อ log_ax < log_ay

การหาค่าลอการิทึมสามัญโดยใช้ตาราง

เนื่องจากในตารางระบุเพียงค่า
log 1 จนถึง log
9.99 เท่านั้น
หากต้องการหาค่า log N เราจะต้องเขียนจำนวน N เป็นรูป N₀×10ⁿเมื่อ 1≤ N₀ < 10 และใช้กฎของลอการิทึมว่า log N = log(N₀×10ⁿ) = log N₀ + n

เช่น log 1,150 มีค่าเท่ากับ log(1.15 ×10³)หรือ log(1.15) +3 จากตารางพบว่า log(1.15) ≈ 0.0607 ดังนั้น log 1,150 ≈ 3.0607

หมายเหตุ

1.หากค่า N₀ ในตารางไม่ละเอียดพอ ให้ประมาณค่าโดยเทียบสัดส่วนของระยะทาง

2. n จะเป็นจำนวนเต็มเสมอ
เรียกว่า แคแรกเทอริสติก (Characteristic) และ log N₀ จะมีค่าระหว่าง 0
ถึง 1 เสมอ เรียกว่า แมนทิสซา (Mantissa)
ของ log N

3.ตารางที่กำหนดให้ เป็นค่าลอการิทึมสามัญ (ฐาน 10) เท่านั้น ถ้าต้องการหาค่าลอการิทึมฐานอื่นๆ ต้องอาศัยกฎของลอการิทึมช่วยแปลงฐาน
นั่นคือ log_ab = log_cb ÷ log_ca และ ln b = log b ÷ log e

การหาค่าแอนติลอการิทึมโดยใช้ตาราง

จากตัวอย่างที่แล้ว เราทราบว่าค่า log ของ 1,150
เป็น 3.0607 (โดยประมาณ)
สามารถกล่าวแบบย้อนกลับได้ว่าค่า antilog ของ 3.0607 เป็น 1,150

ตัวอย่างเช่น ต้องการหาค่า M
ที่ทำให้ log M = 3.0607 เราต้องทำ
3.0607 ให้อยู่ในรูปผลบวกของแคแรกเทอริสติกกับแมนทิสซาก่อนนั่นคือ 3
+ 0.0607 จากนั้นเปิดตารางได้เป็น log10³+ log1.15 หรือ

log(1.15 ×10³) ดังนั้น M ≈ 1,150