สรุปเนื้อหาที่สำคัญความสัมพันธ์ และฟังก์ชัน คณิตศาสตร์ ม. 4
ความสัมพันธ์
ความสัมพันธ์ในทางคณิตศาสตร์นั้น มีความคล้ายกับความสัมพันธ์ในชีวิตจริงที่เราคุ้นเคย คือเป็นการแสดงความเกี่ยวข้องกันของสองสิ่ง ซึ่งในทางคณิศาสตร์เรียกว่า คู่อันดับ ซึ่งมีนิยามดังนี้
คู่อันดับ คือ การนำสิ่ง สองสิ่ง มาเขียนคู่กัน โดยคำนึงถึงลำดับด้วย ซึ่งเขียนได้ดังนี้
คู่อันดับ a, b เขียนแทนด้วย (a, b) โดยเรียก a ว่า สมาชิกตัวหน้าของคู่อันดับ และเรียก b ว่า สมาชิกตัวหลังของคู่อันดับ เช่น
การเท่ากันของคู่อันดับ หมายถึง (x1, y1) = (x2, y2)
ก็ต่อเมื่อ x1 = y1 และ x2 = y2 หรือก็คือ ตัวหน้า = ตัวหน้า, ตัวหลัง = ตัวหลัง
ตัวอย่างที่ 1 กำหนดให้ A = { a, b } จงหา A x P(A)
วิธีทำ พิจารณา P(A) = { { }, {a}, {b}, { a, b } } จะได้ว่า
A x P(A) = { (a, { }), (a, {a}), (a, {b}), (a, { a, b }), (b, { }), (b, {a}), (b, {b}), (b, { a, b }) }
ตัวอย่างที่ 2 ถ้า A และ B เป็นเซตที่มีจำนวนสมาชิกเท่ากับ 3 และ 5 ตามลำดับจำนวนความสัมพันธ์ของ A และ B ที่แตกต่างกันมีค่าเท่าใด
วิธีทำ เนื่องจาก n(A) = 3 และ n(B) = 5 จะได้ว่า n( A x B ) = 15 ความสัมพันธ์คือการเลือกหรือรวบรวมผลคูณคาร์ทีเซียนของ A และ B นั้นคือเซตย่อยของ A x B ดังนั้นจำนวนความสัมพันธ์ที่เป็นไปได้ทั้งหมดจะเท่ากับจำนวนเซตย่อยของ A x B เท่ากับ 215
ความสัมพันธ์ทวิภาค
ความสัมพันธ์ทวิภาคเป็นการรวบรวมสมาชิกของเซต 2 เซตที่สัมพันธ์กันอาจจะเป็นเซตเดียวกันหรือต่างเซตกันก็ได้ตัวอย่างเช่น กำหนดให้ A = {1,2,3,4,5} และ B = {2,4} การจับคู่กับระหว่างเซต A และ B หรือผลคูณคาร์ทีเซียน
A x B = { (1,2), (1,4), (2,2), (2,4), (3,2), (3,4), (4,2), (4,4), (5,2), (5,4) }
จะเห็นว่ามีการจับคู่ได้ทั้งหมด 10 แบบ แต่หากเราต้องการรวบรวมสมาชิกในเซต A และ B โดยที่สมาชิกในเซต A มีค่าน้อยกว่าสมาชิกในเซต B จาก A x B จะได้คู่อันดับ (1,2), (1,4), (2,4) และ (3,4) กำหนดใด้ R เป็นความสัมพันธ์ของเซต A และ B โดยที่สมาชิกในเซต A มีค่าน้อยกว่าสมาชิกในเซต B จะได้ว่า
R = { (1,2), (1,4), (2,4), (3,4) }
ให้ R1 เป็นความสัมพันธ์ระหว่างเซต A และเซต B โดยที่สมาชิกในเซต B หารสมาชิกในเซต A ได้ลงตัว
R1 = { (2,2), (4,2), (4,4) }
ให้ R2 เป็นความสัมพันธ์บนเซต A (ระหว่างเซต A และเซต A) โดยที่สมาชิกตัวค่าแรกมีค่าน้อยกว่าค่าที่ 2
R2 = { (1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,4), (3,4), (3,5), (4,5) }
เมื่อรู้จักคู่อันดับแล้ว ความสัมพันธ์ มีนิยามดังต่อไปนี้
ความสัมพันธ์ คือ เซตที่มีสมาชิกทุกตัวเป็นคู่อันดับ โดยที่คู่อันดับแต่ละคู่ เกิดจากการจับคู่กันของสมาชิกจากเซตสองเซต เช่น
- {(A, X), (B, Y), (C, Z), (D, W)}
- {(Galaxy Note 10, Samsung), (iPhone 11, Apple), (Find X, Oppo), …}
- {(1, 1), (2, 4), (3, 9), …}
ผลคูณคาร์ทีเชียน เป็นการกระทำกันระหว่างเซต 2 เซต โดยผลคูณคาร์ทีเชียนระหว่างเซต A และ B เขียนแทนด้วย A×B คือ เซตของคู่อันดับ (a,b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B เขียนอยู่ในรูปแบบดังนี้
A×B = {(a,b) | a ∈ A และ b ∈ B}
***ข้อสังเกต “ความสัมพันธ์ระหว่างเซต A,B ทุกอันต้องเป็นสับเซตของ A×B”***
สมบัติของผลคูณคาร์ทีเชียน ให้ A, B และ C เป็นเซตใด ๆ และ n(A) คือ จำนวนสมาชิกของเซต A
- A×{} = {}
- {}×A = {}
- A×(B∪C) = (A×B)∪(A×C)
- A×(B∩C) = (A×B)∩(A×C)
- A×(B-C) = (A×B) – (A×C)
- n(A×B) = n(A).n(B)
ความสัมพันธ์จาก A ไป B ให้ A และ B เป็นเซตใด ๆ แล้ว r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ AB เขียนได้ว่า
r = {(a,b) | (a,b) ∈ A×B}
กราฟของความสัมพันธ์
ในระบบแกนมุมฉาก เราสามารถจับคู่หนึ่งต่อหนึ่ง ระหว่างคู่อันดับของจำนวนจริง (x, y) กับพิกัดของจุดบนระนาบ โดยให้ x เป็นพิกัดแรก และ y เป็นพิกัดหลัง จากหลักการดังกล่าวทำให้เราสามารถเขียนกราฟของความสัมพันธ์ได้ดังนี้
บทนิยาม
ให้ R เป็นเซตของจำนวนจริง และ r เป็นสับเซตของ R× R กราฟของความสัมพันธ์ r คือ เซตของจุดบนระนาบ โดยที่แต่ละจุดแทนสมาชิกของความสัมพันธ์ R
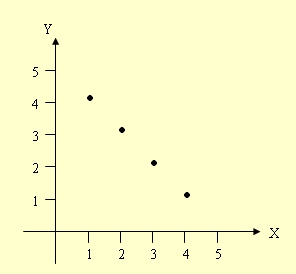
ตัวอย่างที่ 1
จงเขียนกราฟของความสัมพันธ์
r = { (x,y) ∈ A × A | x + y = 5} เมื่อกำหนดให้
A = {1, 2, 3, 4}
วิธีทำ
r = {(1, 4), (2, 3), (3, 2), (4, 1)}
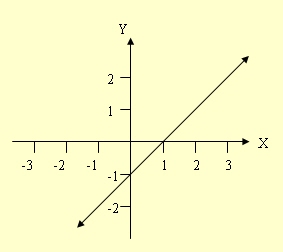
ตัวอย่างที่ 2
จงเขียนกราฟของความสัมพันธ์
r = { (x,y) ∈ R × R | y = x – 1}
วิธีทำ
ตัวอย่างที่ 3
จงเขียนกราฟของความสัมพันธ์
วิธีทำ
r = { (x,y) ∈ R × R | -1 < y ≤ 2 }
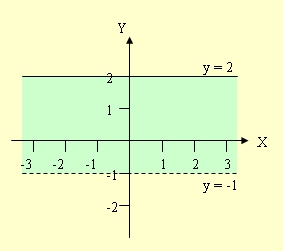
ตัวอย่างที่ 4
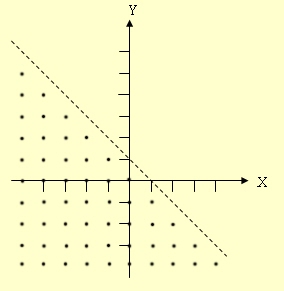
จงเขียนกราฟของความสัมพันธ์
วิธีทำ
r = { (x,y) ∈ I × I | x + y < 1 }