สรุปเนื้อหาย่อลำดับและอนุกรม ม.ปลาย

สรุปเนื้อหาย่อลำดับและอนุกรม ม.ปลาย

• อนุกรม คือ อะไร
• ลำดับ คือ อะไรบ้าง
•  ลําดับและอนุกรม มีอะไรบ้าง
• ลำดับจำกัด
• ลำดับอนันต์
• ลำดับเลขคณิต
• ลำดับเรขาคณิต
• ลำดับพหุนาม
• ลำดับหลายชั้น
• ลำดับเว้นระยะ
• ลำดับแบบมีค่าแตกต่างกันเป็นชุด
• ลำดับยกกำลัง
• ความสัมพันธ์เวียนเกิด
• ลําดับและอนุกรม สูตร ทั้งหมดที่ควรรู้

ลำดับและอนุกรม

ความหมายของลำดับในการเขียนลำดับ จะเขียนเฉพาะสมาชิกของเรนจ์เรียงกันไป กล่าวคือ ถ้า a เป็น ลำดับจำกัด จะเขียนแทนด้วย a1, a2, a3, …, an และถ้า a เป็น ลำดับอนันต์ จะเขียนแทนด้วย a1, a2, a3, …, an, …

เรียก a1 ว่า พจน์ที่ 1 ของลำดับ

เรียก a2 ว่า พจน์ที่ 2 ของลำดับ

เรียก a3 ว่า พจน์ที่ 3 ของลำดับ

และเรียก an ว่า พจน์ที่ n ของลำดับ หรือพจน์ทั่วไปของลำดับ

อนุกรม 

ลําดับและอนุกรม สรุป

อนุกรม ผลจากการบวกสมาชิกทุกตัวของลำดับไม่จำกัดเข้าด้วยกัน หากกำหนดให้ลำดับของจำนวนเป็นอนุกรมของลำดับนี้ก็คือ อนุกรมสามารถเขียนแทนได้ด้วย สัญลักษณ์ของผลรวม ∑ (ซิกม่า)

ลำดับ 

ลำดับ คือ ฟังก์ชันที่มีโดเมนเป็นเซตของจำนวนเต็มบวก n ตัวแรกหรือเซตของจำนวนเต็มบวกเรียกลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก n ตัวแรกว่า ลำดับจำกัดและเรียกลำดับที่มีโดเมนของจำนวนเต็มบวกว่า ลำดับอนันต์

ลำดับและอนุกรม ม.5

ลำดับ เป็นจำนวนหรือพจน์ที่เขียนเรียงกันภายใต้กฏเกณฑ์อย่างใดอย่างหนึ่งเป็นลำดับทั่ว ๆ ไป โดยแบ่งออกเป็น 2 ชนิด ได้แก่

– ลำดับจำกัด คือ ลำดับซึ่งมีจำนวนพจน์จำกัด เช่น 1, 2, 3, 4, …, 100 ฯลฯ
– ลำดับอนันต์ คือ ลำดับซึ่งมีจำนวนพจน์ไม่จำกัด เช่น 1, 2, 3, 4, … ฯลฯ

ลำดับ

บทนิยาม คือ ฟังก์ชันที่มีโดเมนเป็นเซตของจำนวนเต็มบวกที่เรียงจากน้อยไปมากโดยเริ่มตั้งแต่ 1 เรียกว่า “ลำดับ” ถ้าฟังก์ชันเป็นลำดับที่มีโดเมนเป็น { 1, 2, 3, …, n } เรียกว่า “ลำดับจำกัด” และถ้าฟังก์ชันเป็นลำดับที่มีโดเมนเป็น { 1, 2, 3, … } เรียกว่า “ลำดับอนันต์”

ลำดับ คือ กลุ่มของตัวเลขที่มีความสัมพันธ์กัน ซึ่งแบ่งออกเป็น 2 รูปแบบใหญ่ ๆ คือ

• ลำดับเลขคณิต
• ลำดับเรขาคณิต

ซึ่งลำดับเลขคณิตเป็นลำดับที่เกิดจากการบวก แต่ลำดับเรขาคณิตเป็นลำดับที่เกิดจากการคูณ

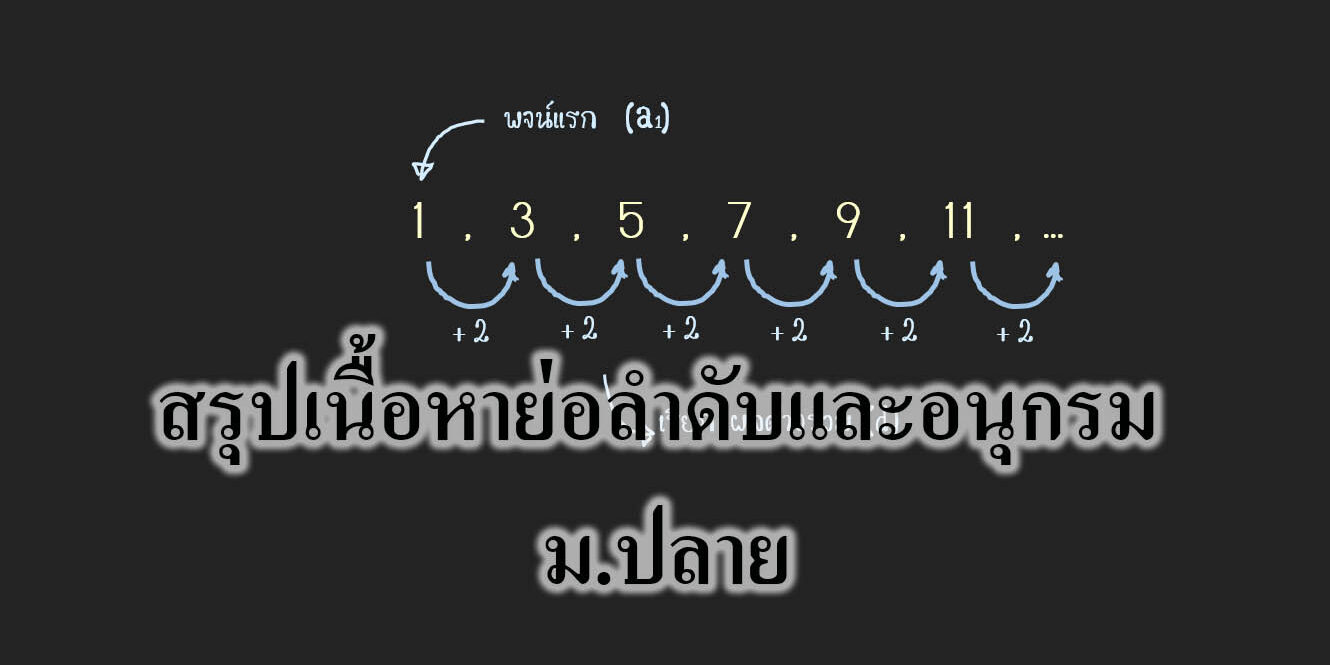
• ลำดับเลขคณิต คือ ลำดับที่มีผลต่างของพจน์ที่ n+1 กับพจน์ที่ n โดยมีค่าคงที่เป็นผลต่างร่วม (d)

ตัวอย่าง

1, 3, 5, 7, 9 ….  มี d = 2

9, 6, 3, 0, …. มี d = -3

อนุกรมที่ได้จากลำดับเลขคณิต เรียกว่า อนุกรมเลขคณิต และผลต่างร่วมของลำดับเลขคณิตเป็นผลต่างร่วมของอนุกรมเลขคณิตด้วย

เมื่อ a1, a1 + d, a1 + 2d, …, a1 + (n – 1)d เป็นลำดับเลขคณิต จะได้ a1 + (a1 + d) + (a1 + 2d) + … + (a1 + (n – 1)d) เป็นอนุกรมเลขคณิต ซึ่งมี a1 เป็นพจน์แรกของอนุกรม และ d เป็นผลต่างร่วมของอนุกรมเลขคณิต

จากบทนิยาม จะได้ว่า ถ้า a1, a2, a3, …, an เป็น ลำดับเลขคณิต ที่มี n พจน์ จะเรียกการเขียนแสดงผลบวกของพจน์ทุกพจน์ของลำดับในรูป a1 + a2 + a3 + … + an ว่า อนุกรมเลขคณิต และผลต่างร่วม (d) ของลำดับเลขคณิต เป็นผลต่างร่วมของอนุกรมเลขคณิตด้วย

• ลำดับเรขาคณิต คือ ลำดับที่มีอัตราส่วนของพจน์ที่ n+1 กับพจน์ที่ n โดยมีค่าคงที่เป็นอัตราส่วนร่วม (r)

ตัวอย่าง

3, 6, 12, 24 …. มี r = 2

2, -4, 8, -16 … มี r = -2

• วิธีการหา a ที่พจน์ใดๆ
  • ลำดับเลขคณิต :  a_n=a₁+(n-1)d
  • ลำดับเรขาคณิต : a_n=a₁r^n-1

อนุกรมที่ได้จากลำดับเรขาคณิต เรียกว่า อนุกรมเรขาคณิต และอัตราส่วนร่วมของลำดับเรขาคณิตจะเป็นอัตราส่วนร่วมของอนุกรมเรขาคณิตด้วย

เมื่อ a1, a1r, a1r2, …, a1r n-1 เป็นลำดับเรขาคณิต จะได้ a1 + a1r + a1r2 + … + a1r n-1 เป็นอนุกรมเรขาคณิต ซึ่งมี a1 เป็นพจน์แรก และ r เป็นอัตราส่วนร่วมของอนุกรมเรขาคณิต

จากบทนิยาม จะได้ว่า ถ้า a1, a2, a3, …, an เป็น ลำดับเรขาคณิต ที่มี n พจน์ จะเรียกการเขียนแสดงผลบวกของพจน์ทุกพจน์ของลำดับในรูป a1 + a2 + a3 + … + an ว่า อนุกรมเรขาคณิต และอัตราส่วนร่วมของลำดับเรขาคณิต จะเป็นอัตราส่วนร่วมของอนุกรมเรขาคณิตด้วย