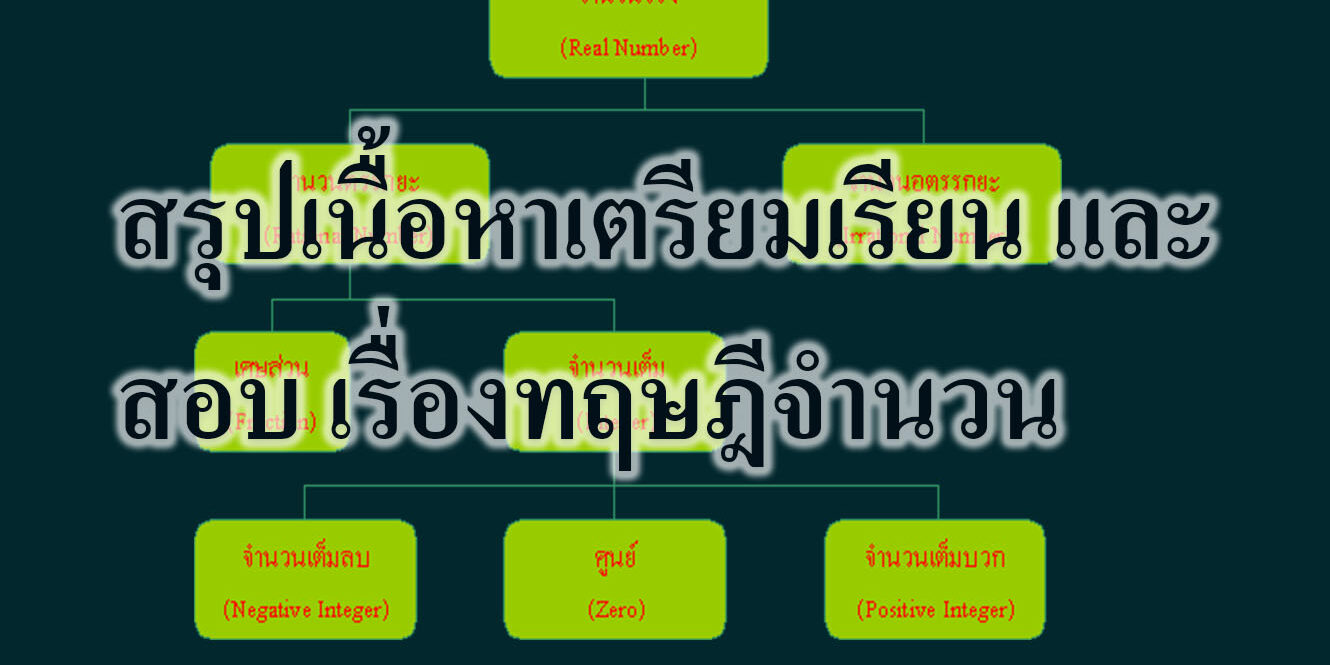
สรุปเนื้อหาเตรียมสอบ เรื่อง ทฤษฎีจำนวน
สรุปเนื้อหาที่สำคัญ
– การหารลงตัว
– จำนวนเฉพาะ
– ขั้นตอนวิธีการหาร
– การแปลงเลขฐาน
– การหารร่วมมาก
– ตัวคูณร่วมน้อย
สมบัติการหารลงตัว
ทฤษฎีบทที่ 1 กำหนด a, b, c เป็นจำนวนเต็มใดๆ
ถ้า a | b และ b | c แล้วจะได้ a | c
ทฤษฎีบทที่ 2 กำหนด a, b เป็นจำนวนเต็มบวก
ถ้า a | b แล้วจะได้ a ≤ b
ทฤษฎีบทที่ 3 กำหนด a, b, c เป็นจำนวนเต็มใดๆ
ถ้า a | b และ b | c แล้วจะได้ a | bx + cy
เมื่อ x, y เป็นจำนวนเต็มใดๆ
การจำแนกจำนวนเต็มบวกโดยใช้สมบัติการหารลงตัว
1.จำนวนเฉพาะ (Prime Numbers)
บทนิยาม จำนวนเต็ม p จะเป็นจำนวนเฉพาะ ก็ต่อเมื่อ p ≠ 0, p ≠ 1, p ≠ -1 และถ้ามีจำนวนเต็มที่หาร p
ลงตัว จำนวนเต็มนั้นต้องเป็นสมาชิกของ {-1, 1, p, -p}
2.จำนวนประกอบ (Composite Numbers)
บทนิยาม จำนวนเต็ม c เป็นจำนวนเต็มบวกที่มากกว่า 1 จะเป็นจำนวนประกอบ ก็ต่อเมื่อ c ไม่ใช่จำนวนเฉพาะ
นั่นคือสำหรับจำนวนเต็มบวก c ใดๆ c จะเป็นจำนวนประกอบ ก็ต่อเมื่อ มีจำนวนเต็ม m และ n ที่ต่างจาก c
ที่ทำให้ c = mn
ตัวอย่างเช่น
จำนวนที่หาร 2 ลงตัว ได้แก่ {-1, 1, 2, -2} ∴ 2 เป็นจำนวนเฉพาะ
จำนวนที่หาร 3 ลงตัว ได้แก่ {-1, 1, 3, -3} ∴ 3 เป็นจำนวนเฉพาะ
จำนวนที่หาร 4 ลงตัว ได้แก่ {-4, -2, -1, 1, 2, 4} ∴ 4 ไม่เป็นจำนวนเฉพาะ
จำนวนเฉพาะ
“จำนวนเฉพาะ” หรือ ไพรม์ นัมเบอร์ (Prime number) คือ จำนวนธรรมชาติที่มีตัวหารที่เป็นบวกอยู่ 2 ตัว คือ 1 กับตัวมันเอง เช่น 2, 3, 5, 7, 11, 13 และ 17 เป็นต้น และสำหรับเลข 1 นั้น ให้ตัดทิ้ง เพราะ 1 ไม่เป็นจำนวนเฉพาะ เซตของจำนวนเฉพาะทั้งหมดมักเขียนแทนด้วย เนื่องจาก 2 เป็นจำนวนเฉพาะตัวเดียวที่เป็นเลขคู่ ดังนั้นคำว่า จำนวนเฉพาะคี่ จะถูกใช้เพื่อหมายถึงจำนวนเฉพาะทั้งหมดที่ไม่ใช่ 2วิธีการหาจำนวนเฉพาะ
สมมติเขาถามว่า 331 เป็นจำนวนเฉพาะรึเปล่า ทุกคนก็คงจะเริ่มด้วยการประมาณค่ารากที่สองของ 331 ซึ่งได้ประมาณเกือบ ๆ 18 จากนั้นก็เริ่มเอาจำนวนเฉพาะไปหาร 331 ดู โดยเริ่มจาก 2 3 5 7 ไปเรื่อย ๆ แต่พอเราลองไปจนถึง 17 แล้วยังไม่มีจำนวนเฉพาะสักตัวหาร 331 ลงตัว เราก็หยุดและสรุปว่า 331 เป็นจำนวนเฉพาะ โดยไม่ต้องลองเอาจำนวนเฉพาะอื่นๆ ไปหาร 331 อีกต่อไป มีวิธีคิดดังนี้คือ ให้ n เป็นจำนวนนับใด ๆ (n เป็นจำนวนเฉพาะหรือไม่ก็เป็นจำนวนประกอบเพียงอย่างใดอย่างหนึ่ง)
– สมมติว่า n เป็นจำนวนประกอบ
– จำนวนประกอบคือจำนวนที่มีจำนวนอื่นนอกจาก 1 และตัวมันเองที่หารมันลงตัว
– ดังนั้นมีจำนวนนับ a โดย a หาร n ลงตัว และ 1 < a < n
– นั่นคือจะมีจำนวนนับ b ที่ 1 < b < n และ n = a * b
– โดยไม่เสียนัยสำคัญกำหนดให้ a <= b (ถ้า a > b ก็ให้สลับค่า a กับ b)
– สังเกตว่า a = รากที่สองของ (a^2) <= รากที่สองของ (a*b) = รากที่สองของ n
ขั้นตอนวิธีการหาร
• ขั้นตอนวิธีการหาร
ถ้า a และ b เป็นจำนวนเต็ม โดยที่ b ≠ 0 แล้วจะมี q และ r ซึ่งเป็นจำนวนเต็มที่ทำให้
a = bq + r เมื่อ 0 r |b|
นั่นคือ a เป็นตัวตั้งหารด้วย b ได้ผลหารคือ q และเศษ r
ตัวอย่างที่ 1
กำหนด a = 48, b = 7 จงหา q และ r
เขียนให้อยู่ในรูป
a = bq + r
48 = 7 × 6 +6
∴q = 6 และ r = 6
การแปลงฐานสองเป็นเลขฐานสิบ :
หลักการ : คือการเอาค่า Weight ของทุกบิตที่มีค่าเป็น 1 มาบวกกัน ดังตัวอย่าง
ตัวอย่าง : จงแปลง (11011101)2 ให้เป็นเลขฐานสิบ
(11011101)2 = (1X27) + (1X26) + (0X25) + (1X24) + (1X23)+ (1X22) +(0X21) + (1X20)
= 128 + 64 + 0 + 16 + 8 + 4 + 0 + 1
ผลลัพธ์ = (221)10
การเปลี่ยนเลขฐานสิบเป็นเลขฐานสอง
หลักการ
1. ให้นำเลขฐานสิบเป็นตัวตั้งและนำ 2 มาหาร ได้เศษเท่าไรจะเป็นค่าบิตที่มีนัยสำคัญน้อยที่สุด (LSB)
2. นำผลลัพธ์ที่ได้จากข้อที่ 1 มาตั้งหารด้วย 2 อีกเศษที่จัดจะเป็นบิตถัดไปของเลขฐานสอง
3. ทำเหมือนข้อ 2 ไปเรื่อยๆ จนได้ผลลัพธ์เป็นศูนย์ เศษที่ได้จะเป็นบิตเลขฐานสองที่มีนัยสำคัญมากที่สุด (MSB)
ตัวอย่าง : จงเปลี่ยน (221)10 เป็นเลขฐานสอง
2 221 เศษ 1 (LSB)
2 110 เศษ 0
2 55 เศษ 1
2 27 เศษ 1
2 13 เศษ 1
2 6 เศษ 0
2 3 เศษ 1
2 1 เศษ 1 (MSB)
0
\ (221)10 = (11011101)2
การเปลี่ยนเลขฐานแปดเป็นฐานสิบและเลขฐานสิบเป็นฐานแปด
การเปลี่ยนเลขฐานแปดเป็นเลขฐานสิบ
หลักเกณฑ์ : นำค่าน้ำหนัก (Weight)และเลขฐานแปดคูณด้วยเลข
ประจำหลักแล้วนำผลที่ได้ทุกหลักมารวมกัน
น้ำหนัก : Weight ได้แก่ … 84 83 82 81 80 8-1 8-2 8-3…
ตัวอย่าง : (134)8 = (…)10
(134)8 = (1X82) + (3X81) + (4X80)
= 64 + 24 + 4
= (92) 10
ดังนั้น (134)8 = (92)10
จุดทศนิยม
การเปลี่ยนเลขฐานสิบเป็นเลขฐานแปด
หลักเกณฑ์ : นำเลขฐานสิบเป็นตัวตั้งแล้วหารด้วย 8 เศษที่ได้จากการ
หารจะเป็นค่าของเลขฐานแปด ทำเช่นเดียวกับการเปลี่ยน
เลขฐานสิบเป็นฐานสอง
ตัวอย่าง : (92)10 = (…)8
8 92 เศษ 4
8 11 เศษ 3
8 1 เศษ 1
0
1 3 4
ดังนั้น (92)10 = (134)8
การเปลี่ยนเลขฐานแปดเป็นสองและเลขฐานสองเป็นฐานแปด
การเปลี่ยนเลขฐานแปดเป็นเลขฐานสอง
หลักการ : จะต้องใช้เลขฐานสิบเป็นตัวกลางในการเปลี่ยน
ตัวอย่าง : (134)8 = (…)2
1. เปลี่ยนเลขฐานแปดเป็นเลขฐานสิบ
(134)8 = (1X88) + (3X81) + (4X80)
= (92)10
2. เปลี่ยนเลขฐานสิบเป็นเลขฐานสอง
(92)10 = (…)2
Weight = 64 32 16 8 4 2 1
= 64 + 0 + 16 + 8 + 4 + 0 + 0
เลขฐาน 2 = 1 0 1 1 1 0 0
ดังนั้น (134)8 = (1011100)2
การเปลี่ยนเลขฐานสองเป็นเลขฐานแปด
หลักการ : จะต้องใช้เลขฐานสิบเป็นตัวกลางในการเปลี่ยน
ตัวอย่าง : (1011100)2 = (…)8
1. 1. เปลี่ยนเลขฐานสองเป็นเลขฐานสิบ
(1011100)2 = 64 + 0 + 16 + 8 + 4 + 0 + 0
= (92)10
2. 2. เปลี่ยนฐานสิบเป็นเลขฐานแปด
8 92 เศษ 4
8 11 เศษ 3
8 1 เศษ 1
0
1 3 4
ดังนั้น (1011100)2 = (134)8
การเปลี่ยนเลขฐานสองเป็นเลขฐานแปดและฐานแปดเป็นเลขฐานสอง วิธีลัด
|
เลขฐานแปด |
เลขฐานสอง |
|
0 1 2 3 4 5 6 7 |
000 001 010 011 100 101 110 111 |
ตารางเปรียบเทียบเลขฐานแปดและเลขฐานสอง
จากตารางจะเห็นว่าเลขฐานแปดหนึ่งหลักสามารถแทนด้วยเลขฐานสองจำนวน 3 บิต
ตัวอย่าง : จงแปลงเลขฐานสองเป็นเลขฐานแปด
(1011100) 2 = (…)8
วิธีทำ : 001 011 100
1 3 4
ดังนั้น (1011100) 2 = (134)8
ตัวอย่าง เปลี่ยนเลขฐานแปดเป็นเลขฐานสอง
(6143)8 = (…)2
วิธีทำ 6 1 4 3
110 001 100 011
ดังนั้น (6143)8 = (110001100011)2
การเปลี่ยนเลขฐานสิบหกเป็นฐานสิบและเลขฐานสิบเป็นฐานสิบหก
การเปลี่ยนเลขฐานสิบหกเป็นเลขฐานสิบ
หลักการ : นำค่าน้ำหนัก (Weight) ของเลขฐานสิบหกคูณด้วยเลขประจำ
หลัก และนำผลที่ได้ทุกหลักมารวมกัน
น้ำหนัก (Weight) : … 164 163 162 161 160 16-1 16-2 16-3…
ตัวอย่าง (6C)16 = (…)10
(6C)16 = (5X161) + (12X160)
= 80 + 12
= (92)10
ดังนั้น (6C)16 = (92)10
ตัวอย่าง (0.3)16 = (…)10
(0.3)16 (0.3)16 = 3X10-1
= 3X0.0625
= (0.1875)10
ดังนั้น (0.3)16 = (0.1878)10
การเปลี่ยนเลขฐานสิบเป็นเลขฐานสิบหก
หลักการ : นำเลขฐานสิบมาเป็นตัวตั้งแล้วนำ 16 มาหาร เศษที่ได้จากการหาร จะเป็นค่า
เลขฐานสิบหก ทำเช่นเดียวกับการเปลี่ยนเลขฐานสิบเป็นเลขฐานสอง
ตัวอย่าง : (92)10 = (…)16
วิธีทำ : 16 92 เศษ 12 =C
16 5 เศษ 5
5 C
ดังนั้น (92)10 = (5C)16
ตัวอย่าง (0.7875)10 = (….)16
วิธีทำ
| ผลการคูณ |
ผลของจำนวนเต็ม |
| 0.7875 X 16 = 12.6
0.6 X 16 = 9.6 |
12 = C 9 |
| 0.6 X 16 = 9.6
0.6 X 16 = 9.6 |
9 9 |
ดังนั้น (0.7875)10 = (0.C9)16
หารร่วมมาก(ห.ร.ม)
ห.ร.ม. บางทีเรียกว่า หารร่วมมาก หมายถึง ตัวหารร่วมที่มีค่ามากที่สุด
ห.ร.ม. จะเกิดขึ้นเมื่อมีจำนวนนับตั้งแต่ 2 จำนวนขึ้นไป
การหาร ห.ร.ม. สามารถหาได้หลายวิธี ดังนี้
วิธีที่ 1 วิธีหาตัวประกอบ มีขั้นตอนดังนี้
1) หาตัวประกอบของจำนวนนับที่กำหนดให้
2) หาตัวประกอบร่วม (ตัวหารร่วม) ของจำนวนนับในข้อ 1
3) นำตัวหารร่วมที่มีค่ามากที่สุดในข้อ 2 เป็น ห.ร.ม.
ตัวอย่าง จงหา ห.ร.ม.ของ 12 , 18
ตัวประกอบของ 12 คือ 1 , 2 , 3 , 4 ,6 , 12
ตัวประกอบของ 18 คือ 1 , 2 , 3 , 6 , 9 ,18
ตัวประกอบร่วมของ 12 และ 18 คือ 1 , 2 , 3 , 6
ดังนั้น ห.ร.ม. ของ 12 และ 18 คือ 6
วิธีที่ 2 วิธีแยกตัวประกอบ มีขั้นตอนดังนี้
1) แยกตัวประกอบของจำนวนนับที่กำหนดให้
2) พิจารณาผลในข้อ 1 ว่ามีจำนวนใดซ้ำกันทุกบรรทัดบ้าง
3) นำจำนวนที่ซ้ำกันในข้อ 1 คูณกัน
4) ผลคูณที่ได้จากข้อ 3 เป็น ห.ร.ม.
ตัวอย่าง จงหา ห.ร.ม.ของ 12 , 18
12 = 2 x 2 x 3
18 = 2 x 3 x 3
ดังนั้น ห.ร.ม. ของ 12 และ 18 คือ 2 x 3 = 6
คูณร่วมน้อย(ค.ร.น)
ค.ร.น. บางทีเรียกว่า คูณร่วมน้อย หมายถึง ตัวคูณร่วมที่มีค่าน้อยที่สุด
ค.ร.น.. จะเกิดขึ้นเมื่อมีจำนวนนับตั้งแต่ 2 จำนวนขึ้นไป
การหาร ค.ร.น.สามารถหาได้หลายวิธี ดังนี้
วิธีที่ 1 วิธีหาตัวประกอบ มีขั้นตอนดังนี้
1) หาว่าจำนวนนับที่กำหนดมาให้เป็นตัวประกอบของจำนวนใดบ้าง
2) หาตัวคูณร่วมของข้อ 1
3) นำตัวคูณร่วมที่มีค่าน้อยที่สุดในข้อ 2 เป็น ค.ร.น.
ตัวอย่าง จงหา ค.ร.น. ของ 12 , 18
12 เป็นตัวประกอบของ 12 , 24 , 36 , 48 , 60 , 72 , …
18 เป็นตัวประกอบของ 18 , 36 , 54 , 72 , 90 , …
ตัวคูณร่วมของ 12 และ 18 คือ 36 ,72 , …
ดังนั้น ค.ร.น.. ของ 12 และ 18 คือ 36