สรุปเนื้อหาเรื่อง จำนวนจริง

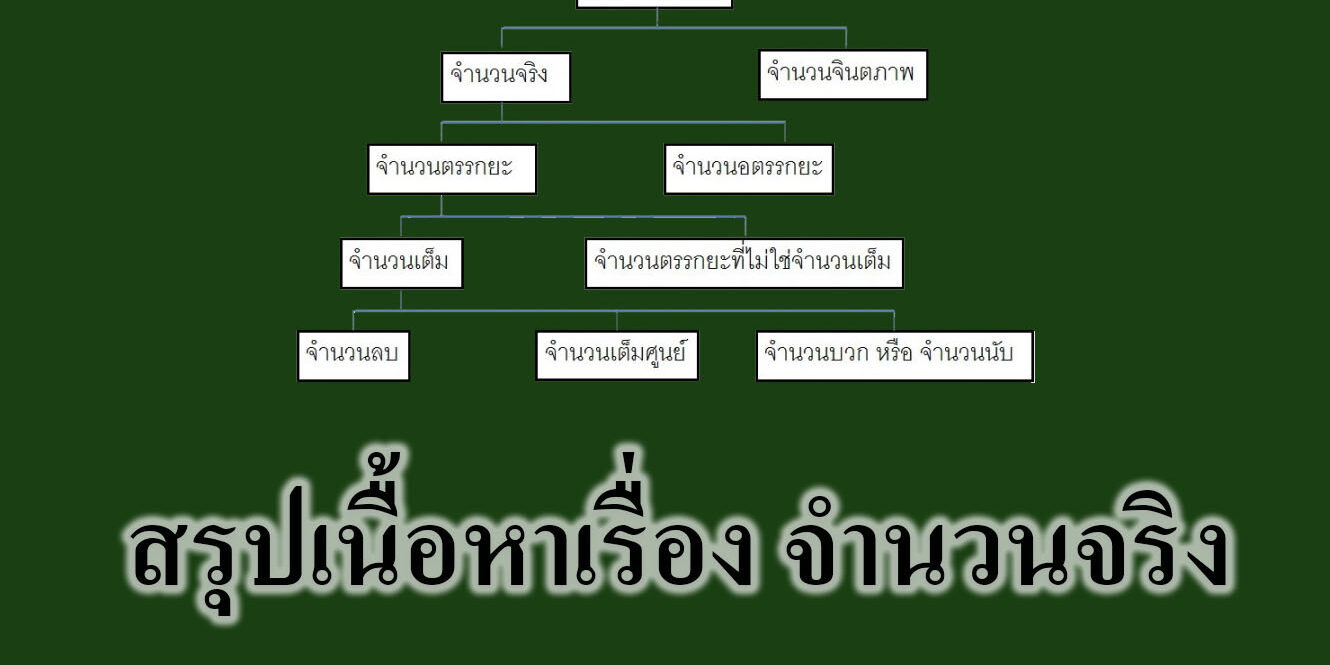
จำนวนอตรรกยะ

จำนวนอตรรกยะคือจำนวนที่มีความหมายตรงกันข้ามกับจำนวนตรรกยะ

จำนวนตรรกยะ (Rational Number) คือ จำนวนที่สามารถเขียนในรูปเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็มโดยที่ b ¹ 0 จำนวนตรรกยะ จำแนกได้เป็น 3 ประเภทใหญ่ ๆ คือ

ตัวอย่างของจำนวนอตรรกยะ เช่น จำนวนที่ติดอยู่ในค่าราก และไม่สามาถที่จะถอดค่ารากออกมาได้ เช่น

2√,3√,5√,7√32,3,5,73     เป็นต้น

ทศนิยม ที่ไม่ใช่ ทศนิยมซ้ำ เช่น

0.23456543…,2.34543…,34.5678943…,34,45432411…0.23456543…,2.34543…,34.5678943…,34,45432411…  เป็นต้น

จำนวนนอตรรกยะ ตัวหนึ่งที่น่าสนใจคือ  π π   ซึ่งเป็นอัตราส่วนระหว่างความยาวของเส้นรอบรูปวงกลมกับความยาวของเส้นผ่านศูนย์กลางของวงกลม

ข้อควรรู้

1. ถ้าจำนวนหนึ่งเป็นจำนวนอตรรกยะแล้ว  แล้วจำนวนตรงข้ามกับจำนวนนั้นจะเป็นจำนวนนอตรรกยะด้วย เช่น

2√2  เป็นจำนวนอตรรกยะ  จะได้ว่าจำนวนตรงข้ามของ  2√2   คือ

−2√−2  เป็นจำนวนอตรรกยะด้วยเช่นกัน

ππ  เป็นจำนวนอตรรกยะ จะได้ว่าจำนวนตรงข้ามของ  ππ   คือ  −π−π  เป็นจำนวนอตรรกยะด้วยเช่นกัน

2. จำนวนอตรรกยะ มีสมบัติปิดสำหรับการบวก นั้นคือ ถ้านำจำนวนอตรรกยะมาบวกกัน ค่าทีได้จากการบวกจะเป็นจำนวนอตรรกยะเหมือนเดิมครับ  ตัวอย่างเข่น  π+π=2ππ+π=2π   ซึ่ง  2π2π  เป็นจำนวนอตรรกยะ

 

จำนวนตรรกยะ

จำนวนตรรกยะ (หรือเศษส่วน) คืออัตราส่วนของจำนวนเต็มสองจำนวน มักเขียนอยู่ในรูปเศษส่วน a/b เมื่อ a และ b เป็นจำนวนเต็ม และ b ไม่เท่ากับศูนย์

จำนวนตรรกยะแต่ละจำนวนสามารถเขียนได้ในรูปแบบที่หลากหลาย ตัวอย่างเช่น 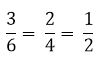 รูปแบบที่เรียกว่า เศษส่วนอย่างต่ำ a และ b นั้น a และ b จะต้องไม่มีตัวหารร่วม และจำนวนตรรกยะทุกจำนวนสามารถเขียนได้ในรูปเศษส่วนอย่างต่ำนี้

• • จำนวนเต็ม
    • จำนวนเต็มลบ
    • จำนวนเต็มศูนย์
    • จำนวนเต็มบวก
  • ไม่ใช่จำนวนเต็ม

จำนวนอตรรกยะ คือ จำนวนที่ไม่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็ม หรือทศนิยมซ้ำได้

จำนวนตรรกยะ คือ จำนวนที่สามารถเขียนให้อยู่ในรูปเศษส่วนของจำนวนเต็มหรือทศนิยมซ้ำได้ แบ่งได้เป็น

• จำนวนตรรกยะที่ไม่ใช่จำนวนเต็ม เช่น -1.5, 3,22/7
• จำนวนตรรกยะที่เป็น
  • จำนวนเต็มบวก เช่น 1, 2, 3, 4, 5, … , 7/7 , 14/7
  • จำนวนเต็มศูนย์ เช่น 0, 0/5
  • จำนวนเต็มลบ เช่น -1 , -2, -3, -4, …, – 7/7 , – 14/7

 

สมบัติของจำนวนจริง

กำหนด a, b, c เป็นจำนวนจริงใดๆ

 

สมบัติการเท่ากัน (=)

• สมบัติการสะท้อน a = a
• สมบัติการสมมาตร ถ้า a = b แล้ว b = a
• สมบัติการถ่ายทอด ถ้า a = b และ b = c แล้ว a = c
• สมบัติการบวกด้วยจำนวนที่เท่ากัน ถ้า a = b แล้ว a + c = b + c
• สมบัติการคูณด้วยจำนวนที่เท่ากัน ถ้า a = b แล้ว ac = bc

 

สมบัติการบวก (+)

• สมบัติปิด ถ้า a ϵ R และ b ϵ R แล้ว a + b ϵ R
• สมบัติการสลับที่ จะได้ a + b = b + a
• สมบัติการเปลี่ยนกลุ่ม จะได้ a + (b + c) = (a + b) + c
• สมบัติมีเอกลักษณ์การบวก คือ 0 จะได้ 0 + a = a + 0 = a
• สมบัติมีอินเวอร์สการบวก a มีอินเวอร์สการบวกคือ -a และ -a มีอินเวอร์สการบวก คือ a จะได้ a + (-a) = (-a) + a = 0

 

สมบัติการคูณ (.)

• สมบัติปิด ถ้า a ϵ R และ b ϵ R แล้ว a.b ϵ R
• สมบัติการสลับที่ จะได้ a.b = b.a
• สมบัติการเปลี่ยนกลุ่ม จะได้ a.(b.c) = (a.b).c
• สมบัติมีเอกลักษณ์การคูณ คือ 1 จะได้ 1.a = a.1 = a
• สมบัติมีอินเวอร์สการคูณ (ยกเว้น 0 เพราะ 1/0 ไม่มีความหมาย) a มีอินเวอร์สการคูณคือ 1/a และ 1/a มีอินเวอร์สการคูณ คือ a จะได้ a. 1/a = 1/a .a=1