สรุปเนื้อหาเรื่อง ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม

ฟังก์ชันเอกซ์โพเนนเชียล คือ ฟังก์ชันที่เขียนอยู่ในรูป {(x, y) ∈ $\mathbb{R}$ × $\mathbb{R}$ : y = a^x } โดยที่ a เป็นจำนวนจริงที่มากกว่า 0 และ a ≠ 1 เช่น 2^x , 1.2^x, 3^-x , 1.5^-xซึ่งพูดอีกอย่างก็คือ จำนวนจริงที่มีเลขชี้กำลังเป็นตัวแปรนั่นเอง

ฟังก์ชันเอกซ์โพเนนเชียล คือ f = { (x, y) ∈ R × R⁺ / y = a^x , a > 0, a ≠ 1 }

ฟังก์ชันเพิ่มและฟังก์ชันลด

f เป็นฟังก์ชันเพิ่ม เมื่อ

a > 1

เมื่อ a มากกว่า 1 และเมื่อ x เพิ่มขึ้นเรื่อยๆ จะทำให้ ค่าของ f เพิ่มขึ้นเรื่อยๆ ทำให้ f เป็นฟังก์ชันเพิ่ม

f เป็นฟังก์ชันลด เมื่อ

0 < a < 1

เมื่อ a อยู่ระหว่าง 0 กับ 1 เช่น 0.5, 0.3 เมื่อ x เพิ่มขึ้นเรื่อยๆ ค่าของ f จะลดลงเรื่อยๆ ทำให้ f เป็นฟังก์ชันลด

เมื่อ a > 1 ค่า a ยิ่งมากขึ้นกราฟจะยิ่งชัน

เมื่อ 0 < a < 1 ค่า a ยิ่งน้อย กราฟจะยิ่งชัน

การแก้อสมการเอกซ์โพเนนเชียล

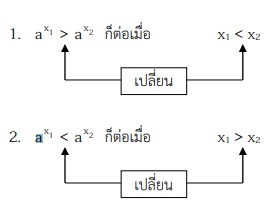
1. ถ้า 0 < a < 1 (ฟังก์ชันลด) แล้ว

สังเกตได้ว่า : สําหรับ 0 < a < 1 เมื่อปลดฐานหรือเติมฐาน เปลี่ยนเครื่องหมายอสมการ

ถ้า a > 1(ฟังก์ชันเพิ่ม) แล้ว

a^x1 > a^x2 ก็ต่อเมื่อ x₁ < x₂

a^x1 < a^x2 ก็ต่อเมื่อ x₁ > x₂

2. ถ้า a > 1 (ฟังก์ชันเพิ่ม) แล้ว

ถ้า a > 1(ฟังก์ชันเพิ่ม) แล้ว

a^x1 > a^x2 ก็ต่อเมื่อ x₁ > x₂

a^x1 < a^x2 ก็ต่อเมื่อ x₁ < x₂

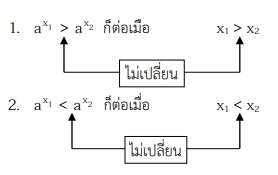
จุดสังเกต : สําหรับ a > 1 เมื่อปลดฐาน หรือเติมฐาน คงเดิมเครื่องหมายอสมการ

ฟังก์ชันลอการิทึม คืออะไร

ฟังก์ชันอินเวอร์สของฟังก์ชันเอกซ์โพเนนเชียลสามารถเขียนใหม่ได้เป็น { (x, y) ∈ R⁺ ×R / y = log_ax, a > 0, a ≠ 1 }
ฟังก์ชันอินเวอร์สของฟังก์ชันเอกซ์โพเนนเชียล ถูกเรียกใหม่ว่า ฟังก์ชันลอการิทึม
log_ax อ่านว่า “ลอการิทึมเอกซ์ฐานเอ” หรือ “ล็อกเอกซ์ฐานเอ”