สรุปเนื้อหาเรื่อง เรขาคณิตวิเคราะห์และภาคตัดกรวย
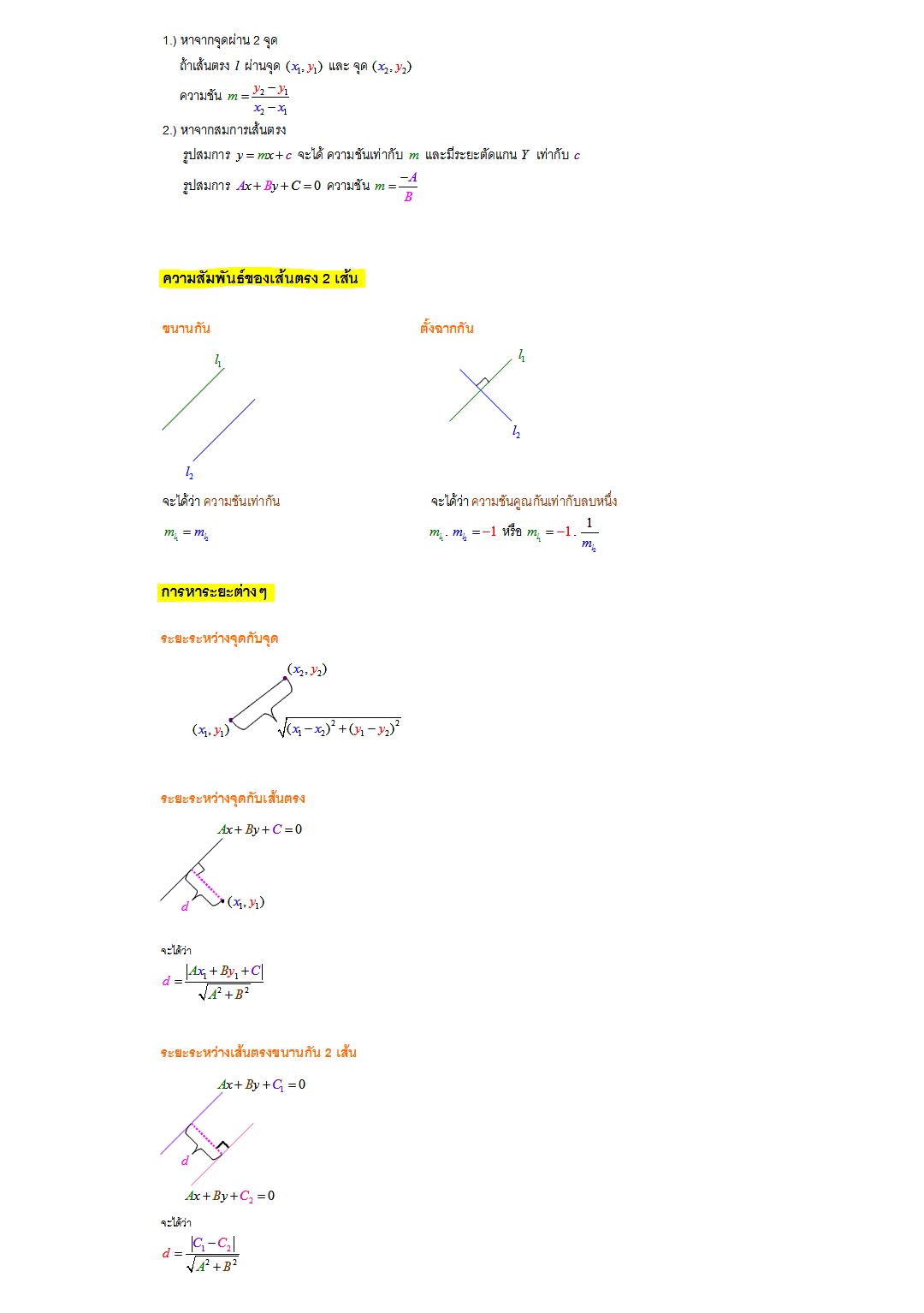
- ความชันของเส้นตรง (Slope : m)
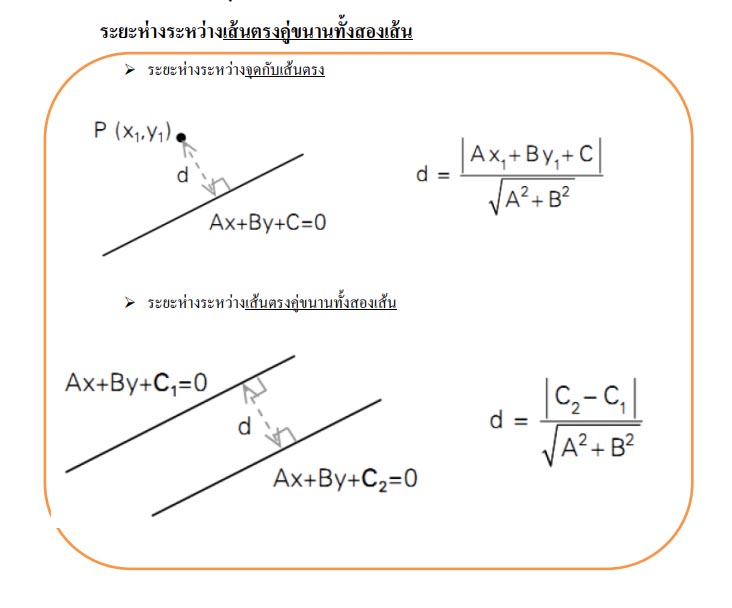
- เส้นขนานและเส้นตั้งฉาก
- ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง
- ภาคตัดกรวย (conic section หรือ conic)
- วงกลม
- สมการวงกลม
- วงรี
- สมการวงรี
- พาราโบลา
- ไดเรกตริกซ์
- สมการพาราโบลา
เนื้อหาหลักของบทนี้ประกอบด้วย รายละเอียดบทย่อย ดังนี้
- ความรู้เบื้องต้นเกี่ยวกับเรขาคณิตวิเคราะห์
- ระยะทางระหว่างจุดสองจุด
- จุดกึ่งกลางระหว่างจุดสองจุด
- ความชันของเส้นตรง
- เส้นขนาน
- เส้นตั้งฉาก
- ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง
- ระยะห่างระหว่างเส้นตรงกับจุด
- ภาคตัดกรวย
- วงกลม
- วงรี
- พาราโบลา (Parabola)
- ไฮเพอร์โบลา (Hyperbola)
- การเลื่อนกราฟ
เส้นตรง
เส้นตรง มีสมการรูปแบบทั่วไปคือ Ax + By + C = 0 และสมการรูปแบบมาตรฐานของเส้นตรงจะเขียนอยู่ในรูป y = mx + C ซึ่งจะอยู่ในหัวข้อ “สมการเส้นตรง” เส้นตรงหนึ่งเส้นประกอบไปด้วยจุดหลายจุด ซึ่งจุดเหล่านี้จะทำให้เราสามารถหาความชันได้ และเมื่อเราทราบความชันก็จะสามารถหาสมการเส้นตรงได้นั่นเอง
ความชันของเส้นตรง
ความชันของเส้นตรง ส่วนใหญ่นิยมใช้ m แทนความชัน การหาความชันนั้นเราจะต้องรู้จุดบนเส้นตรงอย่างน้อย 2 จุด
สมมติ ให้สองจุดนั้นเป็น (x1,y1) และ (x2,y2) เป็นจุดบนเส้นตรง L ดังรูป
จะได้ว่า ความชันของเส้นตรง L หาได้จาก
ความชันของเส้นตรง (Slope : m)
m = (y2 – y1) / (x2 – x1)
ความชันของเส้นตรง (Slope : m)
คือ อัตราส่วนระหว่างค่า y ที่เปลี่ยนแปลงไป ต่อค่า x ที่เปลี่ยนแปลงไป ใช้ สัญลักษณ์ m โดยค่า m อาจะเป็นบวก หรือลบ หรือเป็นศูนย์ก็ได้
- ถ้า m>0 แสดงว่า เส้นตรงนี้เฉียงขึ้นทางขวา
- ถ้า m<0 แสดงว่า เส้นตรงนี้เฉียงลงทางขวา
- ถ้า m=0 แสดงว่า เป็นเส้นนอนขนานแกน x
- ส่วนเส้นตั้งขนานกับแกน y นั้น m หาค่าไม่ได้ (เป็นอนันต์)
