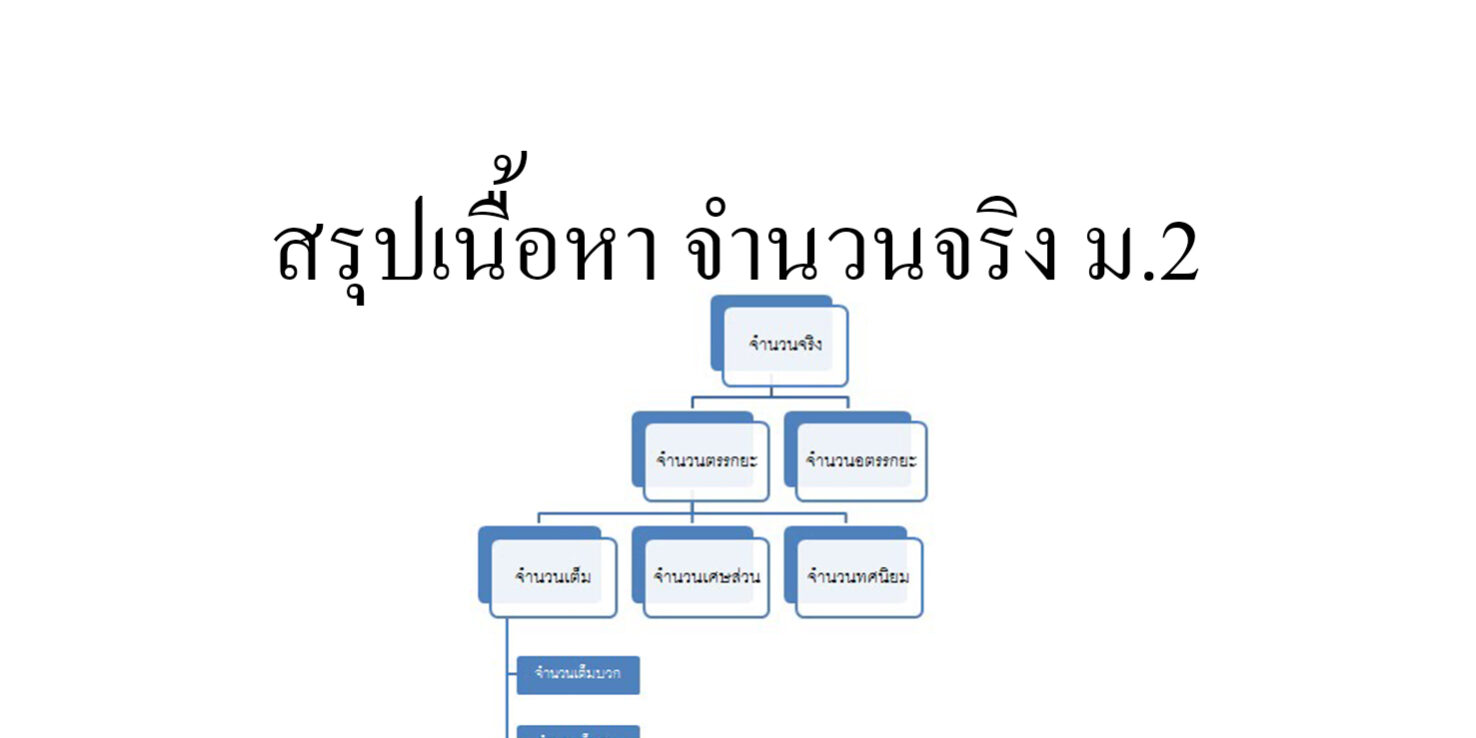
ระบบจำนวนจริง (Real number)
จํานวนจริงสามารถแบ่งได้เป็น 2 ลักษณะ คือ จํานวนตรรกยะ และจํานวนอตรรกยะ
1.จำนวนตรรกยะ (Rational Number) หมายถึง จำนวนที่สามารถเขียนได้ในรูป เศษส่วน
ของจำนวนเต็ม (ตัวส่วนไม่เท่ากับ 0 ) หรือเป็นทศนิยมซ้ำ เช่น 12,−35,227,−6,0.3,0.43˙8˙,7.643,36
จำนวนตรรกยะ (Rational Numbers) คือจำนวนที่สามารถเขียนในรูปเศษส่วนได้เมื่อเศษและส่วนเป็นจำนวนเต็มและ “ส่วนมีค่าไม่เท่ากับ 0 ”
ได้แก่ จำนวนเต็ม เศษส่วน และทศนิยมซ้ำ
1.1) จำนวนเต็ม (Integer Numbers) คือ จำนวนที่ไม่มีเศษส่วน และทศนิยมรวมอยู่ในจำนวนนั้น ประกอบด้วย
1.1.1) จำนวนเต็มบวก ( I+ )หรือจำนวนนับ คือ จำนวนเต็มที่มีค่ามากกว่า 0 ไปเรื่อย ๆ โดยที่ไม่สามารถระบุได้ว่าจำนวนนับตัว สุดท้ายเป็นอะไร จำนวนนับเริ่มต้นที่ 1 , 2 , 3, … ซึ่งเราทราบแล้วว่า จำนวนนับที่น้อยที่สุด คือ 1 จำนวนนับที่มากที่สุดหาไม่ได้
1.1.2) จำนวนเต็มศูนย์ สมาชิกมีเพียงจำนวนเดียวคือ 0 ศูนย์เป็นจำนวนเต็มอีกชนิดหนึ่ง ที่เราไม่ถือว่าเป็นจำนวนนับจาก
หลักฐานที่ค้นพบทำให้เราทราบว่ามนุษย์รู้จักใช้สัญลักษณ์ “0″ ในราวปี ค.ศ. 800 โดยที่ “0″ แทนปริมาณของการไม่มีของหรือของที่ต้องการ
กล่าวถึงแต่ก็ไม่ใช่ว่า 0 จะไม่มีความหมายถึงการไม่มีเสมอไป ตัวอย่าง เช่น ระดับผลการเรียนทางด้านความรู้ โดยนักเรียนที่มีระดับผลการเรียน เป็น 0 ไม่ได้หมายความว่านักเรียนคนนั้นไม่มีความรู้ เพียงแต่ว่ามีความรู้ในระดับหนึ่งเท่านั้น
1.1.3) จำนวนเต็มลบ ( I–) คือ จำนวนที่มีค่าน้อยกว่า ศูนย์ มีตำแหน่ง อยู่ทางด้านซ้ายมือของศูนย์เมื่ออยู่บนเส้นจำนวน
และจะมีค่าลดลงเรื่อย ๆ โดยไม่สามารถจะบอกได้ว่าจำนวนใดจะมีค่าน้อยที่สุด แต่เราสามารถรู้ได้ว่าจำนวนเต็มลบที่มีค่ามากที่สุด คือ –1
2. จำนวนอตรรกยะ (Irrational Number ) หมายถึง จำนวนที่ไม่สามารถเขียนในรูป
เศษส่วนของจำนวนเต็มหรือเป็นทศนิยมไม่รู้จบ เช่น
จำนวนอตรรกยะ ในวิชาคณิตศาสตร์ คือจำนวนที่ไม่สามารถเขียนได้ในรูปเศษส่วนที่มีทั้งตัวเศษและส่วนเป็นจำนวนเต็มได้ หรือกล่าวได้ว่ามันไม่สามารถเขียนในรูป a/b ได้ เมื่อ a และ b เป็นจำนวนเต็ม และ b ไม่เท่ากับศูนย์ เห็นได้ชัดว่าจำนวนอตรรกยะคือ จำนวนที่ไม่ว่าเขียนทศนิยมในฐานใดก็ตามจะไม่รู้จบ และไม่มีรูปแบบตายตัว แต่นักคณิตศาสตร์ก็ไม่ได้ให้นิยามจำนวนอตรรกยะเช่นนั้น จำนวนจริงเกือบทั้งหมดเป็นจำนวนอตรรกยะโดยนัยที่จะอธิบายต่อไปนี้
จำนวนอตรรกยะบางจำนวนเป็นจำนวนพีชคณิต เช่น รากที่สองของ 2 3 รากที่สามของ 5 และสัดส่วนทอง แทนด้วยอีกษรกรีก (ฟาย) หรือบางครั้ง (เทา) ที่เหลือเป็นจำนวนอดิศัย เช่น π และ e
เช่น  มีค่าประมาณ 1.414
มีค่าประมาณ 1.414
 มีค่าประมาณ 1.732
มีค่าประมาณ 1.732
π = 3.14159265… มีค่าประมาณ 3.142
 มีค่าประมาณ 0.707
มีค่าประมาณ 0.707
ตัวอย่าง
จำนวนเต็มยังสามารถแบ่งได้อีกเป็น 3 ประเภทด้วยกัน
1. จำนวนเต็มลบ หมายถึง จำนวนที่เป็นสมาชิกของเซต I – โดยที่ I – = {…, -4, -3, -2, -1}
เมื่อ I – เป็นเซตของจำนวนเต็มลบ
2. จำนวนเต็มศูนย์ (0)
3. จำนวนเต็มบวก หมายถึง จำนวนที่เป็นสมาชิกของเซต I+ โดยที่ I+ = {1, 2, 3, 4, …}
เมื่อ I+ เป็นเซตของจำนวนเต็มบวก
จำนวนเต็มบวก เรียกได้อีกอย่างว่า “จำนวนนับ” ซึ่งเขียนแทนเซตของจำนวนนับได้ด้วยสัญลักษณ์ N โดยที่ N = I+ = {1, 2, 3, 4, …}
ระบบจำนวนเชิงซ้อนนอกจากระบบจำนวนจริงที่กล่าวมาข้างต้นแล้ว ยังมีจำนวนอีกประเภทหนึ่ง ซึ่งได้จากการแก้สมการต่อไปนี้
x^2 = -1 ∴ x = √-1 = i
x^2= -2 ∴ x = √-2 = √2 i
x^2 = -3 ∴ x = √-3 = √3 i
จะเห็นได้ว่า “ไม่สามารถจะหาจำนวนจริงใดที่ยกกำลังสองแล้วมีค่าเป็นลบ” เราเรียก √-1 หรือจำนวนอื่นๆ ในลักษณะนี้ว่า “จำนวนจินตภาพ”และเรียก i ว่า “หนึ่งหน่วยจินตภาพ” เขียนแทนด้วยสัญลักษณ์ i
ยูเนียนของเซตจำนวนจริงกับเซตจำนวนจินตภาพ คือ ” เซตจำนวนเชิงซ้อน ” (Complex numbers)