สรุปเรื่อง ซับเซตและเพาเวอร์เซต ( subset and power set)

ซับเซตและเพาเวอร์เซต ( subset & power set)

สับเซต (Subset) หรือ เซตย่อย

ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B

ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ B เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B

ตัวอย่าง การเป็นสับเซตและไม่เป็นสับเซตกัน

กำหนดให้ A={1,2,3,4,5},B={2,3,5} และ C={2,4}

จะเห็นว่าสมาชิกทุกตัวของ B คือ 2,3 และ 5 เป็นสมาชิกของ A ด้วย ดังนั้น B ⊂ A และสมาชิกของ C คือ 2 และ 4 ก็เป็นสมาชิกของ A ด้วยเช่นกัน ดังนั้น C ⊂ A แต่ในขณะที่สมาชิกของ C ตัวหนึ่ง คือ 4 ไม่เป็นสมาชิกของ B ดังนั้น C ⊄ B

เพิ่มเรื่อง สับเซต หรือ เซตย่อย

การที่เราจะบอกว่า เซต A เป็นสับเซต(subset)ของเซต B ได้นั้น สมาชิก “ทุกตัวของ A” จะต้องเป็นสมาชิกของ B ด้วย เขียนแทนด้วย A ⊂ B

ตัวอย่างเช่น A = {1,3,5,7} , B = {1,2,3,4,5,6,7,8,9}

เราจะสังเกตเห็นว่า สมาชิกทุกตัวของ A เป็นสมาชิกของ B ดังนั้น A เป็นสับเซตของ B (A⊂B) แต่ B ไม่เป็นสับเซตของเซต A (B ⊄ A) เพราะ สมาชิกบางตัวของB ไม่อยู่ใน A

เราอาจจะวาดรูปเพื่อให้เข้าใจมากขึ้น

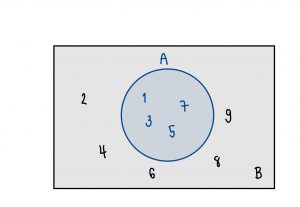
จากรูป เราจะเห็นได้ชัดเลยว่า สมาชิกทุกตัวของเซต A อยู่ในเซต B แต่สมาชิกบางตัวของเซต B ไม่อยู่ในเซต A

และเรายังสามารถบอกได้อีกว่า Ø, {1}, {3}, {5}, {7} ⊂ A และ Ø, {1}, {2}, {3} {4}, {5}, {6}, {7}, {8}, {9}⊂ B

**ข้อควรรู้ เซตว่าง(Ø)เป็นสับเซตของทุกเซต**

สับเซตแท้และสับเซตไม่แท้

สับเซตแท้ : ให้ A และ B เป็นเซตที่ A ⊂ B ถ้าจำนวนสมาชิก(หรือขนาด)ของ A ไม่เท่ากับจำนวนสมาชิกของ B จะได้ว่า A เป็นสับเซตแท้ของเซต B

สับเซตไม่แท้ : ให้ A และ B เป็นเซตที่ A ⊂ B ถ้าจำนวนสมาชิก(หรือขนาด)ของ A เท่ากับจำนวนสมาชิกของ B จะได้ว่า A ไม่เป็นสับเซตแท้ สามารถเขียนแทนด้วย A⊆B

สมบัติของสับเซต

1) A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)

2) A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)

3) ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)

4) ถ้า A ⊂ ø แล้ว A = ø

5) ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)

6) A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A

7) ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต

เพาเวอร์เซต(Power set)

ให้ A เป็นเซตใดๆ

พาวเวอร์เซต คือ เซตของสับเซตทั้งหมดของA เพาเวอร์เซตของA เขียนแทนด้วย P(A) อ่านแล้วอาจจะงงๆ เราลองมาดูตัวอย่างเพื่อให้เข้าใจง่ายขึ้น

เช่น

1.) A = {1,2} สับเซตของเซต A ประกอบด้วย Ø, {1}, {2}, {1,2} จะเห็นว่าจำนวนสับเซตของเซต A = 4 = 2²

ดังนั้น เพาเวอร์เซตของเซต A คือ P(A) = {Ø, {1}, {2}, {1,2}}

2.) A = {1,2,3} จะได้ว่า P(B) = {Ø, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}} จำนวนสมาชิกของ P(B) = 8 = 2³

เราจะสังเกตเห็นว่า เซต A มีจำนวนสมาชิกเท่ากับ 2 จำนวนสมาชิกของ P(A) = 2²

เซต B มีจำนวนสมาชิกเท่ากับ 3 จำนวนสมาชิกของ P(B) = 2³

สรุป เพาว์เวอร์เซต ( power set )

ถ้า A เป็นเพาว์เวอร์เซต (Power Set) ของเซต A คือ เซตที่มีสมาชิกประกอบไปด้วยสับเซตของ A ทั้งหมด

เพาเวอร์เซตของ A เขียนแทนด้วย P(A) = {สับเซตทั้งหมดของA}

เช่น ถ้า A={1,2} สับเซตของ A คือ ∅,{1},{2},{1,2}หรือ A

ดังนั้น P(A)={∅,{1},{2},A}

คุณสมบัติของเพาว์เวอร์เซต

กำหนดให้ A และ B เป็นเซตใดๆ

1. ∅∈P(A) เพราะ ∅⊂A เสมอ

2. ∅⊂P(A) เพราะเซตว่างเป็นสับเซตของทุกเซต แล้ว P(A) ก็เป็นเซตเช่นกัน

3. A∈P(A) เพราะ A⊂Aเสมอ

4. ถ้า A เป็นเซตจำกัด และ n(A) คือจำนวนสมาชิกของ A แล้วP(A)จะมีสมาชิก2n(A) ตัว (เท่ากับจำนวนสับเซตของ A)

5. A⊂B ก็ต่อเมื่อ P(A)⊂P(B)

6. P(A)∩P(B)=P(A∩B)

กฎทางพืชคณิตของเซต (Laws of the Algebra of Sets) ให้ A, B, C เป็นเซตใด ๆ

กฎทางพืชคณิตของเซต

Union

Intersection

1. Idempotent Laws

2. กฎการเปลี่ยนกลุ่มได้ (Associative Laws)

3. กฎการสลับที่ (Commutative Laws)

4. กฎการกระจาย (Distributive Laws)

5. กฎเอกลักษณ์ (Identity Laws)

6. Complement Laws

7. De Morgan’s Laws

A ∪ A = A

A ∪ ∅ = A

A ∪ U = U

(A ∪ B) ∪ C = A ∪ (B ∪ C)

A ∪ B = B ∪ A

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

A ∪ ∅ = A

A ∪ A’ = U

(A ∪ B)’ = A’ ∩ B’

A ∩ A = A

A ∩ ∅ =∅

A ∩ U = A

(A ∩ B) ∩ C = A ∩ (B ∩ C)

A ∩ B = B ∩ A

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

A ∩ U = A

A ∩ A’ = ∅

(A ∩ B)’ = A’ ∪ B’

การหาจำนวนสมาชิกของเซต
กำหนดให้ เป็นเอกภพสัมพัทธ์ A, B และ C เป็นเซตจำกัด ซึ่งต่างก็เป็นสับเซตของเอกภพสัมพัทธ์
1. ถ้า A และ B เป็นเซตจำกัด และ A ∩ B = ∅ แล้ว n(A ∪ B) = n(A)+n(B)
2. ถ้า A และ B เป็นเซตจำกัดใด ๆ และ A ∩ B ≠ ∅ แล้ว n(A ∪ B) = n(A)+n(B)-n(A ∩ B)