เวกเตอร์ คณิตศาสตร์ ม.ปลาย
กำหนดเส้นตรง XX’ , YY’ และ ZZ’ เป็นเส้นตรงที่ผ่านจุด O และตั้งฉากซึ่งกันและกันโดยกำหนด ทิศทางของเส้นตรงทั้งสามเป็นระบบมือขวา ดังรูป
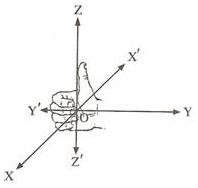
ถ้าเส้นตรงทั้งสามเป็นเส้นจำนวน (real line) จะเรียกเส้นตรง XX’ , YY’ และ ZZ’ ว่า
แกนพิกัด X แกนพิกัด Y และ แกนพิกัด Z หรือเรียนสั้นๆ ว่า แกน X (x-axis) แกน Y (y-axis) และ แกน Z (z-axis) และเรียนจุด O ว่า จุดกำเนิด (origin) ดังรูป
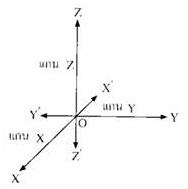
เรียกส่วนของเส้นตรง OX OY และ OZ ว่า แกน X ทางบวก (positive x-axis) แกน Y ทางบวก (positive y-axis) และ แกน Z ทางบวก (positive z-axis) และเรียกส่วนของเส้นตรง OX’ OY’ และ OZ’ ว่า แกน X ทางลบ (negative x-axis) แกน Y ทางลบ (negative y-axis) และ แกน Z ทางลบ (negative z-axis)
ความหมายของเวกเตอร์
ในการกล่าวถึงปริมาณใดๆ เราจำแนกปริมาณออกเป็น 2 ประเภท ได้แก่
ปริมาณสเกลาร์ ( Scalar Quantity ) คือ ปริมาณที่บอกเพียงขนาดอย่างเดียว เช่น ระยะทาง อัตราเร็ว อัตราเร่ง
ปริมาณเวกเตอร์ (Vector Quantity ) คือ ปริมาณที่บอกทั้งขนาดและทิศทาง เช่น การกระจัด ความเร็ว ความเร่ง
สัญลักษณ์ที่ใช้แทนปริมาณเวกเตอร์
เวกเตอร์ที่จะกล่าวในระดับนี้เป็นเวกเตอร์ในระนาบเท่านั้น
ปริมาณเวกเตอร์ สามารถเขียนแทนด้วย ”ส่วนของเส้นตรงที่ระบุทิศทาง”
โดย ขนาดเวกเตอร์ แทนด้วย ความยาวเส้นตรง
ทิศทางเวกเตอร์ แทนด้วย หัวลูกศร
ใช้สัญลักษณ์ AB แทนส่วนของเส้นตรงที่ระบุทิศจาก A ไป B อ่านว่า เวกเตอร์เอบี เรียก A ว่าจุดเริ่มต้น (initial point) ของ
AB เรียก B ว่าจุดสิ้นสุด(terminal point) ของAB หัวลูกศรจะอยู่ที่จุดสื้นสุด
ขนาดของเวกเตอร์AB คือความยาวของส่วนของเส้นตรง AB ใช้สัญลักษณ์ |AB| ขนาดนี้จะเป็นปริมาณสเกลาร์
อาจใช้สัญลักษณ์ u แทนเวกเตอร์ได้
การเท่ากันของเวกเตอร์
เวกเตอร์ 2 เวกเตอร์จะเท่ากันก็ต่อเมื่อ
1. มีขนาดเท่ากัน 2. มีทิศทางเดียวกัน
นิเสธของเวกเตอร์
นิเสธของเวกเตอร์ คือ เวกเตอร์ที่มีขาดเท่ากันแต่ทิศทางตรงกันข้าม
ให้ u เป็นเวกเตอร์ใดๆ เขียนแทนนิเสธของ u ด้วย – u
เวกเตอร์ศูนย์
เวกเตอร์ศูนย์ คือ เวกเตอร์ที่มีจุดเริ่มต้นและจุดสิ้นสุดเป็นจุดเดียวกัน
ดังนั้น เวกเตอร์ศูนย์คือจุดนั่นเอง เนื่องจากไม่มีความยาว และมีขนาดเท่ากับศูนย์
การบวกและลบเวกเตอร์
กรณีที่เป็นการบวกเวกเตอร์
นิยาม ให้ u และ v เป็นเวกเตอร์ 2 เวกเตอร์ใดๆในระนาบ สามารถหา u+v ได้โดยเลือกจุด A
จุดใดจุดหนึ่งมาหาจุด B ที่ทำให้ u = AB และหาจุด C ที่ทำให้ v = BC ซึ่งจะได้ w = AC จะได้
AC = AB + BC หรือ w = u + v
ในกรณีที่เป็นการลบเวกเตอร์
ให้ u และ v เป็นเวกเตอร์ใดๆในระนาบ ลบของเวกเตอร์ u ด้วย v เขียนแทนได้ด้วย u – v และ
u – v = u + ( -v )
วกเตอร์ (Vector) ในระบบพิกัดฉาก(2มิติ)และ 3 มิติ
เวกเตอร์ในระบบพิกัดฉาก 2 มิติและ 3 มิติ
เนื้อหาประกอบด้วย
2.1 ระบบพิกัด
2.2 เวกเตอร์
2.3 ส่วนประกอบของเวกเตอร์
2.4 การบวกเวกเตอร์
2.5 เวกเตอร์ตำแหน่ง
2.6 การคูณเวกเตอร์

เวกเตอร์เป็นเครื่องมือทางคณิตศาสตร์อย่างหนึ่ง ซึ่งดูเหมือนไม่มีความจำเป็นแตเป็นเครื่องมืออย่างแรกที่ต้องใช้ อย่างไรก็ตามในการศึกษาทางฟิสิกส์เวกเตอร์เป็นเครื่องมือที่มีความสำคัญ เพื่อช่วยในอำนวยความสะดวกในการคำนวณ
2.1 ระบบพิกัด (แกนอ้างอิง)
ระบบพิกัดมีความสำคัญเพื่อช่วยในการวัดมีความหมาย เช่นอีก 800 m ถึงอาคารวิทยาศาสตร์เป็นการบอกที่ไม่สมบูรณ์ เนื่องจากไม่ทราบว่าเริ่มต้นที่ตำแหน่งใด
ดังนั้นในการกำหนดระบบพิกัดต้องทราบ
ก. จุดเริ่มต้น
ข. ชนิดของระบบพิกัด (พิกัดฉาก ; พิกัดเชิงขั้ว ; พิกัดทรงกระบอก)
ค. ทิศตามแกน
ระบบพิกัดแบบมาตรฐานใน 2 มิติ
ได้แก่ระบบพิกัดฉาก (Cartesian) และ ระบบพิกัดเชิงขั้ว (Polar)
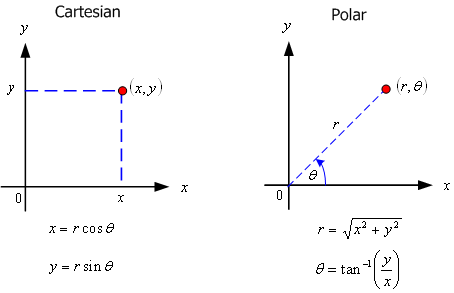
ระบบพิกัดแบบมาตรฐานใน 3 มิติ
ได้แก่ระบบพิกัดฉาก (Cartesian) และ ระบบพิกัดทรงกระบอก (Cylindrical) และระบบพิกัดทรงกลม (Spherical)
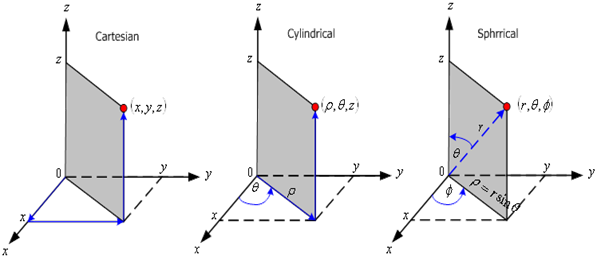
รูปที่ 2.3 ระบบพิกัดฉากใน 3 มิติ
2.2 เวกเตอร์
สเกลาร์ : ปริมาณที่มีเฉพาะขนาดอย่างเดียว
เวกเตอร์ : ปริมาณที่มีทั้งขนาดและทิศทาง
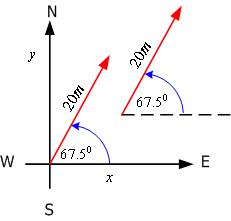
รูปที่ 2.1 แสดงระบบพิกัดใน 2 มิติ
สัญลักษณ์ที่ใช้
(รูปที่ 1)
บทนิยาม 1 ถ้าเวกเตอร์ u และ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ แล้ว ผลบวกของเวกเตอร์ u และ v เขียนแทนด้วยเวกเตอร์ u + v หาได้จากให้ตำแหน่งเวกเตอร์ v มีจุดเริ่มต้นอยู่ที่จุดสิ้นสุดของเวกเตอร์ u
เวกเตอร์ u + v จะแทนด้วยลูกศรจากจุดเริ่มต้นของเวกเตอร์ u ไปยังจุดสิ้นสุดของเวกเตอร์ v ดังรูปที่ 2
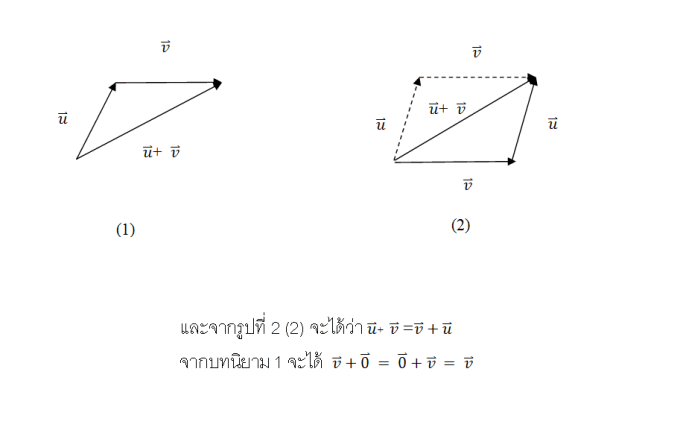 (รูปที่ 2)
(รูปที่ 2)
บทนิยาม 2 ให้เวกเตอร์ v เป็นเวกเตอร์ที่ไม่ใช่เวกเตอร์ศูนย์ และ k เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ แล้ว เวกเตอร์ kv หมายถึงเวกเตอร์ที่มีขนาดเท่ากับ |k| เท่าของเวกเตอร์ v เมื่อ k>0เวกเตอร์ kv จะมีทิศทางเดียวกับ v และเมื่อ k<0 เวกเตอร์ kvมีทิศตรงข้ามกับเวกเตอร์ v และให้เวกเตอร์ kv =0 เมื่อ k =0
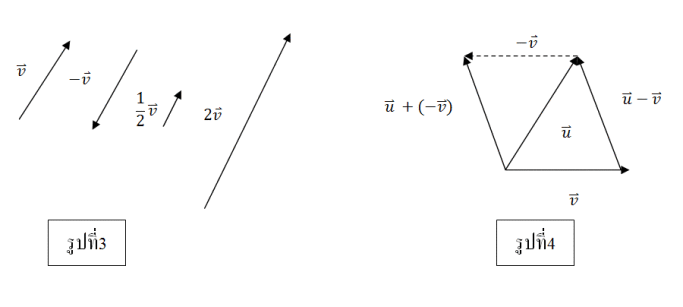
จากรูปที่ 3 ได้ว่าเวกเตอร์ v กับเวกเตอร์ Kv เป็นเวกเตอร์ที่ขนานกัน
เวกเตอร์ตำแหน่ง (Position Vector)
เวกเตอร์ตำแหน่ง หมายถึง เวกเตอร์ที่บอกตำแหน่งของวัตถุเทียบกับจุดใดจุดหนึ่ง เรียกว่า จุดอ้างอิง
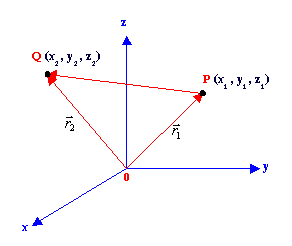
จากรูปเวกเตอร์ ![]() และ
และ ![]() เป็นเวกเตอร์บอกตำแหน่งของจุด P และ Q เทียบกับจุด O ในระบบพิกัด โดย
เป็นเวกเตอร์บอกตำแหน่งของจุด P และ Q เทียบกับจุด O ในระบบพิกัด โดย
![]()
![]()
จะได้
![]()
![]()
โดยขนาดของ ![]() คือ
คือ
![]() ……………………………….(11)
……………………………….(11)
ทิศทางของ ![]() หาได้จาก
หาได้จาก


 …… (12)
…… (12)






