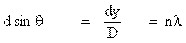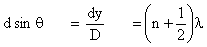สรุป เนื้อหา ฟิสิกส์ ม.5 เทอม 1 และ ฟิสิกส์ ม.5 เทอม 2
ฟิสิกส์ ม.5 เทอม 1
- การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
- คลื่น
- แสงเชิงคลื่นและแสงเชิงรังสี
ฟิสิกส์ ม.5 เทอม 2
- เสียง
- ไฟฟ้าสถิต
- ไฟฟ้ากระแส
การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
การเคลื่อนที่แบบฮาร์โมนิกอย่างง่าย
การเคลื่อนที่แบบฮาร์โมนิกอย่างง่าย (Simple Harmonic Motion : SHM) คือ การเคลื่อนที่กลับไปมาซ้ำทางเดิมโดยผ่านตำแหน่งสมดุล และมีคาบของการเคลื่อนที่คงตัว เช่น การเคลื่อนที่ของวัตถุติดปลายสปริง การสั่นของสายเครื่องดนตรี การแกว่งของลูกตุ้มนาฬิกา เป็นต้น
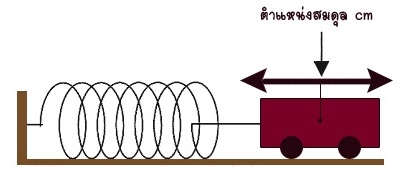
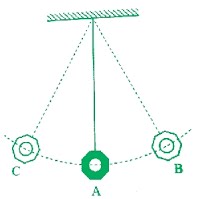
ปริมาณที่สำคัญในการเคลื่อนที่แบบฮาร์โมนิกอย่างง่าย คือ
1.ความถี่ (f) คือ จำหน่วยรอบของการเคลื่อนที่ใน 1 วินาที หน่วยเป็น เฮิรตซ์
2.การขจัด คือระยะทางที่วัตถุเคลื่อนที่ไปโดยนับจากจุดสมดุล
3.คาบ (T) คือ เวลาในการเคลื่อนที่ครบ 1 รอบ หน่วยเป็นวินาที (s)
4.แอมพลิจูด ตือ ระยะทางมากที่สุดที่วัตถุจะสามารถเคลื่อนที่ไปได้ โดยนับจากจุดสมดุลเช่นเดียวกัน อาจพิจารฯาได้ว่า แอมพลิจูดคือการขจัดที่มีปริมาณมากที่สุด
ความถี่และคาบมีความสัมพันธ์ตามสมการ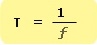
การกระจัด X ในรูปฟังก์ชันของเวลา t ของ SHM เขียนได้เป็น
ซึ่ง

เป็นการกระจัดสูงสุดหรือแอมพิจูด

เป็นความถึ่เชิงมุมมีค่าเท่ากับ

หรือ

 เป็นค่าคงตัวทางเฟสหมายถึงเฟสเริ่มต้น
เป็นค่าคงตัวทางเฟสหมายถึงเฟสเริ่มต้น
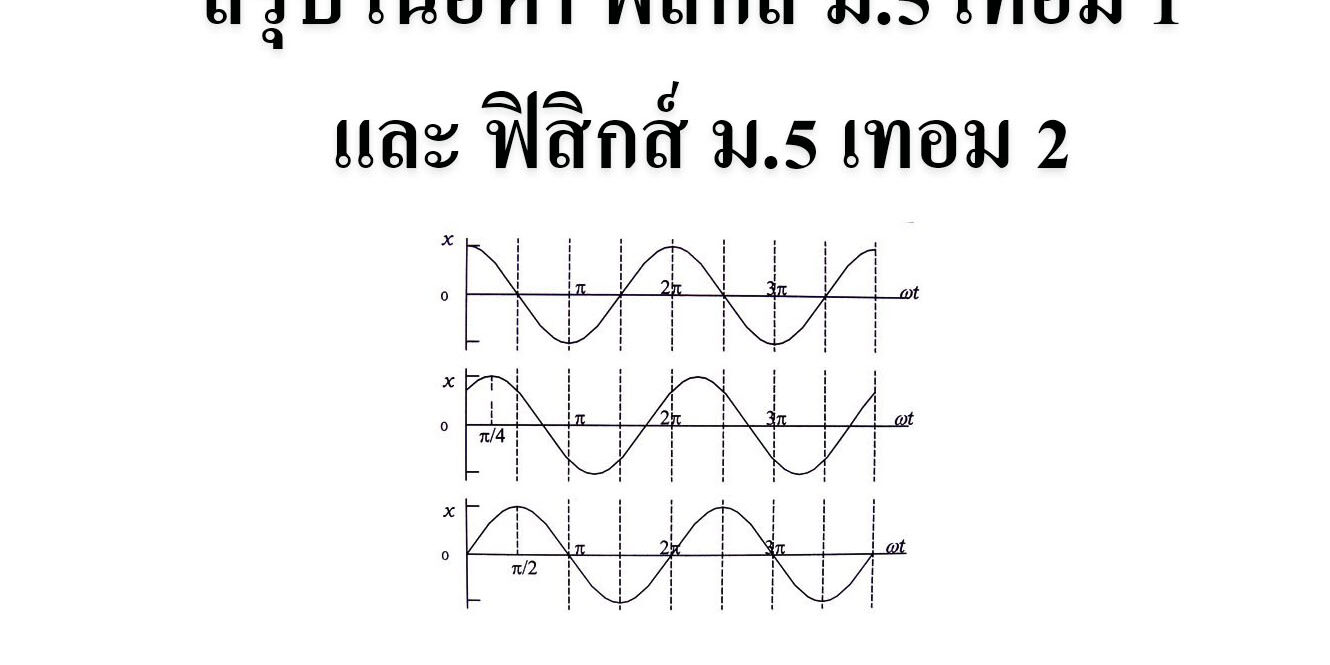
จากรูป หากอนุภาคเริ่มเคลื่อนที่จากตำแหน่งสมดุล (x = 0) ซึ่งมีลักษณะเช่นเดียวกับกราฟของ
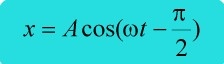
จะได้สมการเคลื่อนที่แบบฮาร์โมนิกอย่างง่าย รูปที่วไปเป็น
เมื่อ a คือ แอมพลิจูด
ลักษณะสำคัญประการหนึ่งของการเคลื่อนที่าแบบฮาร์โมนิกอย่างง่าย คือ
การมีความเร่งแปรผันตรงกับการกระจัด แต่มีทิศทางตรงกันขจ้าม โดยทิศของความเร่งจะเป็นทิศเดียวกับแรง และแรงจะต้องเป็นแรงเข้าหาจุดสมดูลใน
ขณะที่การขัจดมีทิศออกไปจากจุดสมดุลดังสมการ
ความเร่งของการเคลือ่นที่แบบฮาร์โมนิก

คลื่น (wave) เป็นปรากฏการณ์ที่แสดงการถ่ายโอนพลังงานออกจากแหล่งกำเนิด ขณะที่มีการเกิดคลื่น คลื่นมีการเคลื่อนที่รูปแบบหนึ่งในลักษณะเฉพาะ คลื่นมีหลายแบบ เช่น คลื่นกล คลื่นตามขวาง คลื่นตามยาว คลื่นแม่เหล็กไฟฟ้า องค์ประกอบหลักของคลื่นได้แก่ สันคลื่น ยอดคลื่น ท้องคลื่น การกระจัด แอมพลิจูด ความยาว คาบ ความถี่
คลื่น
การจำแนกคลื่น สามารถจำแนกได้หลายวิธี
1. จำแนกคลื่นตามความจำเป็นของการใช้ตัวกลางในการแผ่ สามารถแบ่งคลื่นออกได้ 2 ชนิด คือ
1.1) คลื่นกล (mechanical wave) เป็นคลื่นที่เกิดจากการสั่นของแหล่งกำเนิดคลื่น ต้องอาศัยตัวกลางในการเคลื่อนที่ โดยอนุภาคของตัวกลางสั่นอยู่กับที่ เช่น คลื่นน้ำ คลื่นเสียง คลื่นในเส้นเชือก
1.2) คลื่นแม่เหล็กไฟฟ้า (electromagnetic waves) เป็นคลื่นที่เกิดจากการเหนี่ยวนำให้เกิดการเปลี่ยนแปลงของสนามแม่เหล็กและสนามไฟฟ้า ในทิศทางตั้งฉากซึ่งกันและกัน และต่างก็ตั้งฉากกับทิศทางการแผ่ของคลื่น คลื่นแม่เหล็กไฟฟ้าสามารถแผ่ไปได้ในบริเวณสุญญากาศ ซึ่งไม่มีตัวกลางอยู่เลย หรือแผ่ผ่านบริเวณที่มีตัวกลางต่างๆ ก็ได้ คลื่นประเภทนี้ เช่น คลื่นวิทยุ เรดาร์ ไมโครเวฟ แสง รังสีอัตราไวโอเลต รังสีเอ็กซ์ เป็นต้น
2. จำแนกคลื่นตามลักษณะการสั่นของแหล่งกำเนิด หรือตามลักษณะการแผ่ แบ่งออกได้ 2 ชนิดคือ
คลื่น (wave) เป็นปรากฏการณ์ที่แสดงการถ่ายโอนพลังงานออกจากแหล่งกำเนิด ขณะที่มีการเกิดคลื่น คลื่นมีการเคลื่อนที่รูปแบบหนึ่งในลักษณะเฉพาะ คลื่นมีหลายแบบ เช่น คลื่นกล คลื่นตามขวาง คลื่นตามยาว คลื่นแม่เหล็กไฟฟ้า องค์ประกอบหลักของคลื่นได้แก่ สันคลื่น ยอดคลื่น ท้องคลื่น การกระจัด แอมพลิจูด ความยาว คาบ ความถี่
การจำแนกคลื่น สามารถจำแนกได้หลายวิธี
1. จำแนกคลื่นตามความจำเป็นของการใช้ตัวกลางในการแผ่ สามารถแบ่งคลื่นออกได้ 2 ชนิด คือ
1.1) คลื่นกล (mechanical wave) เป็นคลื่นที่เกิดจากการสั่นของแหล่งกำเนิดคลื่น ต้องอาศัยตัวกลางในการเคลื่อนที่ โดยอนุภาคของตัวกลางสั่นอยู่กับที่ เช่น คลื่นน้ำ คลื่นเสียง คลื่นในเส้นเชือก
1.2) คลื่นแม่เหล็กไฟฟ้า (electromagnetic waves) เป็นคลื่นที่เกิดจากการเหนี่ยวนำให้เกิดการเปลี่ยนแปลงของสนามแม่เหล็กและสนามไฟฟ้า ในทิศทางตั้งฉากซึ่งกันและกัน และต่างก็ตั้งฉากกับทิศทางการแผ่ของคลื่น คลื่นแม่เหล็กไฟฟ้าสามารถแผ่ไปได้ในบริเวณสุญญากาศ ซึ่งไม่มีตัวกลางอยู่เลย หรือแผ่ผ่านบริเวณที่มีตัวกลางต่างๆ ก็ได้ คลื่นประเภทนี้ เช่น คลื่นวิทยุ เรดาร์ ไมโครเวฟ แสง รังสีอัตราไวโอเลต รังสีเอ็กซ์ เป็นต้น
2. จำแนกคลื่นตามลักษณะการสั่นของแหล่งกำเนิด หรือตามลักษณะการแผ่
แสงเชิงคลื่นและแสงเชิงรังสี
การแทรกสอดของแสง (Interference)
การ แทรกสอดของแสง (Interference) เกิดได้ต่อเมื่อคลื่นแสง 2 ขบวนเคลื่อนที่มาพบกัน จะเกิดการรวมตัวกันและแทรกสอดกันเกิดเป็นแถบมืดและแถบสว่างบนฉาก โดยแหล่งกำเนิดแสงจะต้องเป็นแหล่งกำเนิดอาพันธ์ (Coherent Source) คือเป็นแหล่งกำเนิดที่ให้คลื่นแสงความถี่เดียวกัน และความยาวคลื่นเท่ากัน นักวิทยาศาสตร์ที่ประสบความสำเร็จในการทดลองเพื่อทดสอบทฤษฎี คือ โทมัส ยัง นักวิทยาศาสตร์ชาวอังกฤษ
โทมัส ยัง (Thomas Young – 14 มิถุนายน พ.ศ. 2316 – 10 พฤษภาคม พ.ศ. 2372) เป็นนักวิทยาศาสตร์และแพทย์ ชาวอังกฤษ
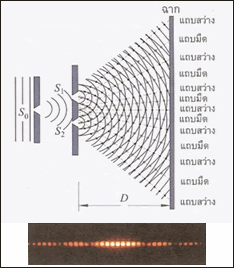
การทดลองเรื่องการแทรกสอดของแสง ทำได้โดย ให้แสงผ่านช่องแคบ (Slit) So แล้วเลี้ยวเบนตกกระทบช่องแคบคู่ S1 , S2 ซึ่งทำหน้าที่เป็นเสมือนแหล่งกำเนิดอาพันธ์ เมื่อแสงเคลื่อนที่ผ่าน S1 , S2 เดินทางไปพบกัน จะทำให้เกิดการแทรกสอดกันในลักษณะทั้งเสริมและหักล้างกัน โดยปรากฎภาพการแทรกสอดบนฉากเห็นเป็นแถบสว่างแถบมืด ดังรูป
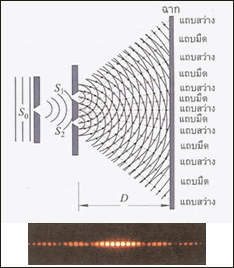
สมการการแทรกสอดของแสง
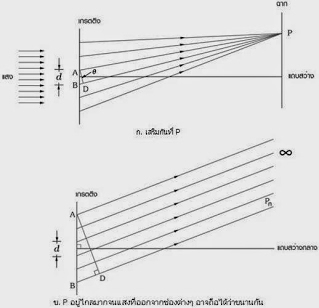
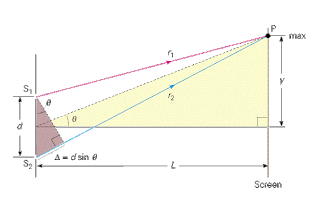
ถ้าให้ ช่องแคบ S1และ S2เป็นแหล่งกำเนิดแสงห่างกันเป็นระยะ d เมื่อแสงเดินทางจากช่องแคบมาถึงฉากด้วยระยะทางที่ต่างกัน เดินทางมาพบกันบนจุดเดียวกันคือจุด P จะได้ผลต่าง S1P กับ S2P เป็นดังสมการ
จากภาพการแทรกสอดของแสง พบว่า
S2P – S1P = d sinθ
เนื่องจากมุม เป็นมุมน้อย ๆ จะได้ = สามารถสรุปสมการที่ใช้คำนวณเกี่ยวกับสลิตคู่ ดังนี้
1. เมื่อ S1 , S2มีเฟสตรงกัน
การแทรกสอดแบบเสริมกัน(แนวกลางเป็นแนวปฏิบัพ A0)
S2P – S1P = nλ
d sinθ = nλ
d y/L = nλ
เมื่อ n = 0, 1, 2, 3, ….
การแทรกสอดแบบหักล้างกัน
S2P – S1P = (n-1/2)λ
d sinθ = (n-1/2)λ
d y/L = (n-1/2)λ
เมื่อ n = 1, 2, 3, ….
2. เมื่อ S1 , S2มีเฟสตรงข้ามกัน
การแทรกสอดแบบเสริมกัน
S2P – S1P = (n-1/2)λ
d sinθ = (n-1/2)λ
d y/L = (n-1/2)λ
เมื่อ n = 1, 2, 3, ….
การแทรกสอดแบบหักล้างกัน (แนวกลางเป็นแนวบัพ N0)
S2P – S1P = nλ
d sinθ = nλ
d y/L = nλ
เมื่อ n = 0, 1, 2, 3, ….
การเลี้ยวเบนของแสง (Diffraction)
ถ้าเราวางวัตถุทึบแสงไว้ระหว่างฉากกับจุดกำเนิดแสงที่สว่างมากเราจหะเห็นขอบของเงาวัตถุนั้นบนฉากพร่ามัว เป็นแถบมืดแถบสว่าง
สลับกันดังรูปที่ 46 ที่เป็นเช่นนี้ เพราะแสงเกิดการเลี้ยวเบนทำให้เกิดการเลี้ยวเบนทำให้เกิดการแทรกสอดเป็นแถบมืดและแถบสว่าง
รูปที่ 46 การเลี้ยวเบนของแสงผ่านวัตถุรูปดาว
จากรูป 46 ถ้าให้แสงที่มีความสว่างมากผ่านวัตถุรูปดาวจะทำให้ เกิดแถบมืดและแถบสว่างที่ขอบในและขอบนอกของรูปดาวปรากฏบนฉาก เพราะคลื่นแสงที่เลี้ยวเบนจากขอบในและขอบนอกของรูปดาวเป็นเสมือนแหล่งกำเนิดแสงใหม่จึงเกิดการแทรกสอดกันเองทำให้เกิดแถบสว่างและแถบมืดทั้งขอบนอกและขอบในของวัตถุรูปดาว
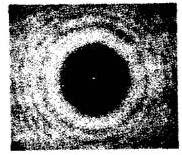
รูปที่ 47 เงาของลูกทรงกลมดันเส้นผ่านศูนย์กลางนิ้ว
จากรูป 47 แสดงการเลี้ยวเบนของแสงโดยให้แสงที่มีความสว่างมากผ่านทรงกลมตัน ทำให้เกิดเงาของทรงกลมปรากฏบนฉาก และเกิดแถบมืดแถบสว่างที่ขอบเนื่องจากการเลี้ยวเบนของแสงที่จุดศูนย์กลางของเงาทรงกลมจะเป็นจุดสว่าง เพราะแสงที่เลี้ยวเบนผ่านขอบของทรงกลมตันจะเป็นเสมือนแหล่งกำเนิดใหม่ตามหลักการของฮอยเกนส์จึงให้คลื่นแสงไปพบกัน ที่จุดศูนย์กลางของเงาทรงกลมบนฉากทำให้เกิดการแทรกสอดกันในลักษณะเสริมจึงเห็นเป็นจุดสว่างขึ้น
การเลี้ยวเบนของแสงผ่านช่องเดี่ยว
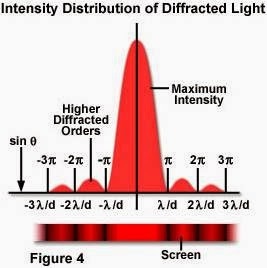
เมื่อให้แสงเลี้ยวเบนผ่านช่องแคบเดียวจะได้แถบสว่างตรงกลางกว้างและมีความเข้มมากที่สุด แถบสว่างข้างๆ ที่สลับแถบมืดจะมีความเข้มลดลง
ถ้าแสงที่ผ่านช่องแคบเป็นแสงสีขาวจะได้แถบสว่างเป็นสีขาวและแถบสว่างข้างๆ จะเป็นสเปคตรัมโดยเรียงจากมีม่วงไปจนถึง สีแดงแต่ถ้าเป็นแสงสีเดียวแถบสีสว่างข้างๆจะเป็นสีเดิม แถบสว่างตรงกลางจะกว้างมากที่สุดและแถบสว่างข้างๆ จะลดลงครึ่งหนึ่งและมีขนาดกว้างเกือบเท่ากันหมด
รูปที่ 48 การเลี้ยวเบนของแสงผ่านช่องเดี่ยว
การหาตำแหน่งแถบมืดแถบสว่างบนฉาก
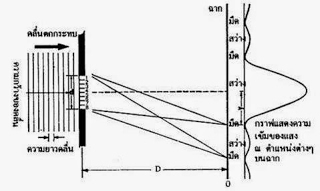
ให้คลื่นแสงสีเดียวความยาวคลื่น ส่องผ่านช่องเดียวที่มีความกว้าง d ทำให้เกิดแทรกสอด เนื่องจากการเลี้ยวเบนบนฉากที่ห่าง จากช่องเดียว D ดังรูปที่ 49
จากรูปที่ 49 อาศัยหลักของฮอยเกนส์ ซึ่งกล่าวว่าทุกจุดบนหน้าคลื่นจะกระทำตัวเป็นแหล่งกำเนิดคลื่นใหม่ ถ้าเราให้ฉากอยู่ห่างจาก ช่องเดี่ยวมากๆ จะได้รังสีที่ออกจากช่องเดียวเป็นรังสีขนาน และตำแหน่งมืดบนฉากคือตำแหน่งที่คลื่นหักล้างกัน
รูปที่ 50 รังสีขนานจากช่องเดียว
พิจารณารูป 50(a) ถ้า เราแบ่งครึ่งช่อง AB เราจะพบว่าถ้ารังสีออกจาก A และ C มีทางเดินต่างกัน λ/2 แล้วทุกๆ คู่ที่อยู่ใต้ A และ B ซึ่งห่างกัน d/2 เช่น D และ E จะมีทางเดินต่างกัน λ/2 ด้วยเป็นผลทำให้คลื่นหักล้างกันหมด บนฉากจะได้ว่าแต่ละคู่มีเงื่อนไขดังนี้
d/2sinθ = λ/2
d/2sinθ = λ เป็นตำแหน่งบัพที่ 1
ทำนองเดียวกันถ้าแบ่งตำแหน่งกว้าง d เป็น 4 ส่วนๆกัน ดังรูป 50(b) จะได้ทุกๆคู่ มีระยะห่างกัน d/4 และจะหักล้างกันเมื่อทางเดินต่างกัน λ/2 นั่นคือ
d/4sinθ = λ/2
dsinθ = λ/2 เป็นตำแหน่งบัพที่ 2
ถ้าแบ่งช่องกว้าง d เป็น 6,8,10,…. จะได้ d/2sinθ = λ/2= 3λ,4 λ,5λ… ตามลำดับ
ฉะนั้นจะได้สูตรการหาสมการหาตำแหน่งบัพ (node) ของการเลี้ยวเบนของแสงสว่างช่องเดียวดังนี้
dsinθ =n/2
 สมการบัพของช่องเดียว
สมการบัพของช่องเดียวเงื่อนไขการเป็นปฏิบัพ (Antinode)
การพิจารณาหาตำแหน่งปฏิบัพโดยตรง ไม่มีการพิจารณา ตำแหน่งปฏิบัพหาได้จากการเฉลี่ยตำแหน่งบัพ
สมการปฏิบัพคือ
 สมการปฏิบัพช่องแคบเดี่ยว
สมการปฏิบัพช่องแคบเดี่ยว
ข้อควรจำ1 . ในการพิจารณาการแทรกสอดของช่องคู่
สมการปฏิบัพ
สมการบัพ
2. ในการพิจารณาการเลี้ยวเบนผ่านช่องแคบเดี่ยวจะได้
สมการปฏิบัพ
สมการบัพ
โดย n เป็นตัวเลขแสดงลำดับที่ของบัพหรือปฏิบัพมีค่าตั้งแต่ 1,2,3, . . .
d = ความกว้างของช่องสลิต (เมตร)
θ= มุมที่เบนไปจากแนวกลาง
n = จำนวนเต็มบวก ( 1, 2, 3, …. )
λ = ความยาวคลื่นแสง (เมตร)
x = ระยะจากกึ่งกลางของแถบสว่างกลางถึง กึ่งกลางของแถบมืดที่ n ใด ๆ
L = ระยะจากช่องเดี่ยวถึงฉาก (เมตร)
เกรตติง (Grating)
เกรตติง คือ อุปกรณ์ ที่ใช้ในการตรวจสอบสเปรคของแสงและหาความยาวคลื่นแสง โดยอาศัย คุณสมบัติการแทรกสอดของคลื่น ลักษณะของเกรตติง จะเป็นแผ่นวัสดุบางที่ถูกแบ่งออกเป็นช่องขนานซึ่งอยู่ชิดกันมาก โดยทั่วไปใน 1 เซนติเมตร แบ่งออกเป็น 10,000 ช่อง ซึ่งจำนวนช่องของเกรตติงอาจมี 100 ถึง 10,000 ช่อง/cm ในการทดลอง ถ้าเราให้แสงจากดวงอาทิตย์หรือแสงขาวจากหลอดไฟส่องผ่านเกรตติง เราจะเห็นสเปรคตรัมของแสงอาทิตย์หรือแสงขาวออกเป็น 7 สี โดยเกรตติงถูกพัฒนามาจากสลิตคู่ด้วยการเพิ่มจำนวนช่วงทั้งสองให้มากขึ้น มีผลทำให้ระยะห่างระหว่างช่องอยู่ใกล้กันมากขึ้นทำให้การเลี้ยวเบนของแสงมาก ขึ้น
ภาพตัวอย่างของแผ่นเกรตติง
แสง ความยาวคลื่นเดียวตกกระทบเกรตติง แสงบางส่วนจะเบนออกจากแนวไปปรากฏบนฉากเป็นแถบสว่างเล็กๆ แถบสว่างนี้เกิดจากการแทรกสอดของแสงจากช่องอื่นๆทุกช่องที่เสมือนเป็นแหล่ง กำเนิดแสงอาพันธ์ การหาตำแหน่งของแถบสว่างให้ถือว่าฉากอยู่ไกลจากเกรตติงมาก จนแสงจากช่องแต่ละช่องของเกรตติงที่เคลื่นที่ไปที่ฉากสามารถประมาณได้ว่า เป็นแสงขนาน
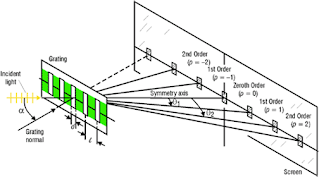
เมื่อ มีแสงความถี่เดียว ความยาวคลื่น λผ่านเกรตติงในแนวตั้งฉากดังรูป จะเกิดการเลี้ยวเบนและแทรกสอดเช่นเดียวกับกรณีสลิตคู่ (ช่องแคบคู่)
ภาพแสดงการเลี้ยวเบนของแสงผ่านเกรตติง
ถ้าเกรตติงมีระยะห่างระหว่างช่องเท่ากับ d ที่ตำแหน่ง P เป็นตำแหน่งบนแถบสว่าง ระยะทางจากช่องแต่ละช่องของเกรตติงถึงจุด P จะไม่เท่ากัน ช่องแต่ละช่องจะเป็นเสมือนแหล่งกำเนิดแสงอาพันธ์ ที่ทำให้คลื่นแสงผ่านออกมามีเฟสตรงกัน การหาตำแหน่งของแถบมืดและแถบสว่างใช้หลักการเดียวกันกับการแทรกสอดของสลิต คู่ จึงได้ว่า
ตำแหน่งแถบสว่างใดๆ (A)
บนฉาก (แนวกลางเป็นแนวปฏิบัพ A
0)
d sinθ = nλ
d x/L = nλ
เมื่อ n = 0, 1, 2, 3, ….
ตำแหน่งแถบมืดใดๆ (N)
บนฉาก
d sinθ = (n-1/2)λ
d x/L = (n-1/2)λ
เมื่อ n = 1, 2, 3, ….
x แทนเป็นระยะจากแถบสว่างตรงกลางถึงจุด P
L แทนระยะห่างจากเกรตติงถึงฉากรับ
λแทนความยาวของคลื่นแสง
d แทนระยะห่างระหว่างช่องของเกรตติง
การหาระยะระหว่างช่องของเกรตติง (d) เราสามารถหาระยะระหว่างช่องของเกรตติง ได้โดยใช้การเทียบอัตราส่วน
เมื่อให้ N แทนจำนวนช่องของเกรตติงใน 1 m.
d แทนระยะห่างระหว่างช่องของเกรตติง
ประโยชน์ของเกรตติง
1. ใช้แยกแสงสีต่างๆ ที่เคลื่อนที่รวมกัน เช่น การหาสเปกตรัมของแสงขาว
2. ใช้หาความยาวคลื่นของแสงสีต่างๆ โดยแสงสีต่างๆ จะมีความยาวคลื่นแตกต่างกัน ทำให้เกิดการเลี้ยวเบนเมื่อผ่านเกรตติงได้แตกต่างกัน โดยแสงสีม่วงเลี้ยวเบนได้น้อยที่สุด ส่วนแสงสีแดงมีความยาวคลื่นมากที่สุดจะเลี้ยวเบนได้มากที่สุด
การกระเจิงของแสง
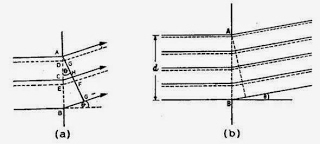
สีของท้องฟ้าเปลี่ยนแปลงไปตามเวลา ตอนกลางวันท้องฟ้าเป็นสีฟ้า ส่วนตอนเช้าและตอนเย็นท้องฟ้าเป็นสีส้มแดง ปรากฏการณ์นี้เกิดขึ้นเพราะ “การกระเจิงของแสง” (Scattering of light) แสงของดวงอาทิตย์ประกอบด้วยแสงสีต่างๆ ซึ่งมีขนาดความยาวคลื่นไม่เท่ากัน เมื่อรังสีจากดวงอาทิตย์ตกกระทบโมเลกุลของอากาศ จะเกิดการกระเจิงของแสง คล้ายกับคลื่นน้ำเคลื่อนที่มากระแทกเขื่อน ดังภาพที่ 1 ถ้าคลื่นมีขนาดเล็กกว่าเขื่อน (λ < d) คลื่นจะกระเจิงหรือสะท้อนกลับ แต่ถ้าคลื่นมีขนาดใหญ่กว่าเขื่อน (λ > d) คลื่นก็จะเคลื่อนที่ข้ามเขื่อนไปได้ ดังภาพที่ 2
ภาพที่ 1 การกระเจิงของแสง
• ปัจจัยที่มีอิทธิพลต่อการกระเจิงของแสง
• ขนาดความยาวคลื่น: แสงสีน้ำเงินมีความยาวคลื่นสั้น แสงสีแดงมีความยาวคลื่นมากกว่า แสงคลื่นสั้นเกิดการกระเจิงได้ดีกว่าแสงคลื่นยาว
ขนาดของสิ่งกีดขวาง: โมเลกุลของแก๊สในบรรยากาศมีขนาดเล็ก ส่วนโมเลกุลของไอน้ำและฝุ่นที่แขวนลอยในบรรยากาศมีขนาดใหญ่ โมเลกุลขนาดใหญ่เป็นสิ่งกีดขวางการเดินทางของแสงความยาวคลื่นสั้น
ภาพที่ 2 คลื่นแสงเคลื่อนที่ผ่านโมเลกุลของกากาศ
• มุมที่แสงตกกระทบกับบรรยากาศ: แสงอาทิตย์เวลาเที่ยงทำมุมชันกับพื้นโลก แสงเดินทางผ่านมวลอากาศเป็นระยะทางสั้น แสงเดินทางผ่านไม่ยาก ส่วนในตอนเช้าและตอนเย็นแสงอาทิตย์ทำมุมลาดกับพื้นโลก แสงเดินทางผ่านมวลอากาศเป็นระยะทางยาว ทำให้แสงเดินทางผ่านได้ยาก
• ปริมาณสารแขวนลอยในอากาศ: ในช่วงเวลาบ่ายและเย็น อากาศและพื้นผิวโลกมีอุณหภูมิสูง มีฝุ่นละอองลอยอยู่ในอากาศมาก เป็นอุปสรรคขวางกั้นทางเดินของแสง


![]()
 เป็นการกระจัดสูงสุดหรือแอมพิจูด
เป็นการกระจัดสูงสุดหรือแอมพิจูด เป็นความถึ่เชิงมุมมีค่าเท่ากับ
เป็นความถึ่เชิงมุมมีค่าเท่ากับ  หรือ
หรือ 
 เป็นค่าคงตัวทางเฟสหมายถึงเฟสเริ่มต้น
เป็นค่าคงตัวทางเฟสหมายถึงเฟสเริ่มต้น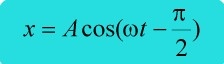
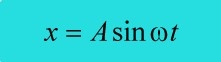

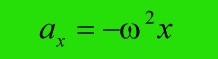


 สมการปฏิบัพช่องแคบเดี่ยว
สมการปฏิบัพช่องแคบเดี่ยว