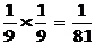กฏเกณฑ์เบื้องต้นเกี่ยวกับการนับ
ในการหาวิธีต่างๆในชีวิตประจำวันนั้น เราจะใช้กฏการนับปกติ โดยกฏการนับนั้นหากไม่ใช้การคำนวณ จะใช้ “เเผนภาพต้นไม้” ในการค้นหา โดยเเผน ภาพต้นไม้นั้นจะมีลักษณะลากยาวไปเรื่อยๆจนถึงขั้นสุดท้ายเเละนับว่ามีกี่วิธี

สามารถนั่งได้ 35 วิธี

สามารถทิ้งได้ทั้งหมด 10 วิธี
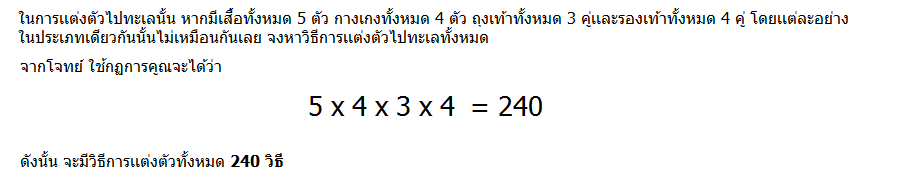


ตัวอย่าง นายดำมีเสื้อ 2 ตัว สีต่างกัน และกางเกง 3 ตัว สีต่างกัน จงหาจำนวนวิธีทั้งหมดที่นายดำสวมเสื้อและกางเกงเป็นชุดต่าง ๆ กัน
วิธีคิด นายดำมีวิธีเลือกสวมเสื้อได้ 2 วิธี
เลือกสวมกางเกงได้ 3 วิธี
ดังนั้น นายดำมีวิธีสวมเสื้อและกางเกงเป็นชุดต่าง ๆ กันได้ (2)(3) = 6 วิธี
อาจใช้แผนภาพต้นไม้ในการหาคำตอบได้ดังนี้
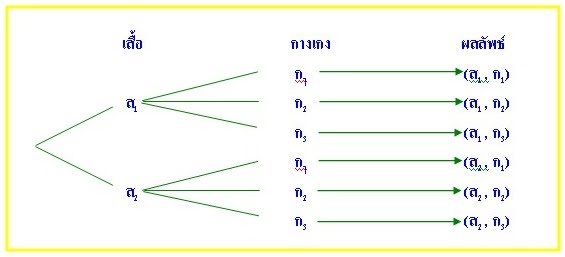
จากแผนภาพต้นไม้ จะได้ว่าจำนวนวิธีทั้งหมดที่นายดำเลือกสวมเสื้อและกางเกงเป็นชุดต่าง ๆ กันเท่ากับ 6 วิธี
หลักการนับ
หลักการบวก
ถ้าการทำงานหนึ่งมีวิธีการทำงาน k วิธี คือ วิธีที่ 1 ถึงวิธีที่ k โดยที่
การทำงานวิธีที่ 1 มีวิธีทำ n1 วิธี
การทำงานวิธีที่ 2 มีวิธีทำ n2 วิธี
: :
การทำงานวิธีที่ k มีวิธีทำ nk วิธี
และวิธีการทำงานแต่ละวิธีแตกต่างกัน แล้วจำนวนวิธีทำงานนี้เท่ากับ n1+n2+…+nk วิธี
ตัวอย่างนักเรียน 3 คนต้องการเข้าและออกห้องห้องหนึ่งซึ่งมีประตู 3 บาน โดยนักเรียนคนที่ 1 เข้าและออกโดยใช้ประตูบานเดียว นักเรียนคนที่ 2 เข้าและออกโดยไม่ใช้ประตูบานเดิม และนักเรียนคนที่ 3 เข้าและออกโดยใช้ประตูบานใดก็ได้ จงหาจำนวนวิธีที่นักเรียนทั้ง 3 คนเข้าและออกห้องนี้
วิธีทำ นักเรียนคนที่ 1 มีวิธีเข้าและออกได้ 3 วิธี
นักเรียนคนที่ 2 มีวิธีเข้าและออกได้ 6 วิธี
นักเรียนคนที่ 3 มีวิธีเข้าและออกได้ 9 วิธี
ดังนั้น วิธีที่นักเรียนทั้ง 3 คนเข้าและออกห้องนี้มีทั้งหมด 3+6+9 = 18 วิธี
หลักการคูณ
ถ้าการทำงานอย่างหนึ่งประกอบด้วยการทำงาน k ขั้นตอน คือ ขั้นตอนที่ 1 ถึงขั้นตอนที่ k ตามลำดับ โดยที่
การทำงานขั้นตอนที่ 1 มีวิธีทำ n1 วิธี
การทำงานขั้นตอนที่ 2 มีวิธีทำ n2 วิธี
การทำงานขั้นตอนที่ 3 มีวิธีทำ n3 วิธี
: :
การทำงานขั้นตอนที่ k มีวิธีทำ nk วิธี
และวิธีการทำงานแต่ละวิธีแตกต่างกัน แล้วจำนวนวิธีการทำงานนี้เท่ากับ n1n2n3…nk วิธี
ตัวอย่าง บริษัทผลิตเสื้อผ้าสำเร็จรูปแห่งหนึ่งผลิตเสื้อ 6 แบบ กางเกง 5 แบบและเนคไท 4 แบบ ถ้าจะจัดแต่งตัวให้กับหุ่นเพื่อนำไปโชว์หน้าร้าน จะสามารถแต่งเป็นชุดต่างๆกันได้กี่ชุด
วิธีทำ ในการแต่งตัวให้กับหุ่นมี 3 ขั้นตอน คือ
ขั้นตอนที่ 1 เลือกเสื้อได้ 6 วิธี
ขั้นตอนที่ 2 เลือกกางเกงได้ 5 วิธี
ขั้นตอนที่ 3 เลือกเนคไทได้ 4 วิธี
ดังนั้น วิธีการแต่งตัวให้กับหุ่นทำได้ทั้งหมด 6×5×4 = 120 วิธี
กฎสำคัญบางประการของความน่าจะเป็น
ให้ A เป็นเหตุการณ์ใดๆ และ S เป็นแซมเปิลสเปซ สมบัติความน่าจะเป็นของ A ดังนี้
1. 0 P (A) 1
2. ถ้า A = { } แล้ว P (A) = 0 นั่นคือ P ( { } ) = 0
3. ถ้า A = S แล้ว P (A) = 1 นั่นคือ P(S) = 1
สมบัติของความน่าจะเป็นของเหตุการณ์ 2 เหตุการณ์
ให้ A และ B เป็นเหตุการณ์ 2 เหตุการณ์ ใน S แซมเปิลสเปซ
1. P (A U B) = P (A) + P (B) – P (A ∩B)
2. P (A U B) = P (A) + P (B) เมื่อ A ∩B = { }
3. P (A) = 1 – P (A’)
4. P (A-B) = P (A) – P (A∩B)
ตัวอย่าง กำหนดให้ P (A) = 0.6 P (B’) = 0.4 และ P (A – B) = 0.2 จงหา P (A ‘∩B’)
จาก P (B’) = 0.4
จะได้ว่า P (B) = 1 – P (B’) = 1 – 0.4 = 0.6
จาก P (A) = 0.6 และ P (A – B) = 0.2
เนื่องจาก P (A) = P (A – B) + P (A ∩B)
(ถ้านักเรียนไม่เข้าใจให้เขียนแผนภาพทางด้านเซตดู)
0.6 = 0.2 + P (A ∩ B)
P (A ∩B) = 0.4
เนื่องจาก P (A’ ∩ B’) = P (A U B)’
= 1 – P (A U B)
จากสมบัติความน่าจะเป็น P (A’ ∩B’) = 1 – [P (A) + P (B) – P (A ∩B)]
= 1 – [0.6 + 0.6 – 0.4] = 1 – 0.8 = 0.2
ความน่าจะเป็นแบบเงื่อนไข
บางครั้งเราทราบว่าเหตุการณ์หนึ่งเกิดขึ้น เราต้องการหาความน่าจะเป็นที่อีกเหตุการณ์หนึ่งเกิดขึ้น เรียกความน่าจะเป็นแบบนี้ว่า ความน่าจะเป็นแบบเงื่อนไข
ให้ A และ B เป็นเหตุการณ์ โดยที่ P (B) > 0 เขียน P (A/B) แทนความน่าจะเป็นของ A เมื่อกำหนดว่าเหตุการณ์ B เกิดขึ้นแล้ว
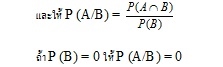
ความน่าจะเป็นของเหตุการณ์ที่เป็นอิสระต่อกัน
พิจารณาในการโยนเหรียญ 1 อัน 2 ครั้ง จะเห็นว่าการที่การโยนเหรียญครั้งหนึ่งขึ้นหัวหรือก้อย ไม่มีผลต่อการขึ้นหัวหรือก้อยในการโยนครั้งที่สอง
เรากล่าวว่าการโยนทั้งสองครั้งเป็นอิสระต่อกัน
นิยาม เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (A ∩B) = P (A) P (B)
ทฤษฎีบท เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (A/B) = P (A)
เหตุการณ์ A และเหตุการณ์ B เป็นอิสระต่อกันก็ต่อเมื่อ P (B/A) = P (B)
ตัวอย่าง โยนลูกเต๋า 2 ลูก 2 ครั้ง จงหาความจะเป็นที่ผลรวมของแต้มแต่ละครั้งเท่ากับ 5
ให้ A แทนเหตุการณ์ที่ผลรวมของแต้มในการโยนครั้งที่ 1 เป็น 5
B แทนเหตุการณ์ที่ผลรวมของแต้มในการโยนครั้งที่ 2 เป็น 5
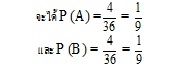
เนื่องจากการโยนลูกเต๋าแต่ละครั้งเป็นอิสระต่อกัน
ดังนั้นความน่าจะเป็นที่ผลรวมของแต้มแต่ละครั้งเป็น 5 เท่ากับ
P (A∩ B) = P (A) P (B)