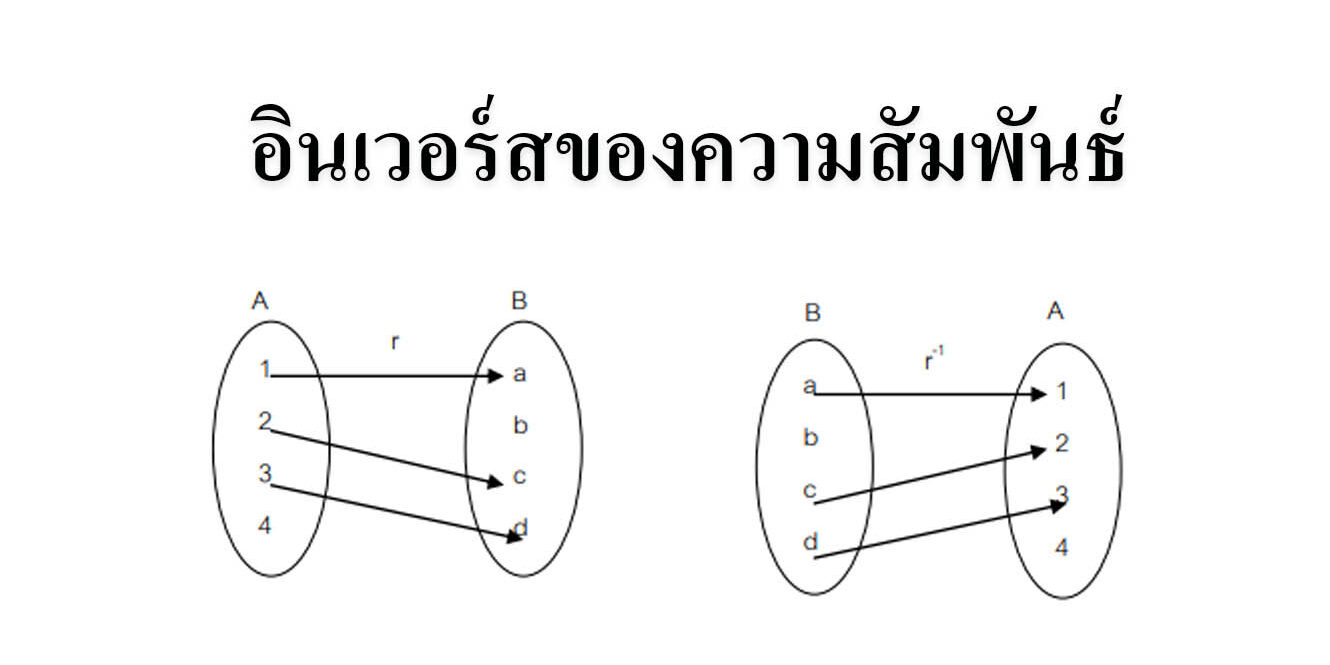
อินเวอร์สของความสัมพันธ์

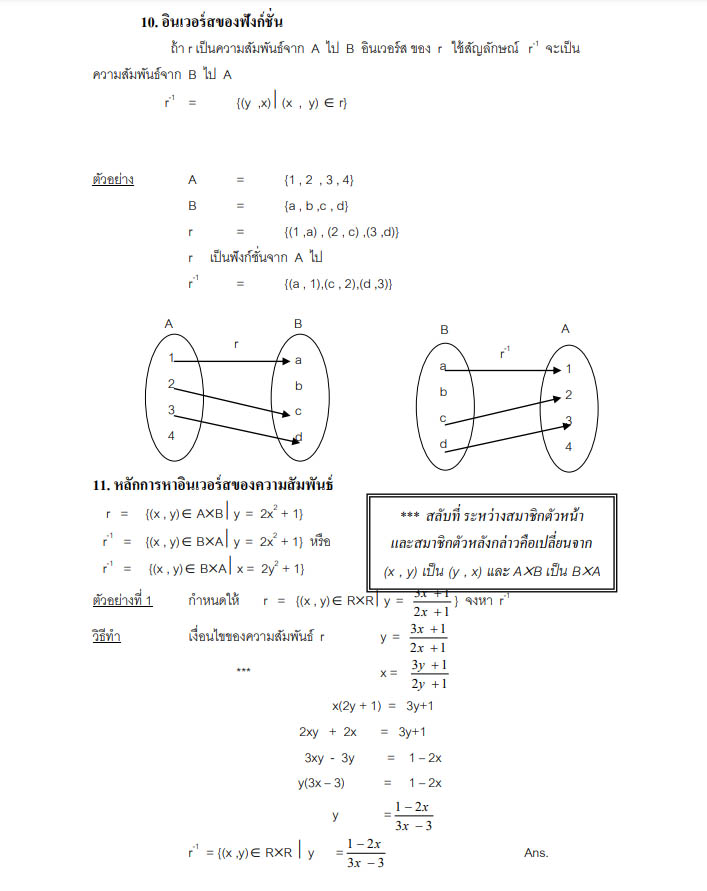
อินเวอร์สของความสัมพันธ์ r คือ ความสัมพันธ์ซึ่งเกิดจากการสลับตำแหน่งของสมาชิกตัวหน้า และสมาชิกตัวหลัง ในแต่ละคู่อันดับที่เป็นสมาชิกของ r เขียนแทนด้วย r^-1

การสลับตำแหน่งของสมาชิกตัวหน้า และสมาชิกตัวหลัง ทำได้ 2 วิธี ดังนี้
	วิธีที่ 1	สลับที่ x และ y ในคู่อันดับ (x, y) แต่มีเงื่อนไขเหมือนเดิม
		ตัวอย่างเช่น	r = {(x, y) ∈ R × R | y = 3x – 1}
		∴	r-1 = {(y, x) ∈ R × R | y = 3x – 1}
	วิธีที่ 2	สลับที่ x และ y ในคู่อันดับ (x, y) โดยแทนที่ x ด้วย y และแทนที่ y ด้วย x แต่ คู่อันดับ (x, y ) เหมือนเดิม
		ตัวอย่างเช่น	r = {(x, y) ∈ R × R | y = 3x – 1}
			r-1 = {(x, y) ∈ R × R | x = 3y – 1}
		∴	r-1 = {(x, y) ∈ R × R | }
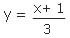สมบัติเกี่ยวกับอินเวอร์สของความสัมพันธ์
	ถ้า r เป็นความสัมพันธ์จากเซต A ไปเซต B
	1. r-1เป็นความสัมพันธ์จากเซต  B ไปเซต A
	2. D r = R r-1 และ R r = D r-1
กราฟของอินเวอร์สของความสัมพันธ์
	เราสามารถวาดกราฟของอินเวอร์สของความสัมพันธ์ได้ 2 วิธีด้วยกัน ดังนี้
	วิธีที่ 1
	1. หาอินเวอร์สของความสัมพันธ์ r-1
	2.วาดกราฟของอินเวอร์สของความสัมพันธ์ โดยใช้เงื่อนไขที่ระบุใน r-1
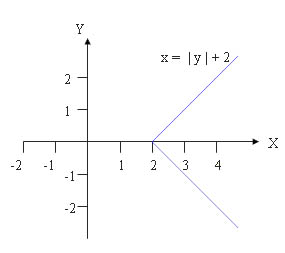
		ตัวอย่างเช่น	r = {(x, y) ∈ R × R | y =  | x | + 2}
		∴	r-1 = {(x, y) ∈ R × R | x =  | y | + 2}
	วิธีที่ 2
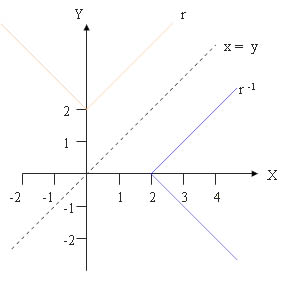
	1.วาดกราฟของความสัมพันธ์ r
	2.กราฟของอินเวอร์สของความสัมพันธ์ คือภาพสะท้อนของกราฟของความสัมพันธ์ r รอบแกน x = y

อินเวอร์สของฟังก์ชั่น