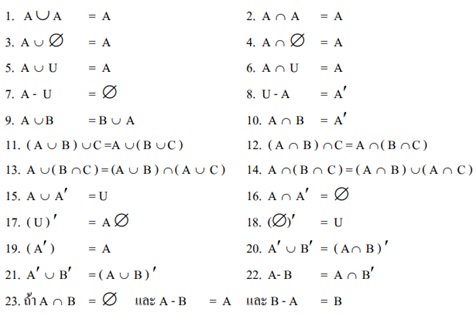เซตคืออะไร? ในทางคณิตศาสตร์

เซตคืออะไร?

เซต คือ คำที่ใช้เรียกกลุ่มของสิ่งต่างๆ

ทำไมต้องเรียนเซต

เซตมีประโยชน์ในเรื่องของการจำแนกสิ่งต่างๆออกเป็นกลุ่มๆ อีกทั้งยังแทรกอยู่ในเนื้อหาบทอื่นๆของคณิตศาสตร์ เราจึงจำเป็นต้องทำความเข้าใจเกี่ยวกับเซต เพื่อที่จะเรียนเนื้อหาบทอื่นๆได้ง่ายขึ้น

ความรู้เบื้องต้นเกี่ยวกับเซต

เซต คือคำที่ใช้เรียกกลุ่มของสิ่งต่างๆ เช่น เซตของสระในภาษาอังกฤษ คือ กลุ่มของสระในภาษาอังกฤษ a,e,i,o,u เป็นต้น

สมาชิกของเซต คือ สิ่งที่อยู่ในเซต เช่น เซตของสระในภาษาอังกฤษ สมาชิกของเซต คือ a,e,i,o,u

การเขียนเซต

การเขียนเซตจะเขียนได้ 2 วิธี

1.) เขียนแบบแจกแจงสมาชิก คือการเขียนสมาชิกไว้ในวงเล็บปีกกา “{ }”แล้วคั่นสมาชิกแต่ละตัวด้วย “,” เช่น

ให้ A แทนเซตของจำนวนนับที่น้อยกว่า 10

ดังนั้น A = {1,2,3,4,5,6,7,8,9}

2.) เขียนแบบบอกเงื่อนไข คือการกำหนดตัวแปรขึ้นมาแล้วใส่เงื่อนไขให้ตัวแปรนั้น เช่น

A = {x|x ∈ N และ x < 10}  จากข้อความนี้ แปลได้ว่า A เท่ากับ x โดยที่ x เป็นสมาชิกของจำนวนนับและ x น้อยกว่า 10

“|” แทนคำว่า โดยที่ หรืออาจจะใช้ “:” แทนคำว่าโดยที่ก็ได้

ประเภทของเซต

1.) เซตว่าง (Empty set) คือเซตที่มีจำนวนสมาชิกเป็น 0 โดยจะใช้สัญลักษณ์ Ø หรือ { } แทน เซตว่าง

เช่น ให้ A แทนเซตของจำนวนเดือนที่มี 32 วัน เราจะเห็นว่าไม่มีเดือนไหนที่มี 32 วัน ดังนั้น A = Ø หรือ A = { }

2.) เซตจำกัด (Finite set) คือ เซตที่สามารถระบุจำนวนสมาชิกได้

เช่น เซตของของจำนวนนับที่น้อยกว่า 10  สามารถเขียนได้ดังนี้ {1,2,3,4,5,6,7,8,9}  จะเห็นว่ามีจำนวนสมาชิกเท่ากับ 9

**เซตว่าง เป็นเซตจำกัด เนื่องจากมีจำนวนสมาชิกเท่ากับ 0**

3.) เซตอนันต์ (infinite set) คือ เซตที่ไม่สามารถระบุจำนวนสมาชิกได้ เช่น

เซตของจำนวนนับ {1,2,3,…} เป็นเซตอนันต์ เพราะเราไม่สามารถบอกได้ว่ามีจำนวนสมาชิกเท่าไหร่

เซตของจำนวนเต็ม {…,-3,-2,-1,0,1,2,3,…} เป็นเซตอนันต์

ชนิดของเซท

• เซตว่าง (Empty Set หรือ Null Set) หมายถึง เซทที่ไม่มีสมาชิกหรืออาจะกล่าวได้ว่าเซตว่างมีสมาชิก 0 สมาชิก โยสัญลักษณ์ที่ใช้ คือ { }
• เซตจำกัด (Finite Set) หมายถึง เซตที่สามารถนับจำนวนสมาชิกได้ครบถ้วน สามารถบอกได้ว่ามีจำนวนสมาชิกเท่าใด เป็นจำนวนเต็มบวกหรือศูนย์
• เซตอนันต์ (Infinite Set) หมายถึง เซตที่มีจำนวนสมาชิกมากมายนับไม่ถ้วน ไม่สามารถบอกได้ว่ามีจำนวนเท่าใด
• เซตเท่ากัน (Equal Set) หมายถึง เมื่อ A และ B เป็นเซตใดๆ A จะเรียกว่าเท่ากับ B ก็ต่อเมื่อเซตทั้งสองมีจำนวนสมาชิกเท่ากันและเหมือนกันทุกสมาชิก ซึ่งจะเขียนแทนด้วยสัญลักษณ์ A – B หรืออาจกล่าวได้ว่าเซตสองเซตใดๆ จะเท่ากันก็ต่อเมื่อสมาชิกของ A ทุกสมาชิกเป็นสมาชิกของ B และสมาชิกทุกสมาชิกของ B เป็นสมาชิกของ A นั่นคือ A = B ก็ต่อเมื่อ ถ้า x ϵ A แล้ว X ϵ B และ ถ้า X ϵ B แล้ว X ϵ A
• เซตเสมอเหมือนกัน (Equivalent Set) คือ เซต 2 เซตใดๆ ที่มีจำนวนสมาชิกเท่ากันแต่ไม่เหมือนกันทุกตัว เรียกว่า เซตเสมอ ฃเหมือน A เสมอเหมือน B จะเขียนแทนด้วย A ≡ B นั่นคือเซต 2 เซตที่เท่ากันเสมอเหมือนกัน แต่เซต 2 เซตที่เสมอเหมือนกันอาจจะเท่ากัน หรือไม่เท่ากันก็ได้
• สับเซต (Sub Set) กำหนด A และ B เป็นเซตใดๆ A จะเรียกเป็นสับเซตของ B ซึ่งเขียนแทนด้วยสัญลักษณ์ A C Bก็ต่อเมื่อ X ϵ A แล้ว X ϵ B
• พาวเวอร์เซท (Power Set) คือ เซตของสับเซตทั้งหมดของเซต A เมื่อ A เป็นเซตจำกัด เพาเวอร์เซตของเซต A เขียนแทนด้วย P(A)

เอกภพสัมพัทธ์และแผนภาพเวนน์-ออยเลอร์

เอกภพสัมพัทธ์ (Relatively Universe) คือ เซตที่กำหนดขึ้น โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่ไม่เป็นสมาชิกของเซตนี้ นิยมใช้สัญลักษณ์ U แทนสัญลักษณ์เอกภพสัมพัทธ์

แผนภาพของเวนน์-ออยเลอร์ (Venn-Euler) คือ แผนภาพที่ใช้เพื่อให้การศึกษาเกี่ยวกับเซตให้เข้าใจง่ายมากยิ่งขึ้น โดยจะแทนเอกภพสัมพัทธ์ด้วยสี่เหลี่ยมมุมฉาก และแทนเซตอื่น ๆ ด้วยวงกลมหรือรูปเรขาคณิตอื่นๆ สมาชิกของเอกกพสัมพันธ์อยู่ภายในรูปสี่เหลี่ยม และสมาชิกของ A อยู่ภายในวงกลม

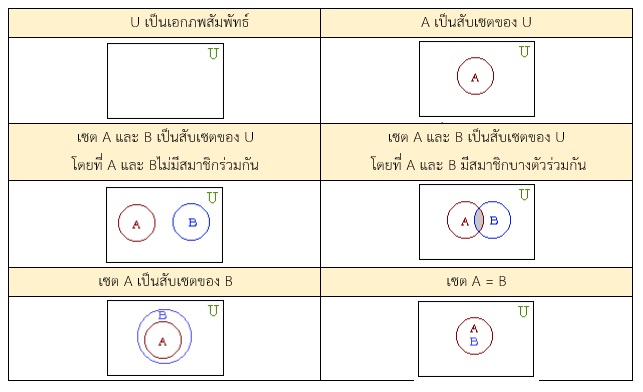
การดำเนินการระหว่างเซต

• ยูเนียน (Union) : ยูเนียนของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A หรือ B เขียนแทนด้วย A ∪ B
• อินเตอร์เซคชัน (Intersection) : อินเตอร์เซคชันของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A และ B เขียนแทนด้วย A ∩ B
• คอมพลีเมนต์ (Complement) : คอมพลีเมนต์ของเซต A คือเซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของเอกภพสัมพัทธ์ แต่ไม่เป็นสมาชิกของ A เขียนแทนด้วย A ‘
• ผลต่างของเซต (Difference) : ผลต่างของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกที่เปีนสมาชิกของเซต A แต่ไม่เป็นสมาชิกของเซต B เขียนแทนด้วย A — B

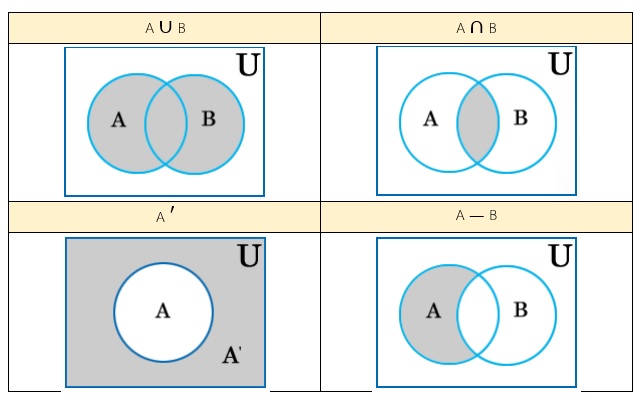
สมบัติของเซตที่ควรรู้