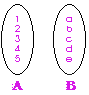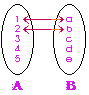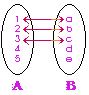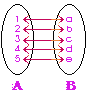เซตที่เท่ากัน (Equal Sets) คืออะไร
เซตที่เท่ากัน (Equal Sets) คือ เซตสองเซตจะเท่ากันก็ต่อเมื่อเซตทั้งสองมีสมาชิกเหมือนกัน สัญลักษณ์ เซต A เท่ากับ เซต B แทนด้วย A = B เซต A ไม่เท่ากับ เซต B แทนด้วย A ไม่เท่ากับ B
.
| เซตที่เท่ากัน (Equal Sets) | คือ เซตสองเซตจะเท่ากันก็ต่อเมื่อเซตทั้งสองมีสมาชิกเหมือนกัน สัญลักษณ์ เซต A เท่ากับ เซต B แทนด้วย A = B เซต A ไม่เท่ากับ เซต B แทนด้วย A  B B |
ตัวอย่าง
| A = {1, 2, 3, 4, 5} B = {1, 2, 3, 4, 3, 2, 5, 5, 5} |
เซต A มีสมาชิกเหมือนกับเซต B | A = B |
| C = {a, e, i, o, u} D = {i, o, u, e, o} |
เซต C มีสมาชิกเหมือนกับเซต D | C = D |
| E = {0, 1, 3, 5} F = {x | x  I+, x < 6} I+, x < 6} |
เซต E มีสมาชิก 4 ตัว คือ 0, 1, 3, 5 แต่เซต F มีสมาชิก 5 ตัว คือ 1, 2, 3, 4, 5 | E  F F |
| G = {สีแดง, สีน้ำเงิน, สีขาว} H = {สีแดง, สีน้ำเงิน, สีเหลือง} |
สีขาว  G แต่ สีขาว G แต่ สีขาว  H H |
G  H H |
| 2. เซตที่เทียบเท่ากัน (Equivalentl Sets) | คือ เซตที่มีจำนวนสมาชิกเท่ากัน และสมาชิกของเซตจับคู่กันได้พอดีแบบหนึ่งต่อหนึ่ง สัญลักษณ์ เซต A เทียบเท่ากับ เซต B แทนด้วย A  B B |
ตัวอย่าง
| A = {a, b, c, d, e} B = {1, 2, 3, 4, 5} |
A  B แต่เซตทั้งสองมีจำนวนสมาชิกเท่ากัน และสามารถจับคู่แบบ 1:1 ได้พอดี B แต่เซตทั้งสองมีจำนวนสมาชิกเท่ากัน และสามารถจับคู่แบบ 1:1 ได้พอดี
|
A  B B |
C = {x | x  I+} I+}D = {x | x = 2n , n = 1, 2, 3, …} |
C เป็นเซตจำนวนเต็มบวก {1, 2, 3, …} ส่วนเซต D เป็นเซตของจำนวนคู่ตั้งแต่ 2 ขึ้นไป {2, 4, 6, …} โดยสมาชิกของเซต C กับ D จับคู่แบบ 1:1 ได้พอดี 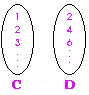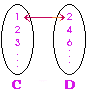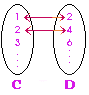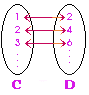 |
C  D D |
| หมายเหตุ | 1. ถ้า A = B แล้ว A  B B2. ถ้า A  B แล้ว ไม่อาจสรุปได้ว่า A = B B แล้ว ไม่อาจสรุปได้ว่า A = B |
ที่มา : ทวี บุญช่วย , วารสารไฮเอ็ด ม.ปลาย (วิทย์), ปีที่ 1 ฉ. 1 พฤษภาคม 2539