เซตและการดำเนินการของเซต
การดำเนินการทั้งสองแบบนี้เป็นพื้นฐานของการดำเนินการเรื่องเซตเราเรียกการรวมเซตสองเซตเข้าด้วยกันว่าผลผนวก และเรียกการเลือกส่วนที่ซ้ำกันระหว่างเซตสองเซตว่าผลตัด
ผลผนวก
A U B = { x, x เป็นสมาชิกของเซต A หรือ x เป็นสมาชิกของเซต B }
คุณสมบัติของผลผนวก
- A U A = A การนำเซตเดียวกับมารวมกันย่อมได้เซตเดิม
- A U ( B U C ) = ( A U B) U C การนำเซต B รวมกับเซต C จากนั้นนำไปรวมกันเซต A จะได้เซตเดียวกันกับการรวมเซต A และ เซต B แล้วไปรวมกับเซต C
- A U B = B U A การนำเซต A ไปรวมกับเซต B เป็นเซตเดียวกันกับ การนำเซต B ไปรวมกันเซต A
ผลตัด.
A ∩ B = { x, x เป็นสมาชิกของเซต A และ x เป็นสมาชิกของเซต B }
คุณสมบัติของผลผนวก
- A ∩ A = A การเลือกส่วนที่ซ้ำกันของเซตเดียวกันย่อมได้เซตเดิม
- A ∩ ( B ∩ C ) = ( A ∩ B) ∩ C การเลือกส่วนที่ซ้ำกันระหว่างเซต B กับเซต C จากนั้นนำไปเลือกส่วนที่ซ้ำกันกับเซต A จะได้เซตเดียวกันกับการเลือกส่วนที่ซ้ำกันระหว่างเซต A และ เซต B แล้วเลือกส่วนที่ซ้ำกันกับเซต C
- A ∩ B = B ∩ A การเลือกส่วนที่ซ้ำกันระหว่างเซต A กับเซต B เป็นเซตเดียวกันกับ การเลือกส่วนที่ซ้ำกันของเซต B กับเซต A
ผลต่าง
A – B = { x, x เป็นสมาชิกของเซต A แต่ x ไม่เป็นสมาชิกของเซต B }
นิยามข้างต้นเรากล่าวถึง x ไม่เป็นสมาชิกของเซต B เราสามารถรวบรวมสมาชิกทั้งหมดที่ไม่ใช้สมาชิกของเซตฺBและเรียกเซตนี้ว่าส่วนเติมเต็มของ B เขียนแทนด้วย BC นั้นคือ ถ้า x ไม่ใช่สมาชิกของเซต B แล้ว x จะต้องเป็นสมาชิกของ BC ดังนั้นนิยามของผลต่างสามารถเขียนในรูปของผลตัดได้ดังนี้
A – B = { x, x เป็นสมาชิกของเซต A แต่ x ไม่เป็นสมาชิกของเซต B }
A – B = { x, x เป็นสมาชิกของเซต A และ x เป็นสมาชิกของเซต BC }
A – B = A ∩ BC
ผลต่างสมมาตร
ผลตัดเป็นการดำเนินการโดยเลือกส่วนที่ซ้ำกันของเซตสองเซตแต่หากเราสนใจส่วนที่ไม่ซ้ำกันสามารถอธิบายได้ด้วยผลต่างสมมาตรของเซตสองเซตนั้นคือ
A Δ B = (A – B) U (B – A)
สรุปเซตและการดำเนินการของเซต
2.อินเตอร์เซคชัน (intersection)
3.คอมพลีเมนท์ (complement)
4.ผลต่าง (difference)

ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B
ตัวอย่างเช่น A ={1,2,3}
B= {3,4,5}
∴ A ∪ B = {1,2,3,4,5}
เราสามารถเขียนการยูเนี่ยนลงในแผนภาพได้ดังนี้
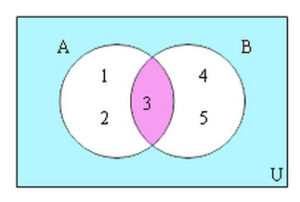
อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B
ตัวอย่างเช่น A ={1,2,3}
B = {3,4,5}
∴ A ∩ B = {3}
เราสามารถเขียนการอินเตอร์เซกชันลงในแผนภาพได้ดังนี้

คอมพลีเมนต์ (Complements) มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’
ตัวอย่างเช่น U = {1,2,3,4,5}
A ={1,2,3}
∴ A’ = {4,5}
สมบัติของการยูเนียน
ให้ A,B,C เป็นเซตย่อยของเอกภพสัมพัทธ์
1.) A∪Ø = A
2.) A∪B = B∪A
3.) A∪(B∪C) = (A∪B)∪C
4.) A∪A = A
การอินเตอร์เซกชัน (intersection)
เราจะใช้สัญลักษณ์ ∩ แทนการอินเตอร์เซกชัน
A∩B อ่านว่า A อินเตอร์เซกชัน B คือ เซตที่สร้างมาจากส่วนที่ A กับ B มีสมาชิกร่วมกัน
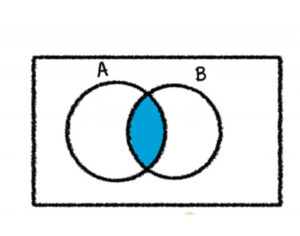
A∩B คือส่วนที่ A กับ B ซ้ำกัน
เช่น A = {1,2,3,4,5} B = {2,4,5,a,b} จะได้ว่า A∩B = {2,4,5}
A∩B คือส่วนที่ A กับ B ซ้ำกัน
สมบัติของการอินเตอร์เซกชัน
ให้ A,B,C เป็นเซตย่อยของเอกภพสัมพัทธ์
1.) A∩Ø = Ø
2.) A∩U = A
3.) A∩B = B∩A
4.) (A∩B)∩C = A∩(B∩C)
5.) A∩A = A
ตัวอย่างการยูเนียนและอินเตอร์เซกชัน
ให้ A,B,C เป็นเซตย่อยของเอกภพสัมพัทธ์ U
ให้แรเงาตามที่โจทย์กำหนด
1.) A∪B
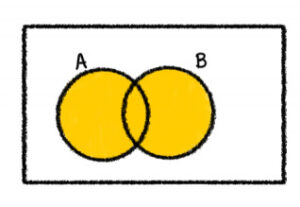
2.) A∩B
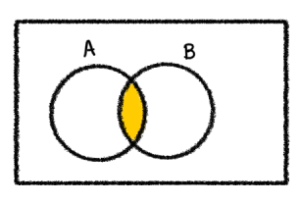
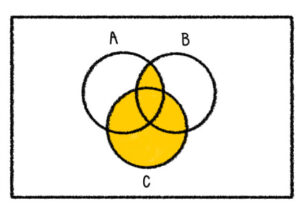
3.) (A∩B)∪C
เราจะทำในวงเล็บก่อน
4.) A∩B∩C
ส่วนเติมเต็ม (complement)
ให้A เป็นเซตย่อยของ U เราจะใช้ A′ แทน ส่วนเติมเต็มของ A

พูดให้เข้าใจง่าย A′ ก็คือ ส่วนที่ไม่ใช่ A
สมบัติของส่วนเติมเต็ม
ให้ A และ B เป็นเซตย่อยของ U
1.) (A′)′ = A
2.) A∩A′ = Ø
3.) A∪A′ = U
4.) (A∪B)′ = A′∩B′
5.) (A∩B)′ = A′∪B′
6.) Ø′ = U
7.) U′ = Ø
ผลต่างเซต (difference)
ให้ A และ B เป็นเซตย่อยของ U
ผลต่างของเซต A กับเซต B เขียนแทนด้วย A-B
A-B คือเซตที่มีสมาชิกของA แต่ไม่มีสมาชิกของ B
แหล่งที่มา
Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.
และ https://www.scimath.org/






