เซต ม.4 SET บทสรุป
สรุปเรื่อง เซต SET (ม.4)
เซต คือ กลุ่มของสิ่งต่างๆ เช่น เซตของสระในภาษาอังกฤษ เซตของจังหวัดในภาคกลาง
วิธีการเขียนเซตมี 2 แบบ คือ
- แบบแจกแจงสมาชิก การเขียนเซตแบบนี้จะเขียนสมาชิกทุกตัวของเซตลงในวงเล็บปีกกา “{ }” และใช้เครื่องหมายจุลภาค ” , ” คั่นระหว่างสมาชิกแต่ละตัว
- แบบบอกเงื่อนไข เป็นการเขียนโดยใช้ตัวแปรแทนสมาชิกแล้วกำหนดเงื่อนไขเกี่ยวกับตัวแปรนั้นเพื่อให้ทราบว่าตัวแปรนั้นแทนสมาชิกใดบ้าง
เซต (Sets) หมายถึง กลุ่มสิ่งของต่างๆ ไม่ว่าจะเป็น คน สัตว์ สิ่งของ หรือนิพจน์ทางคณิตศาสตร์ ซึ่งสามารถระบุสมาชิกในกลุ่มได้ และเรียก สมาชิกในกลุ่มว่า “สมาชิกของเซต”
การเขียนเซต
การเขียนเซตนิยมใช้อักษรตัวใหญ่เขียนแทนชื่อเซต และสามารถเขียนได้ 2แบบ
1. แบบแจกแจงสมาชิกของเซต
ตัวอย่างเช่น A = {1, 2, 3, 4, 5}
2. แบบบอกเงื่อนไขของสมาชิกในเซต
ตัวอย่างเช่น A = { x | x เป็นจำนวนเต็มบวกที่มีค่าน้อยกว่าหรือเท่ากับ 5}
เซตจำกัด
เซตจำกัด คือ เซตที่สามารถระบุจำนวนสมาชิกในเซตได้
ตัวอย่างเช่น A = {1, 2, 3, 4, 5} มีสมาชิก 5 สมาชิก
เซตอนันต์
เซตอนันต์ คือ เซตที่ไม่ใช่เซตจำกัด หรือเซตที่มีจำนวนสมาชิกมากมายนับไม่ถ้วน
ตัวอย่างเช่่น C = {…,-2,-1,0,1,2,…}
เซตที่เท่ากัน
เซต A และเซต B จะเป็น เซตที่เท่ากัน ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B และสมาชิกทุกตัวของเซต B เป็นสมาชิกทุกตัวของเซต A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A= B
ตัวอย่างเช่น A = {1, 2, 3, 4, 5}
B = { x | x เป็นจำนวนนับที่มีค่าน้อยกว่าหรือเท่ากับ 5}
เซตว่าง
เซตว่าง คือ เซตที่ไม่มีสมาชิก หรือมีจำนวนสมาชิกในเซตเป็นศูนย์ สามารถเขียนแทนได้ด้วยสัญลักษณ์ {} หรือ Ø
ตัวอย่างเช่่น A = {x | x เป็นจำนวนเต็ม และ 1 < x < 2}
B = { x | x เป็นจำนวนเต็มบวก และ x + 1 = 0 }
เอกภพสัมพัทธ์
เอกภพสัมพัทธ์ คือ เซตที่ประกอบด้วยสมาชิกทั้งหมดของสิ่งที่เราต้องการจะศึกษา สามารถเขียนแทนได้ด้วยสัญลักษณ์ u
ตัวอย่างเช่่น U = {…,-2,-1,0,1,2,…}
หรือU = {x | x เป็นจำนวนเต็ม}
สัญลักษณ์เกี่ยวกับเซต
- ∈ แทน เป็นสมาชิกของเซต
- ∉ แทน ไม่เป็นสมาชิกของเซต
- Ø หรือ { } แทน การเป็นเซตว่าง
- ⊂ แทน เป็นสับเซตของเซต
- ⊄ แทน ไม่เป็นสับเซตของเซต
- ∪ แทนยูเนียน คือ การรวมสมาชิกของเซตหลายเซตมารวมกัน
- ∩ แทน อินเตอร์เซกชัน
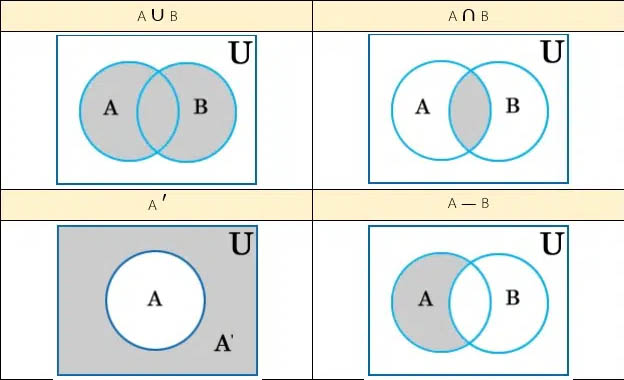
สัญลักษณ์เกี่ยวกับเซต
- ∈ แทน เป็นสมาชิกของเซต
- ∉ แทน ไม่เป็นสมาชิกของเซต
- Ø หรือ { } แทน การเป็นเซตว่าง
- ⊂ แทน เป็นสับเซตของเซต
- ⊄ แทน ไม่เป็นสับเซตของเซต
- ∪ แทนยูเนียน คือ การรวมสมาชิกของเซตหลายเซตมารวมกัน
- ∩ แทน อินเตอร์เซกชัน
เพิ่มเติม
- R แทน เซตของจำนวนจริง
- Iº แทน จำนวนเต็มศูนย์
- I¯แทน เซตของจำนวนเต็มลบ
- N แทน เซตของจำนวนนับ
- I+ แทน เซตของจำนวนเต็มบวก
- > เครื่องหมายน้อยกว่า
- < เครื่องหมายมากกว่า
- ≤ เครื่องหมายมากกว่าหรือเท่ากับ
- ≥ เครื่องหมายน้อยกว่าหรือเท่ากับ
- ” | ” อ่านว่าโดยที่หรือซึ่ง
- เซตจำกัด คือ เซตที่มีจำนวนสมาชิกเท่ากับศูนย์หรือเท่ากับจำนวนเต็มบวกใดๆ
- เซตอนันต์ คือ เซตที่ไม่สามารถบอกจำนวนสมาชิกของเซตได้ (มีมากแบบไม่มีสิ้นสุด)
- เซตว่าง คือ เซตที่ไม่มีสมาชิก
Ex.6 A={1,2} B={1,2,3,4}
ตอบ A⊂B และ B⊄A
- A เป็นสับเซตของ B เพราะ A มีเหมือนกับ B ทุกตัว ก็คือ A มี 1,2 และ B ก็มี 1,2 เช่นกัน
- B ไม่เป็นสับเซตของ A เพราะ B มีไม่เหมือน A ทุกตัว ก็คือ B มี 1,2,3,4 ส่วน A มีแค่ 1,2
- และถ้าโจทย์ถามว่า {1,2} ⊂ B ใช่หรือไม่ คำตอบคือใช่ เพราะ B ก็มีทั้ง 1,2
- ถ้าโจทย์ถามว่า {1,2,5} ⊂ B ใช่หรือไม่ คำตอบคือไม่ใช่ เพราะ B ไม่มีเลข 5
- {1,2,3,4}⊂ B ใช่หรือไม่ คำตอบคือใช่ {1,2,3,4} เป็นสับเซตของ B แต่เป็นสับเซตไม่แท้ ถ้าหากเหมือนกันทุกตัวจะเป็นสับเซตไม่แท้ทันที
- {1,2} เป็นสับเซตของ B และเป็นสับเซตแท้ ก็คือถ้าไม่เหมือนครบทุกตัวจะขาดหนึ่งตัวหรือสองหรือกี่ตัวก็แล้วแต่มันก็คือสับเซตแท้
-ขอบคุณข้อมูล https://news.trueid.net/