แผนภาพเวนน์-ออยเลอร์
การใช้แผนภาพเวนน์–ออยเลอร์ ในการตรวจสอบความสมเหตุสมผล
เราจะวาดแผนภาพตามสมมติฐานที่เป็นไปได้ แล้วพิจารณาว่าแผนภาพแต่ละกรณีแสดงผลสรุปตามที่สรุปไว้หรือไม่ ถ้าทุกกรณีแสดงผลตามที่กหนด แสดงว่าสมเหตุสมผล ถ้ามีแผนภาพที่ไม่แสดงผลตามที่สรุปไว้ การสรุปนั้นไม่สมเหตุสมผล โดยจะใช้การอ้างเหตุผลโดยตรรกบทของตรรกศาสตร์เข้ามาตรวจสอบ
ในการใช้แผนภาพเพื่อตรวจสอบความสมเหตุสมผล จะต้องวาดแผนภาพตามเหตุผลหรือสมมติฐานทุกกรณีที่เป็นไปได้ ถ้าทุกกรณีแสดงผลตามที่กำหนด จะได้ว่าข้อสรุปนั้น สมเหตุสมผล แต่ถ้ามีบางกรณีที่ไม่สอดคล้องกับผลสรุปแล้ว ผลสรุปนั้นจะไม่สมเหตุผมผล
แผนภาพเวนน์-ออยเลอร์ (Venn-Euler diagram)
แผนภาพเวนน์-ออยเลอร์ เป็นแผนภาพแสดงความเกี่ยวข้องของเซตต่าง ๆ ซึ่งชื่อที่ใช้เรียกเป็นชื่อของนักคณิตศาสตร์สองคน คือ จอห์น เวนน์ และ เลโอนาร์ด ออยเลอร์
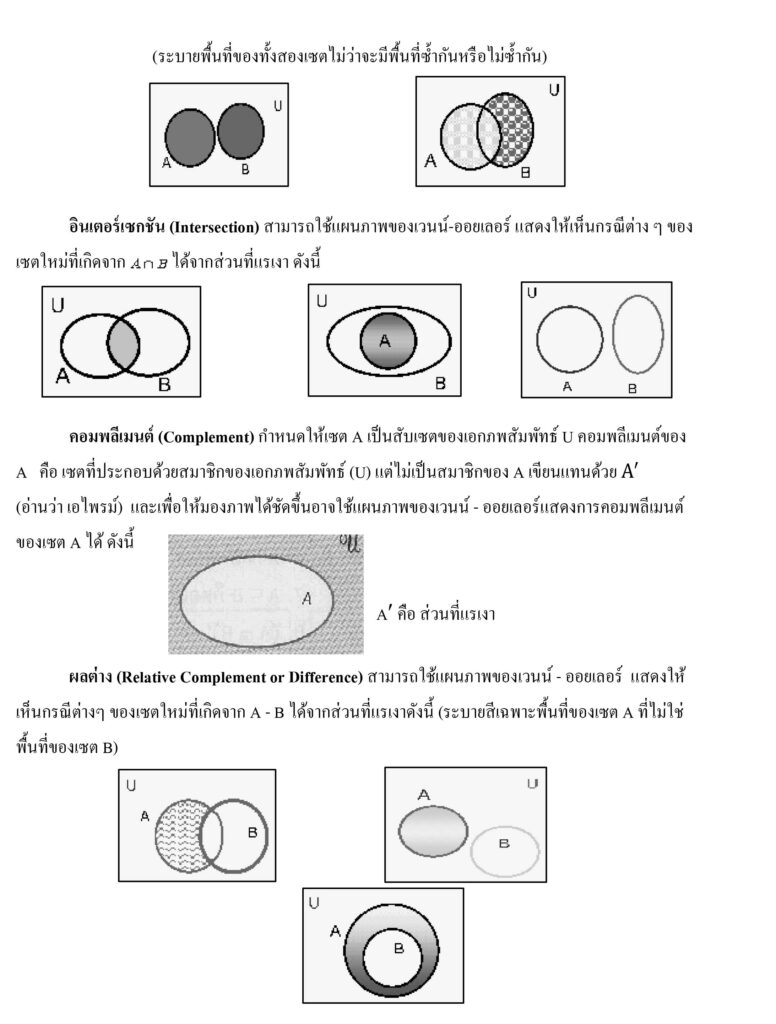
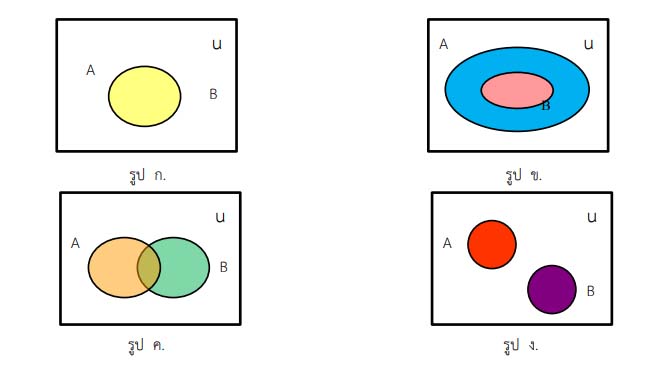
การเขียนแผนภาพเวนน์-ออยเลอร์
การเขียนแผนภาพเวนน์-ออยเลอร์ มักเขียนแทนเอกภพสัมพัทธ์ U ด้วยสี่เหลี่ยมผืนผ้าหรือรูปปิดใด ๆ ส่วนเซต A,B,C,D,… ซึ่งเป็นเซตย่อยของ U อาจเขียนแทนด้วยวงกลมหรือวงรีหรือรูปปิดใด ๆ โดยให้ภาพทื่แทนเซตย่อยอยู่ในรูปสี่เหลี่ยมผืนผ้าที่แทนเอกภพสัมพัทธ์
ถ้ากำหนดให้ U = {1,2,3,4,5,6,7,8,9,10}
A = {1,2,3} , B = {1,2,3,4,5} , C = {3,5,6,7}