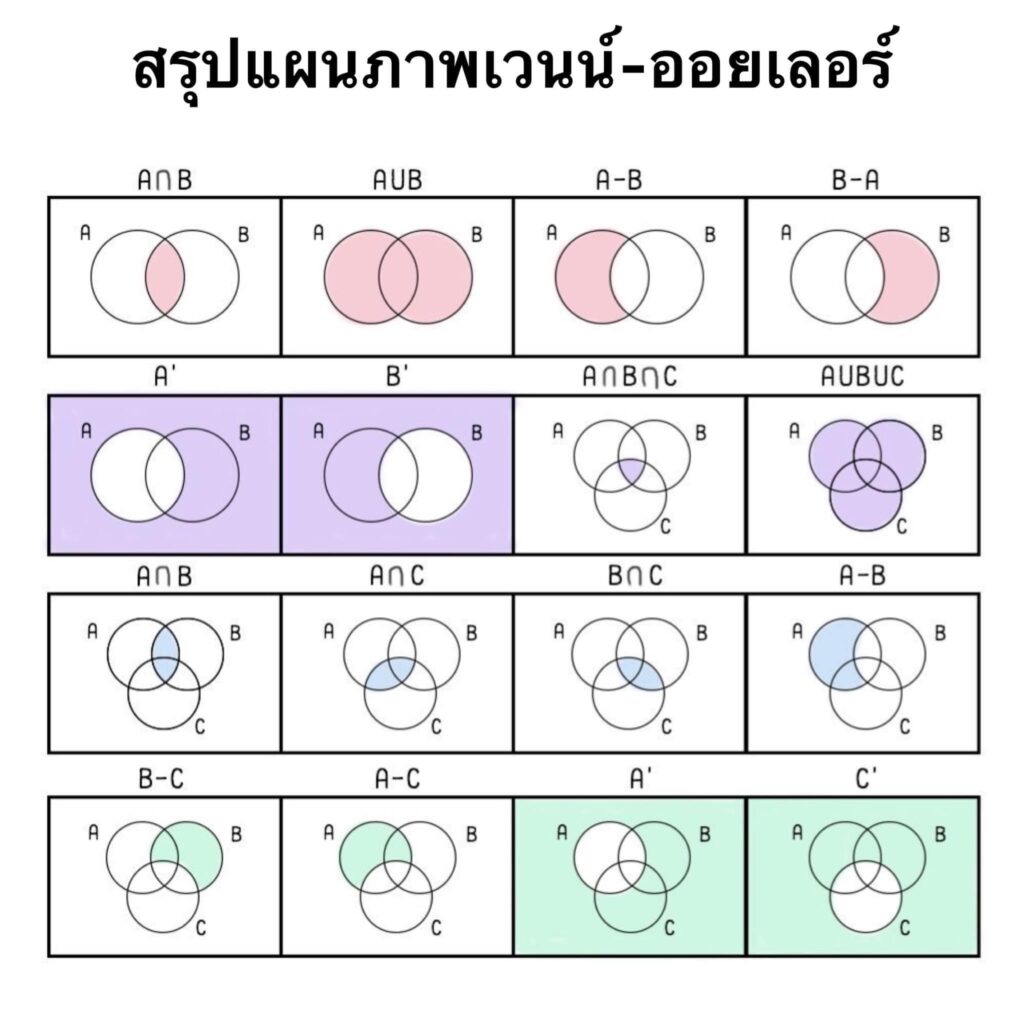
แผนภาพเวนน์-ออยเลอร์ (Venn-Euler diagram)

การเขียนแผนภาพเวนน์–ออยเลอร์

การเขียนแผนภาพเวนน์–ออยเลอร์มักเขียนแทนเอกภพสัมพัทธ์U ด้วยสี่เหลี่ยมผืนผ้าหรือรูปปิดใดๆ ส่วนเซต A,B,C,D,… ซึ่งเป็นเซตย่อยของ Uอาจเขียนแทนด้วยวงกลมหรือวงรีหรือรูปปิดใดๆโดยให้ภาพที่แทนเซตย่อยอยู่ในรูปสี่เหลี่ยมผืนผ้าที่แทนเอกภพสัมพัทธ์

การพิจารณาเกี่ยวกับเซตจะง่ายขึ้น ถ้าเราใช้แผนภาพของเวนน์-ออยเลอร์ เข้ามาช่วย หลักการเขียนแผนภาพมีดังนี้

1. ใช้รูปสี่เหลี่ยมผืนผ้าหรือสี่เหลี่ยมมุมฉากแทนเอกภพสัมพัทธ์

2. ใช้วงกลมหรือวงรีหรือรูปปิดใด ๆ แทนเซตต่าง ๆ ที่เป็นสมาชิกของ และเขียนภายในสี่เหลี่ยมผืนผ้า

เป็นแผนภาพที่นิยมใช้เขียนเพื่อแสดงความสัมพันธ์ของเซต เพื่อให้ดูง่ายและชัดเจนมากขึ้น ปกติจะกำหนดเอกภพสัมพัทธ์ด้วยกรอบสี่เหลี่ยมมุมฉาก ภายในนั้นมีเซตซึ่งอาจเขียนเป็นวงกลม วงรี หรือรูปปิดอื่นๆ

สมมติเรามีเซตต่างๆ ดังภาพต่อไปนี้

จากรูป (a): A = {1, 2} B = {3, 4, 5} จะเห็นได้ว่า A และ B ไม่มีสมาชิกร่วมกันเลย

ส่วนรูป (b): C = {a, b,c,d} D = {c,d, e, f, g} จะเห็นได้ว่าทั้งสองเซตนี้มีสมาชิกบางตัวร่วมกัน

สำหรับรูป (c): E = {1,2, 3} F = {1,2}

การดำเนินการของเซต (Operation of set)

เอกภพสัมพัทธ์ (Relative Universe) คือ เซตที่ใช้กำหนดขอบเขตของสิ่งต่าง ๆ ที่จะกล่าวถึง โดยมีข้อตกลงว่าจะไม่กล่าวถึงสิ่งอื่นใดซึ่งนอกเหนือจากสิ่งที่เซตนี้กำหนดไว้ เขีนแทนด้วย U ถ้ากล่าวถึงเซตของจำนวนโดยไม่กำหนดเอกภพสัมพัทธ์ ให้ถือว่าเอกภพสัมพัทธ์คือเซตของจำนวนจริง

การดำเนินการของเซต (Operation of set) เป็นการสร้างเซตใหม่ขึ้นจากเซตที่กำหนดให้ ได้แก่
1. ยูเนียน (Union)
A U B คือ เซตที่ประกอบด้วยสมาชิกของเซต A หรือเซต B หรือทั้งสองเซต
2.อินเตอร์เซกชัน (Intersection)
A ∩ B คือ เซตที่ประกอบด้วยสมาชิกของเซต A และเซต B ที่ซ้ำกัน
3. ผลต่าง (Difference)
A – B คือ เซตที่ประกอบด้วยสมาชิกของเซต A โดยที่ไม่เป็นสมาชิกของเซต B
4. คอมพลีเมนต์ (Complement)
A’ คือ เซตที่ประกอบด้วยสมาชิกของเอกภพสัมพัทธ์ U แต่ไม่เป็นสมาชิกของ A

ยูเนียน (Union)

– ยูเนียน (Union) : ยูเนียนของเซต A และเซต B จะได้เซตใหม่ ซึ่งมีสมาชิกของเซต A หรือเซต B หรือทั้งสองเซต

“ ยูเนียนของเซตA และเซต B เขียนแทนด้วย A B ”

A B = {x| x A หรือ x เ ป็นสมาชิกของทั้งสองเซต}

เช่น A = {1,3,5} และ B = {3,6,9}

จะได้ A B ={1,3,5,6,9}

ดังนั้น ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B

ตัวอย่างเช่น A ={1,2,3}

B = {3,4,5}

∴ A U B = {1,2,3,4,5}

อินเตอร์เซกชัน

– อินเตอร์เซกชัน (Intersection): อินเตอร์เซกชันของเซต A และเซต B จะได้เซตใหม่ ซึ่งสมาชิกเป็นสมาชิกของเซตทั้งเซต A และเซต B

“ อินเตอร์เซกชันของเซตA และเซต B เขียนแทนด้วย A B ”

A B = {x| x A และ x B}

เช่น A = {1,2,3,4,} , B = {2,4,6} และ C = {0,1}

จะได้ A B = {2,4}

A C = {1}

B C = {}

ดังนั้น อินเตอร์เซกชัน (Intersection) มีนิยามคือเซต A อินเตอร์เซกชันเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B

ตัวอย่างเช่น A ={1,2,3}

B = {3,4,5}

∴ A ∩ B = {3}

Set Operator ( การกระทำของเซต)

การดำเนินการของเซต ( Operation With set ) เป็นการสร้างเซตขึ้นมาใหม่จากการนำเซตที่กำหนดให้ มาดำเนินการตามต้องการ ซึ่งจะมีการดำเนินการหลายแบบ เช่น ยูเนียนของเซต อินเตอร์เซกชันของเซต คอมพลีเมนต์ของเซต และผลต่าง

ยูเนียน ( Union )

มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ

เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B

ตัวอย่างเช่น A ={1,2,3}

B = {3,4,5}

∴ A U B = {1,2,3,4,5}

อินเตอร์เซกชัน ( Intersection )

มีนิยามคือเซต A อินเตอร์เซกชันเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B

ตัวอย่าง เช่น A ={1,2,3}

B = {3,4,5}

∴ A ∩ B = {3}

คอมพลีเมนต์ ( Complements )

มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ แล้ว คอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’

ตัวอย่างเช่น U = {1,2,3,4,5}

A ={1,2,3}

∴ A’ = {4,5}

ผลต่าง ( Differnce )

บทนิยาม ถ้า A และ B ต่างก็เป็นสับเซตของเซต U ผลต่างของเซต A และ B คือ เซตที่ประกอบด้วยสมาชิกของเซต A แต่ไม่เป็นสมาชิกของ B เขียนแทนด้วย A – B

ตัวอย่าง กำหนดเซต A และ B จงหา A – B

กำหนด A = {3, 9}

B = {4, 6, 7}

A – B = {3, 9}