เนื้อหาคณิตศาสตร์ ม. 1 เทอม 1 มีเรียนอะไรมาดูกัน…
บทเรียนเรื่อง ตัวหารร่วมมากและตัวคูณร่วมน้อย
บทเรียนย่อย
– การหาตัวคูณร่วมน้อย (ค.ร.น.) (animation)
แบบทดสอบความรู้
– ค.ร.น. และ ห.ร.ม.
– หรม.
– คูณร่วมน้อยและการนำไปใช้
– หารร่วมมากและการนำไปใช้
1.ระบบจำนวนเต็ม
บทเรียนย่อย
– จำนวนและการดำเนินการ
– สมบัติของจำนวนนับและจำนวนเต็ม
– ตัวประกอบและตัวประกอบร่วม (animation)
– การแยกตัวประกอบและจำนวนตัวประกอบ (animation)
– การแยกตัวประกอบ
แบบทดสอบความรู้
– ระบบจำนวนเต็ม
– สมบัติจำนวนนับ
– สมบัติของจำนวนนับ
– แบบฝึกคิดเลขในใจ ระดับ 5 ชั้น ม. 1 – ม. 3
2. เลขยกกำลัง
บทเรียนย่อย
– เลขยกกำลัง (เนื้อหา)
– เลขยกกำลัง
– เลขยกกำลัง ตอนที่ 1
– เลขยกกำลัง ตอนที่ 2
– ตะลุยโจทย์ เรื่อง เลขยกกำลัง
แบบทดสอบความรู้
– เลขยกกำลัง
3. พื้นฐานทางเรขาคณิต
บทเรียนย่อย
– เรขาคณิต 2 มิติ
– ทฤษฎีบทพีทาโกรัส
ระบบจำนวนเต็ม
สรุป
ตัวตั้ง – ตัวลบ = ตัวตั้ง + จำนวนตรงข้ามของตัวลบ นั่นคือ เมื่อ a และ b แทนจำนวนใดๆ
a –b = a + จำนวนตรงข้ามของ b หรือ a – b = a + (-b)
การคูณและการหารจำนวนเต็ม
การคูณและการหารจำนวนเต็มมีหลักการในการคูณ/หารของเครื่องหมาย + / – ดังนี้
(+) x (+) = + และ (+) ÷ (+) = +
กล่าวคือ จำนวนเต็มบวก x จำนวนเต็มบวก = จำนวนเต็มบวก และ จำนวนเต็มบวก ÷ จำนวนเต็มบวก = จำนวนเต็มบวก
(+) x (-) = – และ (+) ÷ (-) = –
กล่าวคือ จำนวนเต็มบวก x จำนวนเต็มลบ = จำนวนเต็มลบ และ จำนวนเต็มบวก ÷จำนวนเต็มลบ = จำนวนเต็มลบ
(-) x (+) = – และ (-) ÷ (+) = –
กล่าวคือ จำนวนเต็มลบ x จำนวนเต็มบวก = จำนวนเต็มลบ และ จำนวนเต็มลบ ÷ จำนวนเต็มบวก = จำนวนเต็มลบ
(-) x (-) = + และ (-) ÷ (-) = +
กล่าวคือ จำนวนเต็มลบ x จำนวนเต็มลบ = จำนวนเต็มบวก และ จำนวนเต็มลบ ÷ จำนวนเต็มลบ = จำนวนเต็มบวก
หรืออาจกล่าวได้ว่า
– เครื่องหมายเหมือนกัน คูณ / หาร กันจะได้คำตอบเป็นจำนวนเต็มบวก
– เครื่องหมายต่างกัน คูณ / หาร กันจะได้คำตอบเป็นจำนวนเต็มลบ
การคูณจำนวนเต็ม
1). การคูณจำนวนเต็มบวกด้วยจำนวนเต็มบวก
เช่น 3 x 5 = 5 + 5 + 5 = 15
หรือ 7 x 4 = 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28
การคูณจำนวนเต็มบวกด้วยจำนวนเต็มบวกนั้น ได้คำตอบเป็นจำนวนเต็มบวกที่มีค่าสัมบูรณ์เท่ากับผลคูณของค่าสัมบูรณ์ของสองจำนวนนั้น
2). การคูณจำนวนเต็มบวกด้วยจำนวนเต็มลบ
เช่น 3 x (-8) = (-8) + (-8) + (-8) = -24
หรือ 2 x (-7) = (-7) + (-7) = -14
การคูณจำนวนเต็มบวกด้วยจำนวนเต็มลบ ได้คำตอบเป็นจำนวนเต็มลบที่มีค่าสัมบูรณ์เท่ากับผลคูณของค่าสัมบูรณ์ของสองจำนวนนั้น
3). การคูณจำนวนเต็มลบด้วยจำนวนเต็มบวก
เช่น (-7) x 4 = 4 x (-7) (สมบัติการสลับที่การคูณ) = (-7) + (-7)+ (-7) + (-7) = -28
การคูณจำนวนเต็มลบด้วยจำนวนเต็มบวก ได้คำตอบเป็นจำนวนเต็มลบที่มีค่าสัมบูรณ์เท่ากับผลคูณของค่าสัมบูรณ์ของสองจำนวนนั้น
4). การคูณจำนวนเต็มลบด้วยจำนวนเต็มลบ
เช่น (-3) x (-5) = 15 ( -11) x (-20) = 220
การคูณจำนวนเต็มลบด้วยจำนวนเต็มบวก ได้คำตอบเป็นจำนวนเต็มลบที่มีค่าสัมบูรณ์เท่ากับผลคูณของค่าสัมบูรณ์ของสองจำนวนนั้น
เลขยกกำลัง
เลขยกกำลัง คือ การเขียนตัวเลขที่มีการคูณซ้ำหลาย ๆครั้งในรูปแบบย่อให้มีความยาวที่สั้นลงทำให้สามารถอ่านได้เข้าใจได้ง่ายกว่าการเขียนจำนวนมากและทำให้การคำนวณทางคณิตศาสตร์ง่ายขึ้นในบางรูปแบบโดยการเขียน เลขยกกำลัง จะมีส่วนประกอบทั้งหมด 2 ส่วน คือ
- ฐานของเลขยกกำลัง
- เลขชี้กำลัง
ถ้าจำนวนที่คูณตัวเองซ้ำกันหลาย ๆ ตัว เราจะเขียนจำนวนเหล่านั้นออกมาในรูปของเลขยกกำลัง โดยจำนวนที่คูณตัวเองซ้ำ ๆ จะเรียกว่า “ฐาน” และจำนวนตัวที่คูณ จะเรียกว่า “เลขชี้กำลัง” เพื่อให้เข้าใจมากยิ่งขึ้น เพื่อน ๆ ลองนึกถึงการพับกระดาษ 1 แผ่น
พับกระดาษ 1 ครั้ง กระดาษถูกแบ่งออกเป็น 2 ส่วน
พับกระดาษ 2 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 = 4 ส่วน
พับกระดาษ 3 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 x 2 = 8 ส่วน
พับกระดาษ 10 ครั้ง กระดาษถูกแบ่งออกเป็น 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 1,024 ส่วน
กระดาษพับซ้อนกัน 1,024 ทบนี่หนามาก ๆ เลย และในชีวิตจริง ถ้าต้องเขียน 2 x 2 x 2 x … x 2 ให้ครบตามต้องการก็คงจะเหนื่อยและเสียเวลามาก ๆ นักคณิตศาสตร์จึงนิยมเขียนออกมาในรูปของ “เลขยกกำลัง” ซึ่งประกอบไปด้วยฐานและเลขชี้กำลัง เราสามารถเขียน 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 ให้อยู่ในรูปเลขยกกำลังได้ว่า 210 ซึ่ง 2 คือฐาน และ 10 คือเลขชี้กำลัง และจะอ่าน 210 ว่า…
2 กำลัง 10
2 ยกกำลัง 10
หรือ กำลัง 10 ของ 2
เลขยกกำลัง ฐาน และเลขชี้กำลัง
จำนวนที่สามารถเป็นฐานได้มีหลายรูปแบบ เช่น จำนวนเต็มบวก จำนวนเต็มลบ เศษส่วน ทศนิยม ยกตัวอย่างเช่น 24 (-2)4 (![]() )2 0.45
)2 0.45
ข้อสังเกต: อ่านไม่เหมือนกัน ผลลัพธ์ไม่เท่ากัน
ลบสองทั้งหมดยกกำลังสี่
(-2)4 = (-2)(-2)(-2)(-2) = 16
ลบสองยกกำลังสี่
-24 = – (2 x 2 x 2 x 2) = -16
จะเห็นว่า (-2)4 มีค่าไม่เท่ากับ -24 แค่ใส่วงเล็บ ผลลัพธ์ก็ต่างกันแล้ว ดังนั้นเพื่อน ๆ ต้องระวังการใส่วงเล็บให้ดีนะ เราลองมาดูตัวอย่างอื่น ๆ เพิ่มกันดีกว่า
54 = 5 x 5 x 5 x 5 = 625
(5)4 = (5)(5)(5)(5) = 625
-54 = -(5 x 5 x 5 x 5) = -(625) = -625
(-5)4 = (-5)(-5)(-5)(-5) = (25)(25) = 625
กรณีนี้ เลขชี้กำลังเป็นจำนวนคู่ สำหรับฐานที่เป็นจำนวนลบ จะเห็นว่า (-5)4 เท่ากับ 54 แต่ไม่เท่ากับ -54 อย่าลืมสังเกตให้ดีนะว่าเครื่องหมายลบอยู่ข้างในหรือข้างนอกวงเล็บ
53 = 5 x 5 x 5 = 125
-53 = -(5 x 5 x 5) = -125
(-5)3 = (-5)(-5)(-5) = -125
กรณีนี้ เลขชี้กำลังเป็นจำนวนคี่ สำหรับฐานที่เป็นจำนวนลบ จะเห็นว่า (-5)3 เท่ากับ -53 แต่ (-5)3 ไม่เท่ากับ 53
พื้นฐานทางเรขาคณิต
รูปเรขาคณิตสองมิติ ( two – dimensional geometric figure ) แบ่งออกเป็น 2 กลุ่มใหญ่ๆ ตามลักษณะของขอบหรือด้านของรูป ได้แก่ กลุ่มที่มีขอบหรือด้านของรูปเป็นส่วนของเส้นตรง กลุ่มนี้คือ “รูปหลายเหลี่ยม ( polygon )” และกลุ่มที่มีขอบหรือด้านเป็นเส้นโค้งงอ เช่น รูปวงกลม และรูปวงรี เป็นต้น กลุ่มนี้ไม่มีชื่อเรียกโดยเฉพาะ
รูปหลายเหลี่ยม (Polygon) เป็นรูปปิดที่เกิดจากส่วนของเส้นตรงตั้งแต่ 3 เส้นขึ้นไป โดยที่จุด A, B, C, … , P, Q,… เป็นจุดที่แตกต่างกันบนระนาบ และไม่มี 3 จุดใดอยู่ร่วมส่วนของเส้นตรงเดียวกัน เรียกว่า “ด้านของรูปหลายเหลี่ยม” จุด A, B, C, … , P, Q,… เรียกว่า “จุดยอด” จำนวนมุมในรูปหลายเหลี่ยมจะเท่ากับจำนวนด้านของรูปหลายเหลี่ยม ส่วนของเส้นตรงที่ลากเชื่อมจุดยอดที่ไม่ใช่ปลายของส่วนของเส้นตรงเดียวกัน เรียกว่า “เส้นทแยงมุม ( diagonal )”
รูปหลายเหลี่ยมด้านเท่ามุมเท่า ( regular polygon ) คือ รูปหลายเหลี่ยมที่มีด้านทุกด้านยาวเท่ากันและมุมทุกมุมมีขนาดเท่ากัน
รูปสามเหลี่ยม (Triangle) เป็นรูปหลายเหลี่ยมชนิดหนึ่ง ประกอบด้วยด้านที่เป็นส่วนของเส้นตรง 3 เส้น ส่วนของเส้นตรงทั้งสามนี้ต้องอยู่บนระนาบเดียวกัน ซึ่งทำให้เกิดมุม 3 มุม

ที่มาของภาพ : http://www.trueplookpanya.com/new/cms_detail/knowledge/930-00/
ข้อสังเกต
1. ความสูงของรูปสามเหลี่ยมเป็นเท่าใด ขึ้นอยู่กับว่าให้ด้านใดเป็นฐานของรูปสามเหลี่ยม ความสูงมีได้ 3 ค่า ซึ่งอาจจะมีค่าต่างกัน
2. ส่วนสูงของรูปสามเหลี่ยม อาจจะอยู่ในหรือนอกรูปสามเหลี่ยมก็ได้
ชนิดของรูปสามเหลี่ยม การจำแนกรูปสามเหลี่ยม มีเกณฑ์ในการพิจารณาดังนี้
1. พิจารณาจากความยาวของด้านจำแนกได้ดังนี้
1.1 รูปสามเหลี่ยมด้านเท่า ( equilateral triangle ) คือ รูปสามเหลี่ยมที่มีด้านทั้งสามยาวเท่ากัน
1.2 รูปสามเหลี่ยมหน้าจั่ว ( isosceles triangle ) คือ รูปสามเหลี่ยมที่มีด้านสองด้านยาวเท่ากัน
1.3 รูปสามเหลี่ยมด้านไม่เท่า ( scalene triangle) คือ รูปสามเหลี่ยมที่ไม่มีด้าน 2 ด้านใดยาวเท่ากัน
2. พิจารณาจากขนาดของมุม จำแนกได้ดังนี้
2.1 รูปสามเหลี่ยมมุมแหลม ( acute triangle ) คือ รูปสามเหลี่ยมที่มีมุมทั้งสามมีขนาดเล็กกว่า มุมฉาก
2.2 รูปสามเหลี่ยมมุมฉาก ( right triangle ) คือ รูปสามเหลี่ยมที่มีมุมมุมหนึ่งมีขนาดเท่ากับ มุมฉาก
2.3 รูปสามเหลี่ยมมุมป้าน ( obtuse triangle ) คือ รูปสามเหลี่ยมที่มีมุมมุมหนึ่งมีขนาดใหญ่กว่ามุมฉาก
หมายเหตุ รูปสามเหลี่ยมมุมแหลมนอกระบบยูคลิด คือ รูปสามเหลี่ยมที่มุมทั้งสามมีขนาดเล็กกว่ามุมฉาก ซึ่งเป็นรูปสามเหลี่ยมที่ไม่ได้เกิดจากส่วนของเส้นตรงสามเส้น และมุมภายในทั้งสามรวมกันได้น้อยกว่า 180o
รูปสี่เหลี่ยม (Quadrilateral) เป็นเส้นโค้งปิดเชิงเดียว ประกอบด้วยส่วนของเส้นตรง 4 เส้นที่อยู่บนระนาบเดียวกัน ส่วนของเส้นตรงแต่ละเส้น เรียกว่า ด้านของรูปสี่เหลี่ยม รูปสี่เหลี่ยมใดๆ ประกอบด้วยด้าน 4 ด้าน และมุม 4 มุม

ที่มาของภาพ : http://www.myfirstbrain.com/teacher_view.aspx?ID=45982
– ส่วนประกอบของรูปสี่เหลี่ยม
1. ด้านประชิด ( adjacent sides ) คือ ด้านสองด้านของรูปสี่เหลี่ยมที่มีจุดปลายร่วมกัน 1 จุด
2. ด้านตรงข้าม ( opposite sides ) คือ ด้านสองด้านของรูปสี่เหลี่ยมที่ไม่มีจุดปลายร่วมกัน
3. มุมประชิด ( adjacent angles ) คือ มุมสองมุมของรูปสี่เหลี่ยมที่มีแขนของมุมร่วมกันอยู่แขนหนึ่ง
4. มุมตรงข้าม ( opposite angles ) คือ มุมสองมุมของรูปสี่เหลี่ยมที่ไม่มีแขนของมุมร่วมกัน
5. มุมภายในของรูปสี่เหลี่ยม ขนาดของมุมภายในทั้งสี่รวมกันได้ 360o
6. เส้นทแยงมุม ( diagonal ) คือ ส่วนของเส้นตรงที่มีจุดปลายทั้งสองอยู่ที่จุดยอดของมุมตรงข้าม
– ชนิดของรูปสี่เหลี่ยม
1. รูปสี่เหลี่ยมด้านขนาน ( parallelogram ) คือ รูปสี่เหลี่ยมที่ด้านตรงข้ามขนานกันทั้ง 2 คู่ ซึ่งทำให้ด้านตรงข้ามยาวเท่ากันด้วย เส้นทแยงมุมทั้งสองแบ่งครึ่งซึ่งกันและกัน แต่ยาวไม่เท่ากัน
2. รูปสี่เหลี่ยมคางหมู( trapezoid ) คือ รูปสี่เหลี่ยมที่มีด้านตรงข้ามขนานกันเพียงคู่เดียว
3. รูปสี่เหลี่ยมผืนผ้า ( rectangle ) คือ รูปสี่เหลี่ยมด้านขนานที่มีมุมเป็นมุมฉาก ด้านประชิดยาวไม่เท่ากัน มีผลทำให้ด้านตรงข้ามขนานกันและยาวเท่ากัน เส้นทแยงมุมยาวเท่ากันและแบ่งครึ่งซึ่งกันและกัน
4. รูปสี่เหลี่ยมจัตุรัส ( square ) คือ รูปสี่เหลี่ยมผืนผ้าที่มีด้านทั้งสี่ยาวเท่ากัน มีผลทำให้เส้นทแยงมุมยาวเท่ากันแบ่งครึ่งซึ่งกันและกัน และตัดกันเป็นมุมฉาก
5. รูปสี่เหลี่ยมขนมเปียกปูน ( rhombus ) คือ รูปสี่เหลี่ยมด้านขนานที่มีด้านทั้งสี่ยาวเท่ากัน เส้นทแยงมุมยาวไม่เท่ากัน แต่แบ่งครึ่งซึ่งกันและกัน และตัดกันเป็นมุมฉาก
6. รูปสี่เหลี่ยมรูปว่าว ( kite ) คือ รูปสี่เหลี่ยมที่มีด้านประชิดยาวเท่ากันเพียง 2 คู่เท่านั้น เส้นทแยงมุมยาวไม่เท่ากัน ไม่แบ่งครึ่งซึ่งกันและกัน แต่ตัดกันเป็นมุมฉาก

รูปเรขาคณิตสามมิติ ( three – dimensional geometric figure ) คือ สิ่งต่างๆ รอบตัวเราที่มีลักษณะสำคัญคือ มีความกว้าง ความยาว และความหนาหรือความสูง การจำแนกรูปเรขาคณิตสามมิติ พิจารณาจากรูปร่างลักษณะของรูปเรขาคณิตที่ประกอบกันเป็นทรง
1. ปริซึม (Prism) คือ รูปเรขาคณิตสามมิติที่มีหน้าตัด (ฐาน) ทั้งสองเป็นรูปหลายเหลี่ยมที่เท่ากันทุกประการ และอยู่ในระนาบที่ขนานกัน มีหน้าข้างเป็นรูปสี่เหลี่ยมด้านขนาน
ทฤษฎีบทพีทาโกรัส
1.1 ทฤษฎีบทพีทาโกรัส
1.2 บทกลับของทฤษฎีบทพีทาโกรัส
ทฤษฎีบทพีทาโกรัส คือ ทฤษฎีที่ว่าด้วยความสัมพันธ์ระหว่างด้านทั้งสามของรูปสามเหลี่ยมมุมฉาก
ซึ่งมีนิยามว่า “ในสามเหลี่ยมมุมฉากใด ๆ พื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านตรงข้ามมุมฉาก เท่ากับผลรวมพื้นที่ของสี่เหลี่ยมจัตุรัสที่มีด้านเป็นด้านประชิดมุมฉากของสามเหลี่ยมมุมฉากนั้น”
จากรูปด้านบนน้องจะเห็นว่า พี่มีสามเหลี่ยมมุมฉากอยู่ 1 อันประกอบไปด้วยด้าน 3 ด้านได้แก่ a,b,c ซึ่งโดยปกติแล้ว เรานิยมแทน c เป็นด้านตรงข้ามมุมฉาก (ด้านที่ยาวสุดของสามเหลี่ยม) ส่วนด้าน a,b เนื่องจากมันติดกับมุมฉากเลย เราจึงเรียกสองด้านนี่ว่า ด้านประกอบมุมฉาก
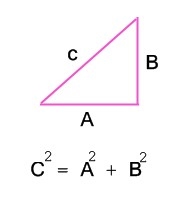
พีทาโกรัสกล่าวว่า ”ผลรวมของ(ด้านประกอบมุมฉากกำลังสอง) = ด้านตรงข้ามมุมฉากกำลังสอง” ซึ่งจากภาพด้านบนก็คือ a2+b2=c2 สมการนี้สมการเดียวเลยน้องที่ต้องจำ! เราเรียกมันว่า สูตรพีทาโกรัส
ตัวอย่างการใช้สมการทฤษฎีบทพีทาโกรัส
ทฤษฎีบทดังกล่าวสามารถเขียนเป็นสมการสัมพันธ์กับความยาวของด้าน a,b และ c ได้ ซึ่งมักเรียกว่า สมการพีทาโกรัส ซึ่งเขียนเป็นสมการได้ดังนี้
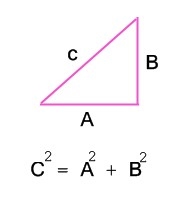
( อาจเขียนแทนด้วยตัวแปลอื่น เช่น x,y,z )






