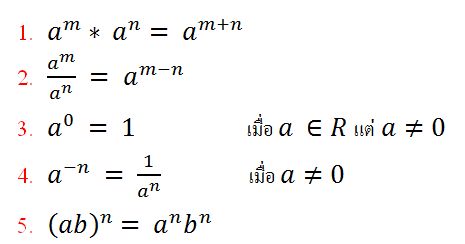เนื้อหาคณิต ม.1 เรื่องจำนวนเต็ม การสร้างทางเรขาคณิต เลขยกกำลัง

เนื้อหาคณิต ม.1 เทอม 1 ประกอบด้วย

จำนวนเต็ม
การสร้างทางเรขาคณิต
เลขยกกำลัง
ทศนิยมและเศษส่วน
รูปเรขาคณิตสองมิติและสามมิติ

จำนวนเต็ม (Integer)
จำนวนเต็ม คือ จำนวนที่ไม่มีเศษส่วนและทศนิยมรวมอยู่ในจำนวนนั้น
จำนวนเต็มประกอบด้วย
1. จำนวนเต็มบวก ได้แก่ 1 , 2 , 3 , 4 , 5 , 6 , …
2. จำนวนเต็มลบ ได้แก่ … , -4 , -3 , -2 , -1
3. ศูนย์ ได้แก่ 0

เรื่องจำนวนเต็ม

จำนวนเต็มบวก หรือ จำนวนนับ
จำนวนเต็มบวก หรือ จำนวนนับ คือ จำนวนเต็มที่มีค่ามากกว่า 0 ไปเรื่อย ๆโดยที่ไม่สามารถระบุได้
ว่าจำนวนนับตัวสุดท้ายเป็นอะไร จำนวนนับเริ่มต้นที่ 1 , 2 , 3, … ซึ่งเราทราบแล้วว่า จำนวนนับที่น้อยที่สุด คือ 1 จำนวน
นับที่มากที่สุดหาไม่ได้ คุณสมบัติของศูนย์และหนึ่ง

จำนวนเต็มลบ

จำนวนเต็มลบ คือ จำนวนที่มีค่าน้อยกว่า ศูนย์ มีตำแหน่งอยู่ทางด้านซ้ายมือของศูนย์เมื่ออยู่บนเส้นจำนวน
และ จะมีค่าลดลงเรื่อย ๆ โดยไม่สามารถจะบอกได้ว่าจำนวนใดจะมีค่าน้อยที่สุด แต่เราสามารถรู้ได้ว่าจำนวนเต็มลบ
ที่มีค่ามากที่สุด คือ -1 เราพอจะสรุปลักษณะที่สำคัญของจำนวนเต็มลบได้ดังนี้
1. จำนวนเต็มลบเป็นจำนวนที่มีค่าน้อยกว่าศูนย์ หรือถ้ามองบนเส้นจำนวนก็คือ เป็นจำนวนที่อยู่ทางซ้ายมือของศูนย์
2. จำนวนเต็มลบที่มีน้อยที่สุดไม่สามารถหาได้ แต่ จำนวนเต็มลบที่มีค่ามากที่สุด คือ -1
3. ตัวเลขที่ตามหลังเครื่องหมายลบ ถ้ายิ่งมีค่ามากขึ้นจำนวนเต็มลบนั้นจะมีค่าน้อยลงกล่าวคือ …-5 < -4 < -3 < -2 < -1

ศูนย์ ( ใช้สัญลักษณ์ “0” )

ศูนย์ ( ใช้สัญลักษณ์ “0” ) เป็นจำนวนเต็มอีกชนิดหนึ่ง ที่เราไม่ถือว่าเป็นจำนวนนับจากหลักฐานที่ค้นพบทำให้เราทราบ
ว่ามนุษย์รู้จักใช้สัญลักษณ์ “0” ในราวปีค.ศ. 800 โดยที่ “0” แทนปริมาณของการไม่มีของหรือของที่ต้องการกล่าวถึงแต่ก็ไม่ใช่ว่า 0
จะไม่มีความหมายถึงการไม่มีเสมอไป ตัวอย่างเช่น ระดับผลการเรียนทางด้านความรู้ โดยนักเรียนที่มีระดับผลการเรียนเป็น 0
ไม่ได้หมายความว่านักเรียนคนนั้นไม่มีความรู้ เพียงแต่ ว่ามีความรู้ในระดับหนึ่งเท่านั้น

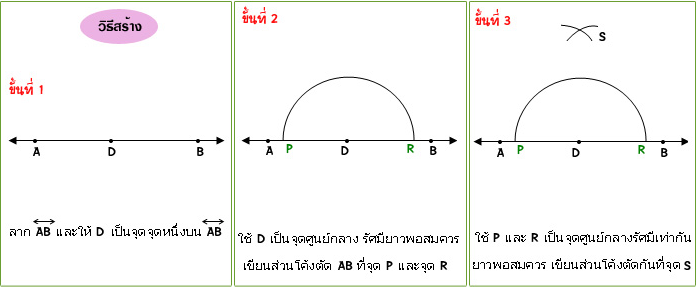
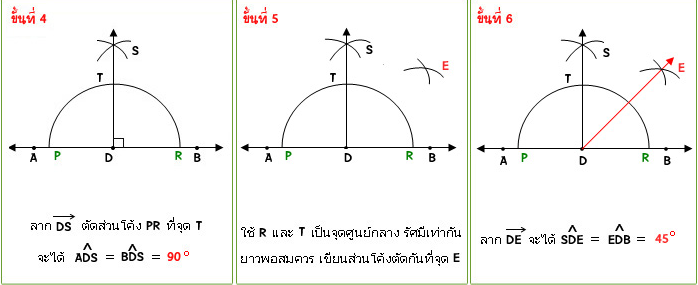
เรื่องการสร้างทางเรขาคณิต

เนื้อหาในบท การสร้างทางเรขาคณิต ที่ได้รวบรวมเนื้อหาไว้นั้น เป็นเพียงสูตรที่ใช้แก้ปัญหาในโจทย์ แต่การท่องจำสูตรเพียงอย่างเดียวอาจจะไม่พอ น้อง ๆจำเป็นต้องทำความเข้าใจและฝึกฝนในการทำโจทย์ทั้งเรื่อง จุด เส้นตรง และมุมต่างๆ ทั้งมุมแหลม มุมป้าน มุมฉาก และอื่นๆ เพื่อสร้างประสบการณ์ในการทำโจทย์ด้วย จึงจะทำให้มีความเข้าใจเรื่อง การสร้างเรขาคณิต มากยิ่งขึ้น

การสร้างมุมที่มีขนาด 90 องศา และ 45 องศา

การสร้างมุมที่มัขนาดเท่ากับ 90องศา อาศัยการสร้างเส้นตั้งฉาก ที่จุดจุดหนึ่งบนเส้นตรงที่กำหนดให้ ซึ่งจะใช้มุมฉาก และการสร้างมุมที่มีขนาด 45 องศา อาศัยการแบ่งครึ่งมุมฉากดังนี้