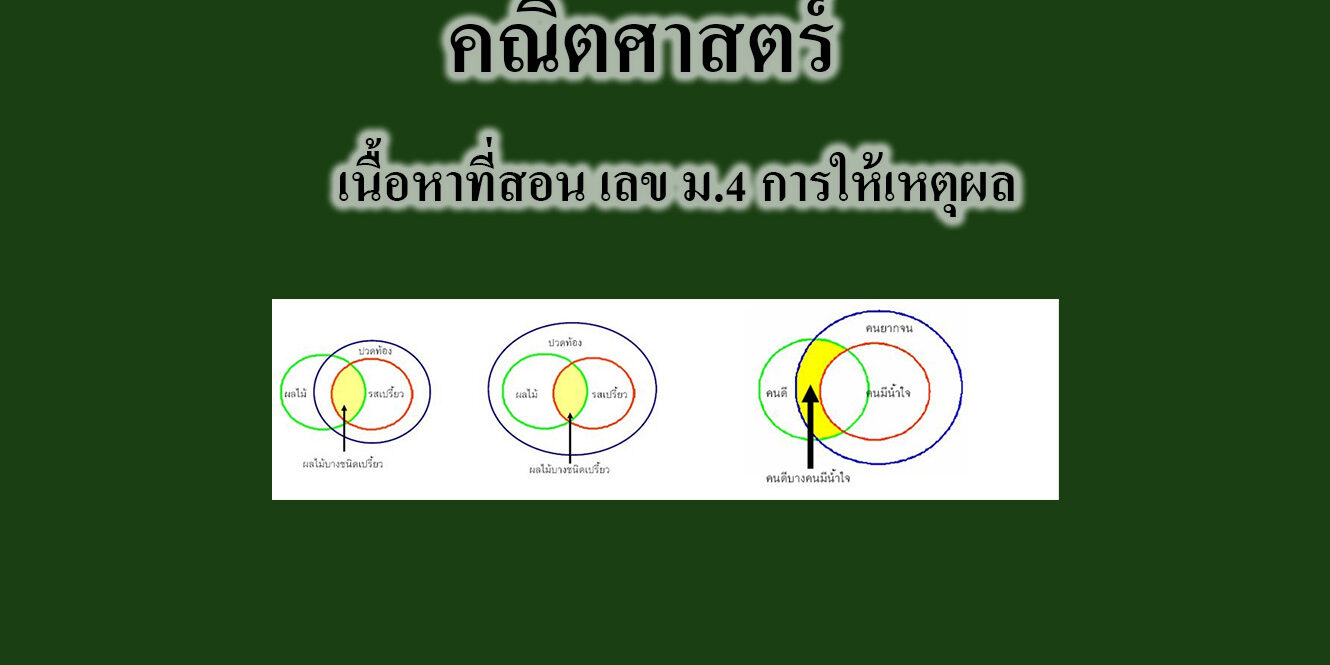
เนื้อหาที่สอน เลข ม.4 การให้เหตุผล

 เนื้อหาที่สอน เลข ม.4 การให้เหตุผล

(1) การให้เหตุผลแบบอุปนัย

(2) การให้เหตุผลแบบนิรนัย

การให้เหตุผล

การให้เหตุผลแบ่งได้ 2 แบบดังนี้
1. การให้เหตุผลแบบอุปนัย
2. การให้เหตุผลแบบนิรนัย

1. การให้เหตุผลแบบอุปนัย

การให้เหตุผลแบบอุปนัย  เป็นการให้เหตุผลโดยอาศัยข้อสังเกตหรือผลการทดลองจากหลาย ๆ ตัวอย่าง มาสรุปเป็นข้อตกลง หรือข้อคาดเดาทั่วไป  หรือคำพยากรณ์ ซึ่งจะเห็นว่าการจะนำเอาข้อสังเกต   หรือผลการทดลองจากบางหน่วยมาสนับสนุนให้ได้ข้อตกลง หรือ ข้อความทั่วไปซึ่งกินความถึงทุกหน่วย ย่อมไม่สมเหตุสมผล  เพราะเป็นการอนุมานเกินสิ่งที่กำหนดให้ ซึ่งหมายความว่า  การให้เหตุผลแบบอุปนัยจะต้องมีกฎของความสมเหตุสมผลเฉพาะของตนเอง  นั่นคือ  จะต้องมีข้อสังเกต หรือผลการทดลอง หรือ มีประสบการณ์ที่มากมายพอที่จะปักใจเชื่อได้  แต่ก็ยังไม่สามารถแน่ใจในผลสรุปได้เต็มที่ เหมือนกับการให้เหตุผลแบบนิรนัย  ดังนั้นจึงกล่าวได้ว่าการให้เหตุผลแบบนิรนัยจะให้ความแน่นอน แต่การให้เหตุผลแบบอุปนัย  จะให้ความน่าจะเป็น

ตัวอย่างการให้เหตุผลแบบอุปนัย  เช่น  เราเคยเห็นว่ามีปลาจำนวนมากที่ออกลูกเป็นไข่เราจึงอนุมานว่า “ปลาทุกชนิดออกลูกเป็นไข่”  ซึ่งกรณีนี้ถือว่าไม่สมเหตุสมผล  ทั้งนี้เพราะ ข้อสังเกต  หรือ  ตัวอย่างที่พบยังไม่มากพอที่จะสรุป  เพราะโดยข้อเท็จจริงแล้วมีปลาบางชนิดที่ออกลูกเป็นตัว  เช่น  ปลาหางนกยูง เป็นต้น

โดยทั่วไปการให้เหตุผลแบบอุปนัยนี้  มักนิยมใช้ในการศึกษาค้นคว้าคุณสมบัติต่าง ๆ ทางด้านวิทยาศาสตร์  เช่น ข้อสรุปที่ว่า  สารสกัดจากสะเดาสามารถใช้เป็นยากำจัดศัตรูพืชได้ ซึ่งข้อสรุปดังกล่าวมาจากการทำการทดลอง ซ้ำ ๆ กันหลาย ๆ ครั้ง  แล้วได้ผลการทดลองที่ตรงกันหรือในทางคณิตศาสตร์จะใช้การให้เหตุผลแบบอุปนัย  ในการสร้างสัจพจน์ เช่น  เมื่อเราทดลองลากเส้นตรงสองเส้นให้ตัดกัน  เราก็พบว่าเส้นตรงสองเส้นจะตัดกันเพียงจุด ๆ เดียวเท่านั้น  ไม่ว่าจะทดลองลากกี่ครั้งก็ตาม  เราก็อนุมานว่า    “เส้นตรงสองเส้นตัดกันเพียงจุด ๆ เดียวเท่านั้น”

ตัวอย่าง 1.

เมื่อเรามองไปที่ห่านกลุ่มหนึ่งพบว่า
ห่านตัวนี้สีขาว
ห่านตัวนั้นก็สีขาว
ห่านตัวโน้นก็สีขาว
ห่านนั้นก็สีขาว
ดังนั้น ห่านทุกตัวคงจะต้องมีสีขาว

ตัวอย่าง 2

ในการบวกเลข   2  จำนวน เราพบว่า
1+2  = 2+1
2+3  = 3+2
เราอาจสรุปได้ว่าทุกๆจำนวน a และ b  จะได้ว่า a + b = b + a

ตัวอย่าง 3

จากการสร้างรูปสามเหลี่ยมในระนาบ  พบว่า
เส้นมัธยฐานของสามเหลี่ยมรูป A พบกันที่จุดๆหนึ่ง
เส้นมัธยฐานของสามเหลี่ยมรูป B พบกันที่จุดๆหนึ่ง
เส้นมัธยฐานของสามเหลี่ยมรูป C พบกันที่จุดๆหนึ่ง
ดังนั้น เส้นมัธยฐานของสามเหลี่ยมใดๆ  พบกันที่จุดๆหนึ่งเสมอ

ข้อสังเกต

1.ข้อสรุปของการให้เหตุผลแบบอุปนัยอาจจะไม่จริงเสมอไป

2. การสรุปผลของการให้เหตุผลแบบอุปนัยอาจขึ้นอยู่กับประสบการณ์ของผู้สรุป

3. ข้อสรุปที่ได้จากการให้เหตุผลแบบอุปนัยไม่จำเป็นต้องเหมือนกัน

ตัวอย่าง   กำหนด จำนวน 2, 4, 6 , a จงหา จำนวน a  จะได้ a = 8
กำหนด จำนวน 2, 4, 6 , a จงหา จำนวน a
จะได้ a = 10  เพราะว่า 4 + 6  = 10
กำหนด จำนวน 2, 4, 6 , a จงหา จำนวน a  จะได้ a = 22
เพราะว่า 6 = (2 x 4)-2 และ 22 = (4 x 6)-2

4. ข้อสรุปของการให้เหตุผลแบบอุปนัยอาจ ผิดพลาดได้

ตัวอย่าง ให้ F(n) = n² – 79n + 1601

ทดลองแทนค่าจำนวนนับ n ใน F(n)
n = 1 ได้  F(1) = 1523 เป็นจำนวนเฉพาะ
n = 2 ได้  F(2) = 1447 เป็นจำนวนเฉพาะ
n = 3 ได้  F(3) = 1373 เป็นจำนวนเฉพาะ

F(n) = n² – 79n + 1601

แทนค่า n ไปเรื่อยๆ จนกระทั่งแทน n = 79  ได้ F(79)  เป็นจำนวนเฉพาะ

จากการทดลองดังกล่าว   อาจสรุปได้ว่า  n² – 79n + 1601 เป็นจำนวนเฉพาะ สำหรับทุกจำนวนนับ   แต่…
F(n)   = n² – 79n + 1601
F(80) = 80² – (79)(80) + 1601
=  1681
=   (41)(41)

F(80) ไม่เป็นจำนวนเฉพาะ

2. การให้เหตุผลแบบนิรนัย

เป็นการนำความรู้พื้นฐานที่อาจเป็นความเชื่อ ข้อตกลง กฏ หรือบทนิยาม  ซึ่งเป็นสิ่งที่รู้มาก่อนและยอมรับว่าเป็นจริง เพื่อหาเหตุผลนำไปสู่ข้อสรุป

ตัวอย่าง 1

มนุษย์ทุกคนเป็นสิ่งมีชีวิต และ นายแดงเป็นมนุษย์คนหนึ่ง
เพราะฉะนั้น นายแดงจะต้องเป็นสิ่งมีชีวิต

ตัวอย่าง 2

ปลาโลมาทุกตัวเป็นสัตว์เลี้ยงลูกด้วยนม  และสัตว์เลี้ยงลูกด้วย
นม ทุกตัวมีปอด
ดังนั้น ปลาโลมาทุกตัวมีปอด

ตัวอย่าง 3

แมงมุมทุกตัวมี 6 ขา  และสัตว์ที่มี 6 ขา ทุกตัวมีปีก
ดังนั้น แมงมุมทุกตัวมีปีก

การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบนิรนัยเป็นวิธีการให้เหตุผลโดยสรุปผลจากข้อความซึ่งเป็นความจริงทั่วไปมาเป็นข้ออ้างเพื่อสนับสนุนให้เกิดข้อสรุปที่เป็นความรู้ใหม่ที่เป็นข้อสรุปส่วนย่อยข้อสรุปที่ได้จากการให้เหตุผล

แบบนิรนัยนั้นจะเป็นข้อสรุปที่อยู่ในขอบเขตของเหตุเท่านั้นจะเป็นข้อสรุปที่กว้างหรือเกินกว่าเหตุไม่ได้การให้เหตุผลแบบนิรนัยประกอบด้วยข้อความ2กลุ่มโดยข้อความกลุ่มแรกเป็นข้อความที่เป็นเหตุ เหตุอาจมี

หลาย ๆเหตุ หลาย ๆข้อความ และข้อความกลุ่มที่สองจะเป็นข้อสรุป ข้อความในกลุ่มแรกและกลุ่มที่สองจะต้องมีความสัมพันธ์กัน

ข้อจำกัดของการให้เหตุผลแบบนิรนัย

1.การให้เหตุผลแบบนิรนัยเป็นการให้เหตุผลที่มีขนาดใหญ่ซึ่งกำหนด เป็นการวางนัยทั่วไปและมีเหตุรองเป็น เหตุการณ์เฉพาะเพื่อนำไปสู่ข้อสรุป ดังนั้นเหตุจะเป็นข้อความหรือสมมุติฐานฐานใด ๆ ที่อาจเป็นจริงหรือไม่จริงในชีวิตประจำวันก็ได้ แต่ถ้าข้อความนั้นไม่จริงก็จะทำให้เกิดข้อเสียหายแก่ข้อสรุป เนื่องจากเหตุผลแบบนิรนัยจะสรุปผลในขอบเขตของเหตุที่กำหนดไว้เท่านั้น

2. การให้เหตุผลแบบนิรนัยไม่สามารถสรุปผลตามที่คาดหวังไว้ได้ต้องสรุปให้เป็นไปตามเหตุการณ์ต่าง ๆที่กำหนดไว้เท่านั้น ดังเช่น

 เหตุ  1. นกทุกชนิดบินได้

2. เพนกวิน เป็นนกชนิดหนึ่ง

ผลสรุป นกเพนกวินบินได้    

        3.เมื่อเราใช้วิธีการให้เหตุผลแบบนิรนัยเพียงอย่างเดียวจะทำให้วิทยาการต่าง ๆก้าวหน้าได้อย่างช้ามากหรือไม่ก้าวหน้าเลยเพราะว่าความรู้ทั่วไปที่จะมาเป็นการวางนัยทั่วไปจะใช้เวลาที่ยาวนานมากเพราะเป็นความรู้ที่ถูกต้องจากผู้รู้ในสมัยก่อนๆ ซึ่งมีอยู่ไม่มากนักการใช้ความรู้ที่มีอยู่แบบเดิมมาใช้โดยไม่ก่อให้เกิดความรู้ใหม่เพิ่มเติมนั้นจะเป็นผลให้ไม่เกิดความก้าวหน้าทางวิทยาการหรือก้าวหน้าได้อย่างช้ามาก

ตัวอย่างการให้เหตุผลแบบนิรนัย

ตัวอย่างที่ 1  เหตุ  1. สัตว์ทุกชนิดต้องตาย

2. มนุษย์เป็นสัตว์

3. ดำเป็นมนุษย์

ผลสรุป ดำต้องตาย

 ตัวอย่างที่ 2  เหตุ  1. จำนวนที่หารด้วย 2 ไม่ลงตัว เรียกว่า จำนวนคี่

2. X เป็นจำนวนที่หารด้วย 2 ลงตัว

ผลสรุป x ไม่เป็นจำนวนคี่

ตัวอย่างที่ 3  เหตุ  1. เด็กที่ขาดสารไอโอดีน ทุกคนเป็นโรคคอพอก

2. เด็กที่อยู่ในท้องถิ่นที่ห่างไกลจากทะเลทุกคนขาดสารไอโอดีน

3. หมู่บ้าน ก อยู่ห่างไกลจากทะเล

4. เด็กชายต้น อยู่ในหมู่บ้าน ก

                     ผลสรุป เด็กชายต้นเป็นโรคคอพอก

 ตัวอย่างที่ 4  เหตุ 1. รูปสามเหลี่ยมหน้าจั่วเป็นรูปสามเหลี่ยมที่มีมุมที่ฐานมีขนาดเท่ากัน 2 มุม

2. รูปสามเหลี่ยมมุมฉากเป็นรูปสามเหลี่ยมที่มีขนาดเท่ากัน 2 มุม

    ผลสรุป รูปสามเหลี่ยมมุมฉากเป็นรูปสามเหลี่ยมหน้าจั่ว

2. การให้เหตุผลแบบอุปนัย

 การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เกิดจากการที่มีสมมติฐานกรณีเฉพาะ หรือเหตุย่อยหลายๆ เหตุ เหตุย่อยแต่ละเหตุเป็นอิสระจากกัน มีความสำคัญเท่าๆ กัน และเหตุทั้งหลายเหล่านี้ไม่มีเหตุใดเหตุหนึ่งแสดงให้เห็นถึงความเป็นสมมติฐานกรณีทั่วไป หรือกล่าวได้ว่า การให้เหตุผลแบบอุปนัยคือการนำเหตุย่อยๆ แต่ละเหตุมารวมกัน เพื่อนำไปสู่ผลสรุปเป็นกรณีทั่วไป เช่นตัวอย่างการให้เหตุผลแบบอุปนัย

1. สุนทรี พบว่า ทุกครั้งที่คุณแม่ไปซื้อก๋วยเตี๋ยวผัดไทยจะมีต้นกุยช่ายมาด้วยทุกครั้ง  จึงสรุปว่า ก๋วยเตี๋ยวผัดไทยต้องมีต้นกุยช่าย

2.ชาวสวนมะม่วงสังเกตมาหลายปีพบว่า ถ้าปีใดมีหมอกมาก ปีนั้นจะได้ผลผลิตน้อย เขาจึงสรุปว่าหมอกเป็นสาเหตุที่ทำให้ผลผลิตน้อย ต่อมามีชาวสวนหลายคนทดลองฉีดน้ำล้างช่อมะม่วง เมื่อมีหมอกมากๆ พบว่าจะได้ผลผลิตมากขึ้นจึงสรุปว่า การล้างช่อมะม่วงตอนมีหมอกมากๆ จะทำให้ได้ผลผลิตมากขึ้น

         3.นายสมบัติ พบว่า ทุกครั้งที่ทำความดีจะมีความสบายใจ  จึงสรุปผลว่า การทำความดีจะทำให้เกิดความสบายใจ การให้เหตุผลแบบอุปนัย เป็นวิธีการให้เหตุผลโดยสรุปจากเหตุหลาย ๆ เหตุโดยถือหลักความจริงของเหตุจากส่วนย่อยหรือส่วนเฉพาะไปสู่การสรุปความจริงที่เป็นส่วนใหญ่ หรือส่วนร่วมโดยที่เหตุผลลักษณะนี้จะประกอบไปด้วย ข้อความ 2 กลุ่มคือ ข้อความที่เป็นส่วนของเหตุและข้อความที่เป็นข้อสรุป โดยกลุ่มของข้อความที่เป็นเหตุจะทำให้เกิดข้อสรุปของข้อความในกลุ่มหลังเราสามารถกล่าวได้ว่าการให้เหตุผลแบบอุปนัยมีลักษณะการนำความรู้ที่ได้จากการตัดสินใจจากประสบการณ์หลาย ๆครั้ง การสังเกต หรือการทดลองหลาย ๆ ครั้งมาเป็นเหตุย่อยหรือสมมติฐานต่าง ๆ แล้วนำมาสรุปเป็นคุณสมบัติของส่วนรวมทั้งหมดเป็นข้อความหรือความรู้ทั่วไปซึ่งจะครอบคลุมไปถึงสิ่งที่ยังไม่มีประสบการณ์หรือยังไม่ได้กล่าวอีกด้วย   

 ข้อจำกัดของการให้เหตุผลแบบอุปนัย