เรขาคณิตวิเคราะห์ คณิตศาสตร์ ม.4

 เรขาคณิตวิเคราะห์

3.1 ความรู้เบื้องต้นเกี่ยวกับเรขาคณิตวิเคราะห์

3.2 ภาคตัดกรวย (วงกลม วงรี พาราโบลา ไฮเพอร์โบลา การเลื่อนแกน)

 เรขาคณิตวิเคราะห์และภาคตัดกรวย

• ความชันของเส้นตรง (Slope : m)
• เส้นขนานและเส้นตั้งฉาก
• ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง
• ภาคตัดกรวย (conic section หรือ conic)
• วงกลม
• สมการวงกลม
• วงรี
• สมการวงรี
• พาราโบลา
• ไดเรกตริกซ์
• สมการพาราโบลา

• ความรู้เบื้องต้นเกี่ยวกับเรขาคณิตวิเคราะห์
  • ระยะทางระหว่างจุดสองจุด
  • จุดกึ่งกลางระหว่างจุดสองจุด
  • ความชันของเส้นตรง
  • เส้นขนาน
  • เส้นตั้งฉาก
  • ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง
  • ระยะห่างระหว่างเส้นตรงกับจุด
• ภาคตัดกรวย
  • วงกลม
  • วงรี
  • พาราโบลา (Parabola)
  • ไฮเพอร์โบลา (Hyperbola)
  • การเลื่อนกราฟ

เส้นตรง

เส้นตรง มีสมการรูปแบบทั่วไปคือ Ax + By + C = 0 และสมการรูปแบบมาตรฐานของเส้นตรงจะเขียนอยู่ในรูป y = mx + C ซึ่งจะอยู่ในหัวข้อ “สมการเส้นตรง” เส้นตรงหนึ่งเส้นประกอบไปด้วยจุดหลายจุด ซึ่งจุดเหล่านี้จะทำให้เราสามารถหาความชันได้ และเมื่อเราทราบความชันก็จะสามารถหาสมการเส้นตรงได้นั่นเอง

ความชันของเส้นตรง

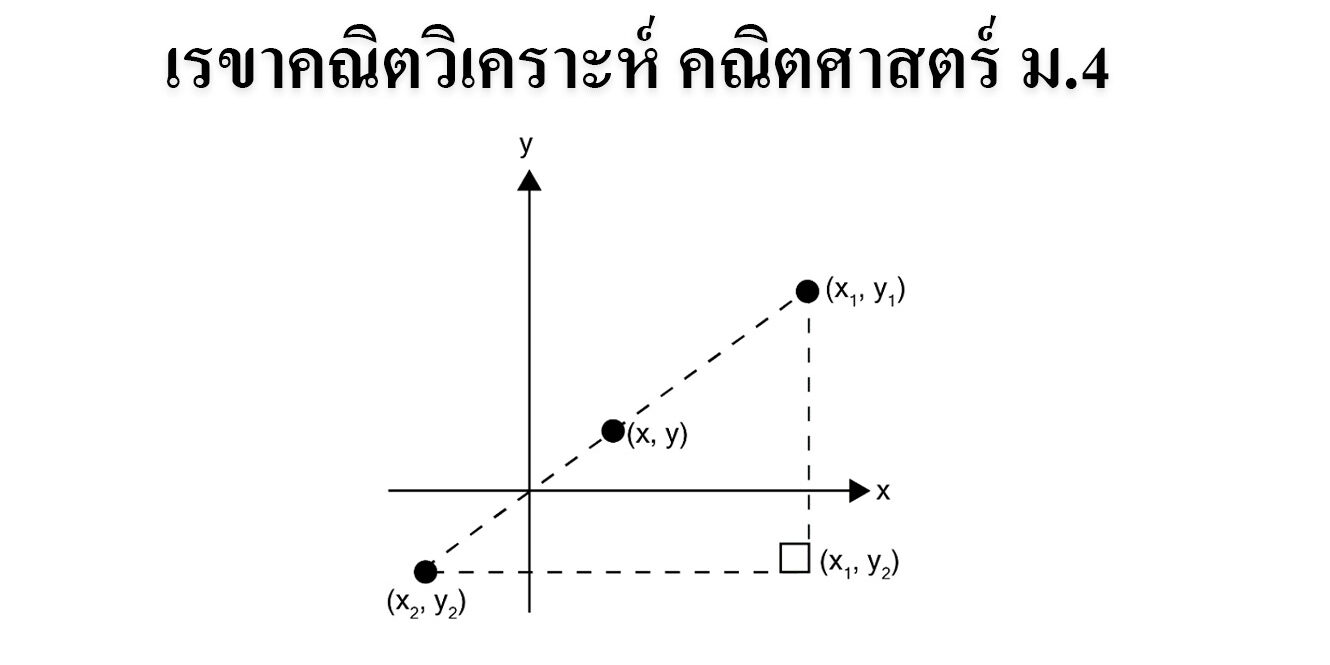
ความชันของเส้นตรง ส่วนใหญ่นิยมใช้ m แทนความชัน การหาความชันนั้นเราจะต้องรู้จุดบนเส้นตรงอย่างน้อย 2 จุด

สมมติ ให้สองจุดนั้นเป็น (x₁,y₁) และ (x₂,y₂)   เป็นจุดบนเส้นตรง L  ดังรูป

จะได้ว่า ความชันของเส้นตรง L หาได้จาก

ความชันของเส้นตรง (Slope : m)

m =  (y_{2  –}  y₁) / (x_{2  –}  x₁)

ความชันของเส้นตรง (Slope : m)

คือ อัตราส่วนระหว่างค่า y ที่เปลี่ยนแปลงไป ต่อค่า x ที่เปลี่ยนแปลงไป ใช้ สัญลักษณ์ m โดยค่า m อาจะเป็นบวก หรือลบ หรือเป็นศูนย์ก็ได้

• ถ้า m>0 แสดงว่า เส้นตรงนี้เฉียงขึ้นทางขวา
• ถ้า m<0 แสดงว่า เส้นตรงนี้เฉียงลงทางขวา
• ถ้า m=0 แสดงว่า เป็นเส้นนอนขนานแกน x
• ส่วนเส้นตั้งขนานกับแกน y นั้น m หาค่าไม่ได้ (เป็นอนันต์)

ภาคตัดกรวย (Conic Section)

วงกลม และ วงรี คือ เส้นโค้งซึ่งได้จากการตัดกรวย ด้วยระนาบ ให้ได้เส้นโค้งปิด (เป็นวง) วงกลมนั้นถือเป็นกรณีพิเศษของวงรี โดยแนวของระนาบในการตัดนั้น ตั้งฉากกับแกนกลางของกรวย หากระนาบตัดกรวยในแนวขนานกับเส้นขอบของกรวย หรือเรียก เส้นกำเนิดกรวย (generator line) จะได้เส้นโค้งเรียกว่า พาราโบลา หากระนาบไม่อยู่ในแนวขนานเส้นขอบ และตัดกรวยได้เส้นโค้งเปิดไม่เป็นวง จะเรียกเส้นโค้งนี้ว่า ไฮเพอร์โบลา จะเห็นได้ว่าในกรณีนี้ระนาบจะตัดกรวยทั้งครึ่งบน และครึ่งล่าง ได้เป็นเส้นโค้งที่ขาดจากกันสองเส้น

ในกรณีที่เรียกว่าในภาษาอังกฤษว่า ดีเจนเนอเรต ระนาบจะตัดผ่านจุดยอดของกรวย และได้ผลของการตัดเป็น จุด เส้นตรง หรือ เส้นตรงสองเส้นตัดกัน กรณีเหล่านี้ไม่ได้ถูกรวมไว้ในภาคตัดกรวย

เส้นโค้งที่เกิดจาการตัดกรวย ประกอบด้วย

• วงกลม (Circle)
• วงรี (Ellipse)
• พาราโบลา (Parabola)
• ไฮเพอร์โบลา (Hyperbola)1. หากระนาบขนานไปกับฐานกรวย ขอบหน้าตัดจะเป็นรูปวงกลม
  2. หากระนาบเอียง แต่ยังไม่เอียงจนตัดไปถึงฐานกรวย ขอบหน้าตัดจะเป็นรูปวงรี
  3.หากระนาบเอียงจนตัดฐานกรวยหนึ่ง ขอบหน้าตัดจะเป็นโค้งที่มีชื่อว่า พาราโบลา
  4.หากระนาบเอียงจนไปตัดกรวยอีกฟาก ขอบหน้าตัดจะเกิดเป็นโค้งที่มีชื่อว่า ไฮเปอร์โบลา

กราฟและสมการของภาคตัดกรวยแต่ละชนิด โดยอาศัยหลักการเลื่อนกราฟ ได้ดังตารางต่อไปนี้

ภาคตัดกรวย	กราฟ	สมการรูปแบบมาตรฐานและข้อเท็จจริงที่สำคัญ
วงกลม		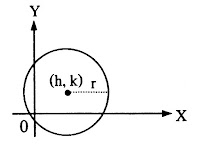สมการ จุดศูนย์กลาง (h, k) รัศมียาว r หน่วย
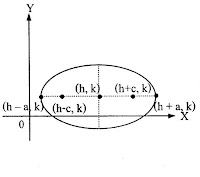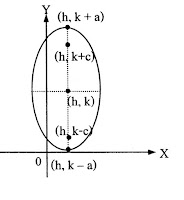
วงรี		สมการ แกนเอกอยู่ในแนวนอน จุดศูนย์กลาง (h, k) จุดยอด (h-a, k), (h+a, k) โฟกัส (h-c, k), (h+c, k); c2= a2 – b2 แกนเอกยาว 2a หน่วย แกนโทยาว 2b หน่วย
		สมการ แกนเอกอยู่ในแนวตั้ง จุดศูนย์กลาง (h, k) จุดยอด (h, k-a), (h, k+a) โฟกัส (h, k-c), (h, k+c); c2= a2 – b2 แกนเอกยาว 2a หน่วย แกนโทยาว 2b หน่วย
พาราโบลา		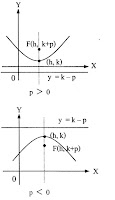สมการ แกนสมมาตรอยู่ในแนวตั้ง จุดยอด (h, k) โฟกัส (h, k+p) P > 0 เส้นโค้งหงายขึ้น P < 0 เส้นโค้งคว่ำลง ไดเรกตริกซ์ y = k – p
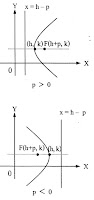		สมการ แกนสมมาตรอยู่ในแนวตั้ง จุดยอด (h, k) โฟกัส (h+p, k) P > 0 เส้นโค้งเปิดด้านขวา P < 0 เส้นโค้งเปิดด้านซ้าย ไดเรกตริกซ์ x = h – p
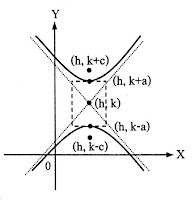
ไฮเพอร์โบลา		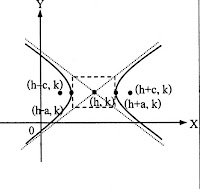สมการ แกนตามขวางอยู่ในแนวนอน จุดศูนย์กลาง (h, k) จุดยอด (h-a, k), (h+a, k) โฟกัส (h-c, k), (h+c, k); c2= a2 + b2 แกนตามขวางยาว 2a หน่วย แกนสังยุคยาว 2b หน่วย
		สมการ แกนเอกอยู่ในแนวตั้ง จุดศูนย์กลาง (h, k) จุดยอด (h, k-a), (h, k+a) โฟกัส (h, k-c), (h, k+c); c2= a2 + b2 แกนตามขวางยาว 2a หน่วย แกนสังยุคยาว 2b หน่วย

สมการทั่วไปของภาคตัดกรวย

    กราฟของสมการ  เมื่อ A และ C ไม่เป็นศูนย์พร้อมกันเป็นภาคตัดกรวยหรือภาคตัดกรวยลดรูป ในกรณีที่ไม่ใช่ภาคตัดกรวยลดรูป กราฟของสมการเป็น

1. วงกลม        ถ้า  A = C
2. วงรี          ถ้า   AC > 0
3. พาราโบลา     ถ้า   AC = 0
4. ไฮเพอร์โบลา    ถ้า  AC < 0

กำเนิดภาคตัดกรวย

ภาคตัดกรวย (conic section) เป็นเนื้อหาแขนงหนึ่งจากเรื่องเรขาคณิตวิเคราะห์ในวิชาคณิตศาสตร์ที่ได้รับบรรจุให้อยู่ในเนื้อหาคณิตศาสตร์ ม.4 ภาคตัดกรวยหมายถึง เส้นโค้งที่ได้จากการตัดพื้นผิวกรวยกลม ด้วยระนาบแบน ภาคตัดกรวยนี้ถูกตั้งเป็นหัวข้อศึกษาตั้งแต่สมัย 200 ปีก่อนคริสต์ศักราชโดย อะพอลโลเนียสแห่งเพอร์กา (Apollonius of Perga) ผู้ที่มีชีวิตอยู่ในช่วง 262 – 190 ปีก่อนคริสต์ศักราช ผู้ซึ่งศึกษาภาคตัดกรวยและค้นพบสมบัติหลายประการของภาคตัดกรวย พบว่าภาคตัดกรวยไม่เพียงแต่เป็นเส้นโค้งที่สวยงามแต่นำไปใช้ประโยชน์ได้หลายด้าน ต่อมากรณีการศึกษาภาคตัดกรวยถูกนำไปใช้ประโยชน์หลายแบบ ได้แก่

กาลิเลโอ กาลิเลอี

• ค.ศ.1590 กาลิเลโอ (Galileo Galile) พบว่าขีปนาวุธที่ยิงขึ้นไปในมุมที่กำหนดมีวิถีการเคลื่อนที่เป็นพาราโบลา
• ค.ศ.1609 เคปเลอร์ (Kapler) พบว่าวงโคจรของดาวเคราะห์รอบดวงอาทิตย์เป็นวงรี
• ค.ศ.1668 ไอแซค นิวตัน (Isaac Newton) เป็นบุคคลแรกที่ประดิษฐ์กล้องโทรทรรศน์ชนิดสะท้อนแสงโดยอาศัยหลักการที่มีพื้นฐานจากสมบัติของพาราโบลาและไฮเพอร์โบลา ในปัจจุบันมีการศึกษาเกี่ยวกับการนำสมบัติของภาคตัดกรวยไปใช้ประโยชน์ในด้านต่างๆ เพิ่มเติมตลอดเวลา เช่น ใช้จานทรงพาราโบลา (รูปเรขาคณิตสามมิติที่เกิดจากการหมุนพาราโบลารอบแกนสมมาตรของพาราโบลา) เป็นอุปกรณ์เก็บรวบรวมสัญญาณ เช่น จานรับส่งสัญญาณในระบบโทรคมนาคม หรือใช้เป็นอุปกรณ์เก็บพลังงานจากดวงอาทิตย์ หรือใช้เป็นอุปกรณ์สำหรับสะท้อนแสง เช่น โคมไฟ การหาตำแหน่งของเรือในทะเลโดยใช้จุดตัดของไฮเพอร์โบลา การทำงานของอุปกรณ์ที่ใช้สลายก้อนนิ่วในไตใช้สมบัติการสะท้อนของวงรี

สมการวงกลม

วงกลม คือเซตของจุดทุกจุดซึ่งห่างจากจุดคงที่จุดหนึ่งเป็นระยะทางคงตัว จุดคงที่ เรียกว่า จุดศูนย์กลาง ส่วนระยะคงที่เรียกว่า รัศมี

นิยามของสมการวงกลมคือ

วงกลม (circle) คือเซตของจุดทั้งหมดในระนาบที่ห่างจากจุดๆหนึ่งตรึงอยู่กับที่เป็นระยะทางคงตัว จุดที่ตรึงอยู่กับที่นี้เรียกว่า จุดศูนย์กลาง (center) ของวงกลม และระยะทางคงตัวดังกล่าวเรียกว่า รัศมี (radius) ของวงกลม

นิยามของสมการพาราโบลา

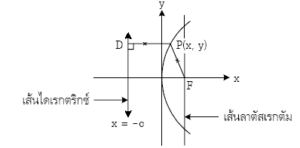
พาราโบลา คือเซตของจุดบนพื้นระนาบซึ่งมีระยะห่างจากจุดคงที่ เท่ากับระยะที่ห่างจากเส้นคงที่

จุดคงที่ คือจุดโฟกัส (Focus)

เส้นตรงที่คงที่ คือเส้นไดเรกตริกซ์ (Directrix)

เส้นลาตัสเลกตัม (Latus Rectum) คือเส้นตรงที่ลากผ่านจุดโฟกัสและตั้งฉากกับแกนของรูป

แกนของรูปหรือแกนสมมาตร คือเส้นตรงที่ลากผ่านจุดยอดและผ่านจุดโฟกัส

คอร์ดของพาราโบลา คือเส้นตรงที่ลากเชื่อมจุด 2 จุด ที่ต่างกันของพาราโบลาและคอร์ดที่ลากผ่านจุดโฟกัสเรียกว่า Focul ส่วนคอร์ดที่ลากผ่านจุดโฟกัสด้วย และตั้งฉากกับแกนของรูปด้วย เรียกว่า ลาตัสเรกตัม (Latus Recrum)

นิยามสมการวงรี

วงรี (Ellipse) คือเซตของจุดทั้งหมดในระนาบซึ่งผลบวกของระยะทางจากจุดใดๆจุดหนึ่งในเซตไปยังจุดคงที่ 2 จุดมีค่าคงตัว

 

จากบทนิยามนี้ มีวิธีง่ายๆ ในการวาดรูปวงรี (ดูรูปที่ 2) วางกระดาษบนกระดานวาดรูปปักหมุด 2 ตัวที่จุดต่างกัน ใช้เป็นโฟกัสของวงรี ตัดเชือกเส้นหนึ่งยาวกว่าระยะทางระหว่างหมุดทั้งสอง ผูกปลายเชือกแต่ละข้างกับหมุด โดยใช้ดินสอรั้งเชื่อให้ตึงตลอดเวลา ขณะที่ค่อยๆ เคลื่อนดินสอรอบโฟกัส รอยดินสอที่เกิดขึ้นจะเป็นรูปวงรีเพราะผลบวกของระยะทางจากจุดปลายดินสอถึงโฟกัสทั้งสองเท่ากับความยาวของเชือกที่มีความยาวคงตัวเสมอ

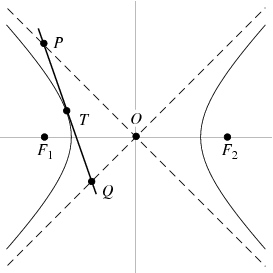
นิยามของสมการไฮเพอร์โบลา

ไฮเพอร์โบลา (Hyperbola) คือเซตของจุดทั้งหมดในระนาบซึ่งผลต่างของระยะทางจากจุดใดๆไปยังจุด F1 และ F2 ที่ตรึงอยู่กับที่มีค่าคงตัว โดยค่าคงตัวน้อยกว่าระยะห่างระหว่างจุดคงที่ที่ตรึงอยู่กับที่ทั้งสอง จุด F1 และ F2 ดังกล่าวนี้เรียกว่า โฟกัส (Focus) ของไฮเพอร์โบลา