เรียนคณิตศาสตร์ ม.5 คณิตศาสตร์พื้นฐานเรื่อง ฟังก์ชัน

บทที่ 2 ฟังก์ชัน

2.1 ฟังก์ชัน

2.2 ฟังก์ชันเชิงเส้น

2.3 ฟังก์ชันกำลังสอง

2.4 ฟังก์ชันขั้นบันได

2.5 ฟังก์ชันเอกซ์โพเนนเชียล

ฟังก์ชันเชิงเส้นและฟังก์ชันกำลังสอง-ฟังก์ชัน ม.4

ฟังก์ชันเชิงเส้นและฟังก์ชันกำลังสอง

ฟังก์ชันเชิงเส้น

ฟังก์ชันเชิงเส้น คือ ฟังก์ชันที่อยู่ในรูป y = ax + b เมื่อ a และ b เป็นจำนวนจริง โดยที่ a 0

กราฟของฟังก์ชันเชิงเส้นจะเป็นเส้นตรง

วิธีวาดกราฟฟังก์ชันเชิงเส้น

ขั้นที่ 1 หาจุดตัดก่อน

หาจุดตัดแกน x ให้ค่า y = 0
หาจุดตัดแกน y ให้ค่า x = 0

ขั้นที่ 2 ลากเส้นเชื่อมระหว่างจุด

ฟังก์ชันกำลังสอง

ฟังก์ชันกำลังสอง คือ ฟังก์ชันที่อยู่ในรูป y = ax2 + bx + c เมื่อ a , b และ c เป็นจำนวนจริง โดยที่ a 0
กราฟของฟังก์ชันกำลังสองจะเป็นรูปพาราโบลา

รูปแบบฟังก์ชันกำลังสอง
1. รูปแบบมาตรฐาน y = a(x – h)² + k
จุดยอดอยู่ที่ (h , k)
สมการแกนสมมาตร x = h

อย่าลืม. ถ้า a > 0 กราฟหงาย
a < 0 กราฟคว่ำ

2. รูปแบบทั่วไป y = ax² + bx + c

จุดยอดอยู่ที่ . ่

สมการแกนสมมาตร x =

อย่าลืม ถ้า a > 0 กราฟหงาย
a < 0 กราฟคว่ำ

ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได (Step Function)

ฟังก์ชันขั้นบันได หมายถึงฟังก์ชันที่มีโดเมนเป็นสับเซตของเซตของจำนวนจริงและมีค่าของฟังก์ชันเป็นค่าคงตัวเป็นช่วงๆ

มากกว่าสองช่วงกราฟของฟังก์ชันนี้มีลักษณะคล้ายขั้น บันได

กราฟของฟังก์ชันนี้จะมีรูปร่างคล้ายขั้นบันได

นิยาม

ฟังก์ชัน f : R → R จะเรียกว่าฟังก์ชันขั้นบันได ถ้าฟังก์ชัน fสามารถเขียนให้อยู่ในรูปแบบนี้ได้

สำหรับทุกจำนวนจริง x

เมื่อ n ≥ 0, α_i เป็นจำนวนจริง (ค่าคงตัว), A_i คือช่วงต่าง ๆ และ χ_A คือฟังก์ชันบ่งชี้

(indicator function) ของช่วง Aนั่นคือ

ในนิยามเช่นนี้ ช่วง A_i ต่าง ๆ จะต้องมีสมบัติที่สมมติขึ้นสองประการดังนี้

ช่วงต่าง ๆ จะต้องไม่มีส่วนร่วมต่อกัน นั่นคือ A_i ∩ A_j = ∅ โดยที่ i ≠ j
ยูเนียนของช่วงทุกช่วง คือเซตจำนวนจริงทั้งเซต นั่นคือ ∪_i A_i = R

ในกรณีที่สมบัติของฟังก์ชันเริ่มต้นไม่เป็นไปตามข้อสันนิษฐาน เช่นช่วงซ้อนกัน หรือยูเนียนแล้วแต่ไม่ครบเซต

จำนวนจริง เราอาจเลือกช่วงใหม่ที่เทียบเท่าอันทำให้มีสมบัติดังกล่าวได้ ตัวอย่างเช่น กำหนดให้ฟังก์ชันขั้นบันไดนี้

สามารถเขียนใหม่ได้เป็น

สมบัติ

ผลรวมและผลคูณของฟังก์ชันขั้นบันไดสองฟังก์ชัน จะให้ผลเป็นฟังก์ชันขั้นบันไดอีกฟังก์ชันหนึ่ง

และผลคูณของฟังก์ชันขั้นบันไดกับจำนวนคงตัวก็ยังคงเป็นฟังก์ชันขั้นบันได จากกรณีทั้งสองทำให้

ฟังก์ชันขั้นบันไดก่อร่างพีชคณิตขึ้นมาเหนือจำนวนจริง
ฟังก์ชันขั้นบันไดมีจำนวนช่วงเป็นจำนวนจำกัดเท่านั้น ถ้าช่วง A_i ต่าง ๆ

ซึ่ง i = 0, 1, …, n ตามนิยามข้างต้นไม่ทับซ้อนซึ่งกันและกัน และยูเนียนของช่วงทั้งหมดเป็นจำนวนจริง

จะได้ว่า f (x) = α_i สำหรับทุกค่าของ x ∈ A_i
ปริพันธ์เลอเบกของฟังก์ชันขั้นบันได คือ

เมื่อ คือความยาวของช่วง A และในกรณีนี้เราสมมติว่าช่วง A_i ทั้งหมดมีความยาวจำกัด

ข้อเท็จจริงคือความเท่ากันนี้สามารถใช้เป็นขั้นตอนแรกในการหาปริพันธ์เลอเบก ^[1]

สมบัติ

และผลคูณของฟังก์ชันขั้นบันไดกับจำนวนคงตัวก็ยังคงเป็นฟังก์ชันขั้นบันได จากกรณีทั้งสองทำให้ฟังก์ชันขั้นบันไดก่อร่าง

พีชคณิตขึ้นมาเหนือจำนวนจริงฟังก์ชันขั้นบันไดมีจำนวนช่วงเป็นจำนวนจำกัดเท่านั้น ถ้าช่วง A_i ต่าง ๆ ซึ่ง i = 0, 1, …, n

ตามนิยามข้างต้นไม่ทับซ้อนซึ่งกันและกัน และยูเนียนของช่วงทั้งหมดเป็นจำนวนจริง

จะได้ว่า f (x) = α_i สำหรับทุกค่าของ x ∈ A_iปริพันธ์เลอเบกของฟังก์ชันขั้นบันได คือ เมื่อ

คือความยาวของช่วง A และในกรณีนี้เราสมมติว่าช่วง A_i ทั้งหมดมีความยาวจำกัด

ข้อเท็จจริงคือความเท่ากันนี้สามารถใช้เป็นขั้นตอนแรกในการหาปริพันธ์เลอเบก

ฟังก์ชันเอกซ์โพเนนเชียล

ฟังก์ชันเอกซ์โพเนนเชียล(Exponential Function)

จากการศึกษาในเรื่องเลขยกกำลัง ซึ่งท้ายที่สุดเราได้สนใจเลขยกกำลังที่มีฐานเป็นจำนวนจริงบวก และเลขชี้กำลังเป็นจำนวนจริงใด ๆ
แต่ได้มีนักคณิตศาสตร์ได้สังเกตเห็นว่า ถ้าเลขยกกำลังมีฐานเป็น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ ดังนี้

ถ้ากำหนดให้ a = 1 และ x เป็นจำนวนจริงใดแล้วจะได้
ax = 1x = 1

ข้อสังเกต

ไม่ว่า x จะเป็นจำนวนจริงใด ๆ ก็ตาม 1x ก็ยังคงเท่ากับ 1 เสมอ ดังนั้นจึงไม่น่าสนใจ เนื่องจาก เราทราบว่ามันเป็นอะไรแน่ ๆ อยู่แล้ว
เรายังไม่ทราบนะว่า เลขยกกำลังที่มีฐานเป็นจำนวนจริงบวกยกเว้น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ แสดงว่าเราจะต้องสนใจศึกษาเลขยกกำลังลักษณะนี้เป็นพิเศษ ซึ่งจะกล่าวถึงใน เรื่องฟังก์ชันเอกซ์โพเนนเชียลดังนี้

ข้อกำหนด (ฟังก์ชันเอกซ์โพเนนเชียล)
ฟังก์ชันเอกซ์โพเนนเชียล คือ f = { (x, y) Î R ´ R+ / y = ax , a > 0, a ¹ 1 }

ข้อตกลง ในหนังสือคณิตศาสตร์บางเล่มให้ข้อกำหนดของฟังก์ชันเอกซ์โพเนนเชียล เป็นฟังก์ชันที่อยู่ในรูป f(x) = kax เมื่อ k เป็นค่าคงตัวที่ไม่ใช่ 0 และ a เป็นจำนวนจริงบวกที่ไม่เป็น 1 แต่ในหลักสูตรมัธยมศึกษาตอนปลายนี้ จะถือว่าฟังก์ชันเอกซ์โพเนนเชียลจะอยู่ในรูป f(x) = ax เมื่อ a เป็น จำนวนจริงบวกที่ไม่เป็น 1 เท่านั้น

ข้อสังเกต จากข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล

f(x) = 1x เป็นฟังก์ชันคงตัวเนื่องจาก 1x = 1 ดังนั้นในข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล จึงไม่สนใจ ฐาน (a) ที่เป็น 1
f(x) = 1x ไม่เป็นฟังก์ชันเอ็กซ์โพเนนเชียล เนื่องจาก f(x) = 1x เป็นฟังก์ชันคงตัว
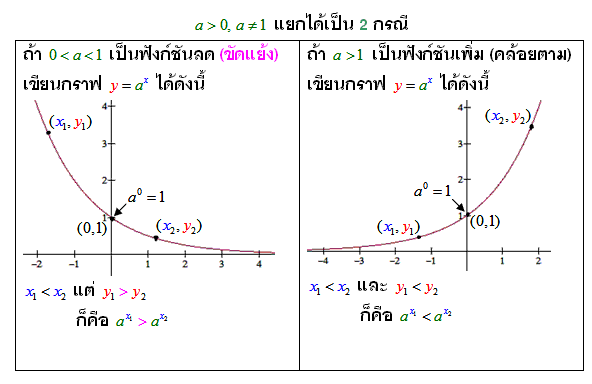
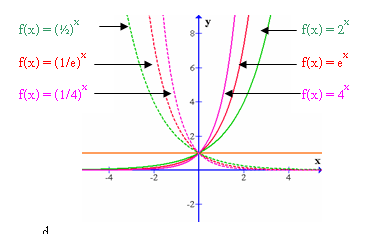
จากเงื่อนไขที่ว่า y = ax, a > 0, a ¹ 1 ทำให้เราทราบได้เลยว่าฐาน (a) มีอยู่ 2 ลักษณะ คือ 0 < a < 1 กับ a > 1
ฟังก์ชันเอกซ์โพเนนเชียลจะมีอยู่ 2 ชนิด โดยขึ้นอยู่กับลักษณะของฐาน (a) ดังนี้

ชนิดที่ 1 y = ax, 0 < a < 1
ชนิดที่ 2 y = ax, a > 1

นิยามของฟังก์ชันเอกซ์โพเนนเชียล

ฟังก์ชันเอกซ์โพเนนเชียล (Exponential Function)

จากการศึกษาในเรื่องเลขยกกำลัง ซึ่งท้ายที่สุดเราได้สนใจเลขยกกำลังที่มีฐานเป็นจำนวนจริงบวก และเลขชี้กำลังเป็นจำนวนจริงใด ๆ

แต่ได้มีนักคณิตศาสตร์ได้สังเกตเห็นว่า ถ้าเลขยกกำลังมีฐานเป็น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ ดังนี้

ถ้ากำหนดให้ a = 1 และ x เป็นจำนวนจริงใดแล้วจะได้

a^x = 1^x = 1

ข้อสังเกต

ไม่ว่า x จะเป็นจำนวนจริงใด ๆ ก็ตาม 1^x ก็ยังคงเท่ากับ 1 เสมอ ดังนั้นจึงไม่น่าสนใจ เนื่องจาก เราทราบว่ามันเป็นอะไรแน่ ๆ อยู่แล้ว
เรายังไม่ทราบนะว่า เลขยกกำลังที่มีฐานเป็นจำนวนจริงบวกยกเว้น 1 และเลขชี้กำลังเป็นจำนวนจริงใด ๆ แสดงว่าเราจะต้องสนใจศึกษาเลขยกกำลังลักษณะนี้เป็นพิเศษ ซึ่งจะกล่าวถึงใน เรื่องฟังก์ชันเอกซ์โพเนนเชียลดังนี้

ข้อกำหนด (ฟังก์ชันเอกซ์โพเนนเชียล)

ฟังก์ชันเอกซ์โพเนนเชียล คือ f = { (x, y) Î R ´ R⁺ / y = a^x , a > 0, a ¹ 1 }

ข้อตกลง ในหนังสือคณิตศาสตร์บางเล่มให้ข้อกำหนดของฟังก์ชันเอกซ์โพเนนเชียล เป็นฟังก์ชันที่อยู่ในรูป f(x) = ka^x เมื่อ k เป็นค่าคงตัวที่ไม่ใช่ 0 และ a เป็นจำนวนจริงบวกที่ไม่เป็น 1 แต่ในหลักสูตรมัธยมศึกษาตอนปลายนี้ จะถือว่าฟังก์ชันเอกซ์โพเนนเชียลจะอยู่ในรูป f(x) = a^x เมื่อ a เป็น จำนวนจริงบวกที่ไม่เป็น 1 เท่านั้น

ข้อสังเกต จากข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล

f(x) = 1^x เป็นฟังก์ชันคงตัวเนื่องจาก 1^x = 1 ดังนั้นในข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียล จึงไม่สนใจ ฐาน (a) ที่เป็น 1
f(x) = 1^x ไม่เป็นฟังก์ชันเอ็กซ์โพเนนเชียล เนื่องจาก f(x) = 1^x เป็นฟังก์ชันคงตัว
จากเงื่อนไขที่ว่า y = a^x, a > 0, a ¹ 1 ทำให้เราทราบได้เลยว่าฐาน (a) มีอยู่ 2 ลักษณะ คือ 0 < a < 1 กับ a > 1
ฟังก์ชันเอกซ์โพเนนเชียลจะมีอยู่ 2 ชนิด โดยขึ้นอยู่กับลักษณะของฐาน (a) ดังนี้

ชนิดที่ 1 y = a^x, 0 < a < 1

ชนิดที่ 2 y = a^x, a > 1

กราฟของฟังก์ชัน y = ax, 0 < a < 1