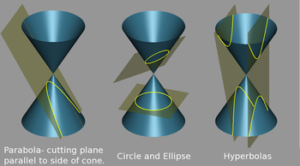
เรียนเลขออนไลน์ ภาคตัดกรวย ม.4

ภาคตัดกรวยจากทางเดินของจุด

แต่ละประเภทของภาคตัดกรวยนั้น สามารถนิยามโดยการใช้เส้นทางเดินของจุด โดยทุก ๆ จุด P บนเส้นทางเดิน จะต้องเป็นไปตามคุณสมบัติเฉพาะดังนี้

วงกลม : ระยะ (P, C) = r โดยที่ C คือจุดตายตัวเรียกว่า จุดศูนย์กลาง และ r คือค่าคงที่ เรียกว่า รัศมี
พาราโบลา : ระยะ (P, F) = ระยะ (P, L) โดยที่ F คือจุดตายตัว เรียกว่า จุดโฟกัส และ L คือ เส้นตรง กำหนดตายตัว และไม่ผ่านจุดโฟกัส เรียกว่า ไดเรกทริกซ์
วงรี : ระยะ (P, A) + ระยะ (P, B) = d โดยที่ A, B เป็นจุดตายตัวสองจุดที่แตกต่างกัน เรียกว่า จุดโฟกัส และ d เป็นค่าคงที่ ที่มีค่ามากกว่า ระยะ(A,B) เรียกว่า เส้นผ่านศูนย์กลางหลัก
ไฮเพอร์โบลา : ระยะ (P, A) – ระยะ (P, B) = d โดยที่ A, B เป็นจุดตายตัวสองจุดที่แตกต่างกัน เรียกว่า จุดโฟกัส และ d เป็นค่าคงที่ ที่มีค่าน้อยกว่า ระยะ (A,B)

ความเยื้อง (ECCENTRICITY)

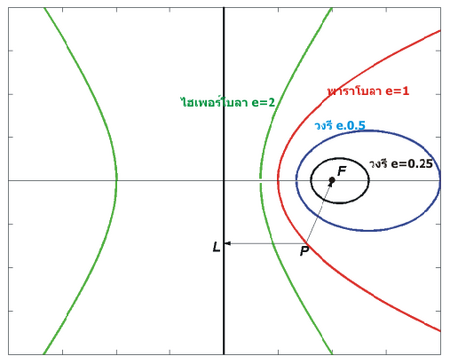
ค่าความเยื้อง หรือ ค่าความเบี่ยงเบนจากศูนย์กลาง (eccentricity) ของภาคตัดกรวย เป็นค่าบ่งชี้ถึงความเบี้ยว หรือ เบี่ยงเบนไปจากความกลม โดยเมื่อความเยื้องมีค่าลดลง รูปร่างของภาคตัดกรวยที่ได้จะมีรูปร่างเข้าใกล้ทรงกลมมากขึ้น

ถ้าเส้นตรง L คือไดเรกทริกซ์ และ F คือ จุดโฟกัส ค่าความเยื้อง e หาได้จาก

$\frac{dist(P,F)}{dist(P,L)} = e \qquad e \in\mathbb{R}^*_+$

โดยที่

$\,dist(P,F)$ คือ ระยะทางจากจุด P ใดๆ บนภาคตัดกรวย ไปยังจุดโฟกัส F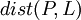
$\,dist(P,L)$ คือ ระยะทางจากจุด P ใดๆ บนภาคตัดกรวย ไปตั้งฉากกับไดเรกทริกซ์ L

รูปร่างของภาคตัดกรวยที่ได้ ขึ้นกับค่า e โดย

0 < e < 1เป็นรูปวงรี
e = 1 เป็นรูปพาราโบลา
e > 1 เป็นรูปไฮเพอร์โบลา

ภาคตัดกรวยกับเรขาคณิตวิเคราะห์

รูปแสดงการตัดกรวยด้วยระนาดในแนวต่าง ๆ

บนระบบพิกัดคาร์ทีเซียน กราฟของสมการสองตัวแปรกำลังสอง (quadratic equation) จะเป็นรูปภาคตัดกรวยเสมอ หากเราพิจารณาสมการที่อยู่ในรูป

แล้ว:

ถ้า h² = ab แล้ว จะได้สมการของรูป พาราโบลา
ถ้า h² < ab และ a $\ne$ b และ/หรือ h $\ne$ 0 แล้ว จะได้สมการของรูป วงรี
ถ้า h² > ab แล้ว จะได้สมการของรูป ไฮเพอร์โบลา
ถ้า h² < ab and a = b and h = 0 แล้ว จะได้สมการของรูป วงกลม
ถ้า a + b = 0 แล้ว จะได้สมการของรูป ไฮเพอร์โบลามุมฉาก

สมบัติทั่วไป

ภาคตัดกรวยนั้นมีรูปร่างที่มนสม่ำเสมอ ไม่มีจุดเปลี่ยนโค้ง (inflection point) ซึ่งเป็นสมบัติที่มีความสำคัญต่อการใช้งานหลายประเภท เช่น การใช้งานเกี่ยวกับแอโรไดนามิกส์ ซึ่งพื้นผิวนั้นจำเป็นต้องออกแบบเพื่อให้ของไหล ไหลผ่านอย่างสม่ำเสมอ (laminar flow) เพื่อป้องกันการเกิดการไหลทะลัก (turbulence)

การประยุกต์ใช้งาน

ภาคตัดกรวยนั้นได้มีความสำคัญต่อดาราศาสตร์ โดย วงโคจรของวัตถุสองชิ้นซึ่งมีแรงดึงดูดกระทำต่อกัน ตามกฏของนิวตัน นั้นจะมีรูปร่างเป็นภาคตัดกรวย หากจุดศูนย์กลางมวล (center of mass) ร่วมของทั้งสองวัตถุนั้นอยู่นิ่ง หากทั้งสองนั้นถูกดึงดูดอยู่ด้วยกัน ทางเดินของทั้งสองนั้นจะเป็นรูปวงรี หากวัตถุทั้งสองวิ่งออกจากกัน ทางเดินจะเป็นรูปพาราโบลา หรือ ไฮเปอร์โบลา ดู ปัญหาวัตถุ N ชิ้น

ในเรขาคณิตเชิงภาพฉาย (projective geometry) นั้น ภาพฉายบนระนาบ ของภาคตัดกรวยแต่ละชนิดนั้นจะเหมือนกัน ขึ้นอยู่กับลักษณะการฉาย หรือที่เรียกว่า การแปลงเชิงภาพฉาย (projective transformation)

มีคำศัพท์ที่กล่าวถึงส่วนประกอบต่างๆ ของภาคตัดกรวย ดังนี้

สมการวงกลม

วงกลม คือเซตของจุดทุกจุดซึ่งห่างจากจุดคงที่จุดหนึ่งเป็นระยะทางคงตัว จุดคงที่ เรียกว่า จุดศูนย์กลาง ส่วนระยะคงที่เรียกว่า รัศมี

นิยามของสมการวงกลมคือ

วงกลม (circle) คือเซตของจุดทั้งหมดในระนาบที่ห่างจากจุดๆหนึ่งตรึงอยู่กับที่เป็นระยะทางคงตัว จุดที่ตรึงอยู่กับที่นี้เรียกว่า จุดศูนย์กลาง (center) ของวงกลม และระยะทางคงตัวดังกล่าวเรียกว่า รัศมี (radius) ของวงกลม

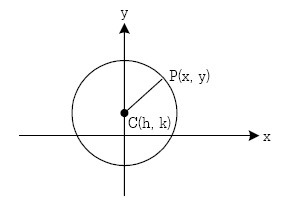
จุด C(h,k) เป็นจุดคงที่ เรียกว่า จุดศูนย์กลาง

|CP| = ระยะทางคงที่ เรียกว่ารัศมี

ถ้า D² + E² – 4F = 0 กราฟที่ได้จะเป็นจุดวงกลม
ถ้า D² + E² – 4F > 0 กราฟที่ได้จึงเป็นวงกลม
ถ้า D² + E² – 4F < 0 จะไม่เกิดกราฟในระบบจำนวนจริงถ้าต้องการหาสมการวงกลม จะต้องทราบ
1. จุดศูนย์กลาง
2. รัศมี.