เรื่องทฤษฎีบทพีทาโกรัส เรียนเรื่องอะไรบ้าง

เรื่องทฤษฎีบทพีทาโกรัส เรียนเรื่องอะไรบ้าง

สรุปทฤษฎีพีทากอรัส

ในสามเหลี่ยมมุมฉากใดๆ พื้นที่ของสี่เหลี่ยมจตุรัสที่มีด้านเป็นด้านตรงข้ามมุมฉาก จะเท่ากับผลรวมของสี่เหลี่ยมจตุรัสที่มีด้านเป็นด้านประชิดมุมฉากของสามเหลี่ยมมุมฉากนั้น ดังนั้นจะได้สูตร c² = a² + b²

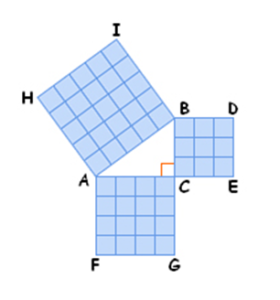
a แทน ความยาวตรงข้ามมุม A

b แทน ความยาวตรงข้ามมุม B

c แทน ความยาวตรงข้ามมุม C

ด้าน AB เรียกว่า ด้านตรงข้ามมุมฉาก

ด้าน AC และ BC เรียกว่า ด้านประกอบมุมฉาก

บทกลับทฤษฎีบทพีทาโกรัส

c² = a² + b² สามเหลี่ยมที่ได้จะเป็นสามเหลี่ยมมุมฉาก

c² > a² + b² สามเหลี่ยมที่ได้จะเป็นสามเหลี่ยมมุมป้าน

c² < a² + b² สามเหลี่ยมที่ได้จะเป็นสามเหลี่ยมมุมแหลม

Euclid’s Elements ของ ยุคลิดด้วย โดยบทกลับนี้สามารถพิสูจน์ได้โดยใช้ กฎของโคไซน์ หรือตามการพิสูจน์ดังต่อไปนี้

“กำหนดสามเหลี่ยม ABC มีด้านสามด้านที่มีความยาว a,b และ c และ a² + b² = c² เราจะต้องพิสูจน์ว่ามุมระหว่าง a และ b เป็นมุมฉาก ดังนั้น เราจะสร้างสามเหลื่ยมมุมฉากที่มีความยาวของด้านประกอบมุมฉาก เป็น a และ b แต่จากทฤษฎีบทปีทาโกรัส เราจะได้ว่าด้านตรงข้ามมุมฉาก ของสามเหลื่ยมรูปที่สองก็จะมีค่าเท่ากับ c เนื่องจากสามเหลี่ยมทั้งสองรูปมีความยาวด้านเท่ากันทุกด้าน สามเหลี่ยมทั้งสองรูปจึงเท่ากันทุกประการแบบ “ด้าน-ด้าน-ด้าน” และต้องมีมุมขนาดเท่ากันทุกมุม ดังนั้นมุมที่ด้าน a และ b มาประกอบกัน จึงต้องเป็นมุมฉากด้วย”

ตัวอย่าง

กำหนดความยาวของด้านสามด้าน ได้แก่ด้าน a = 4, b = 5 และ c = 6  นำทั้งสามด้านมาสร้างเป็นรูปสามเหลี่ยม จะได้รูปสามเหลี่ยมอะไร

เป็นอย่างไรกันบ้างคะ สำหรับทฤษฎีบทพีทาโกรัส