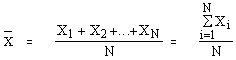เรื่องสถิติ เรียนอะไรบ้าง ออนไลน์คณิตศาสตร์ม.2
สถิติคือตัวเลขที่ใช้บรรยายเหตุการณ์หรือข้อเท็จจริง มานำเสนอในรูปแบบต่างๆ
แผนภาพจุด เป็นการนำเสนอข้อมูลเชิงปริมาตร โดยการเขียนจุดแทนข้อมูลแต่ละตัวไว้เหนือเส้นในแนวนอน
แผนภาพต้นใบ เป็นการนำเสนอข้อมูลเชิงปริมาณ มีสองส่วน คือ ส่วนใบอยู่ขวา ส่วนลำต้นอยู่ทางซ้าย
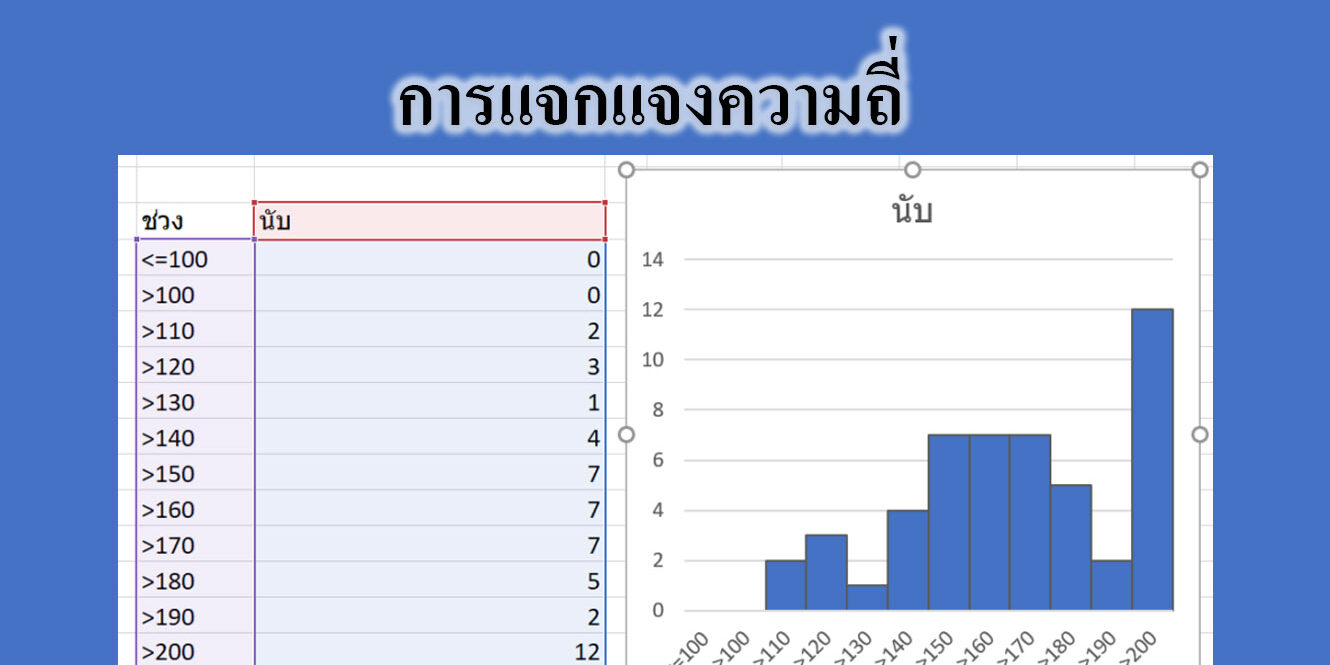
ฮิสโทแกรม ใช้สำหรับการกระจายของข้อมูลจำนวนมากๆ ลักษณะคล้ายกับแผนภูมิแท่ง
พิสัย คือ ค่าสูงสุด – ค่าต่ำสุดของข้อมูล
ค่ากลางของข้อมูลมีสามอย่าง ได้แก่ ค่าเฉลี่ย มัธยฐาน และฐานนิยม
ค่าเฉลี่ยเลขคณิต คือ จำนวนที่ได้จากการหารผลบวกของข้อมูลทั้งหมดด้วยจำนวนข้อมูล
ค่ามัธยฐาน คือ หาค่าที่อยู่ตรงกลาง เมื่อนำข้อมูลมาเรียงจากน้อยไปหามาก หรือมากไปหาน้อยแล้ว
ฐานนิยม คือ ข้อมูลที่มีความถี่สูงสุดในชุดนั้นๆ (ซ้ำกันมากที่สุด)
การวัดค่ากลางของข้อมูล
1. ค่าเฉลี่ยเลขคณิต (Mean) คือ ผลรวมของค่าของข้อมูลทั้งหมด หารด้วยจำนวนของข้อมูล
การวัดค่ากลางของข้อมูล
การวัดค่ากลางของข้อมูล
การหาค่ากลางของข้อมูลที่เป็นตัวแทนของข้อมูลทั้งหมดเพื่อความสะดวกในการสรุปเรื่องราวเกี่ยวกับข้อมูลนั้นๆ จะช่วยทำให้เกิดการวิเคราะห์ข้อมูลถูกต้องดีขึ้น การหาค่ากลางของข้อมูลมีวิธีหาหลายวิธี แต่ละวิธีมีข้อดีและข้อเสีย และมีความเหมาะสมในการนำไปใช้ไม่เหมือนกัน ขึ้นอยู่กับลักษณะข้อมูลและวัตถุประสงค์ของผู้ใช้ข้อมูลนั้นๆ
ค่ากลางของข้อมูลที่สำคัญ มี 3 ชนิด คือ
1. ค่าเฉลี่ยเลขคณิต (Arithmetic mean)
2. มัธยฐาน (Median)
3. ฐานนิยม (Mode)
1. ค่าเฉลี่ยเลขคณิต (Arithmetic mean)
ใช้สัญลักษณ์ คือ
1.1 การหาค่าเฉลี่ยเลขคณิตของข้อมูลที่ไม่แจกแจงความถี่
ให้ x 1 , x 2 , x 3 , …, x N เป็นข้อมูล N ค่า x̄
ค่าเฉลี่ยเลขคณิต (arithmetic mean)
หมายถึง การหารผลรวมของข้อมูลทั้งหมดด้วยจำนวนข้อมูลทั้งหมด การหาค่าเฉลี่ยเลขคณิตสามารถหาได้ 2 วิธี
1. ค่าเฉลียเลขคณิตของข้อมูลที่ไม่ได้แจกแจงความถี่ สามารถคำนวณได้จากสูตร
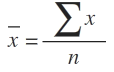
ค่าเฉลี่ยเลขคณิต หรือที่เราเรียกกันย่อๆ ว่าค่าเฉลี่ย เขียนแทนด้วยสัญลักษณ์ (x¯) เป็นค่ากลางทางสถิติค่าหนึ่ง ที่เจอบ่อยและใช้กันเยอะมาก
วิธีการหาค่าเฉลี่ยเลขคณิตของข้อมูลแบบไม่แจกแจงความถี่สามารถทำได้ดังนี้

ตัวอย่าง 1 ) หาค่าเฉลี่ยจากข้อมูลชุดนี้ 1,2,2,5,7,11,15,9
วิธีทำ

ตอบ 6.5
คุณสมบัติบางประการของมัชฌิมเลขคณิต
มัชฌิมเลขคณิตมีคุณสมบัติบางประการดังนี้ประการแรก คุณสมบัติพื้นฐานก็คือ ผลบวกของความเบี่ยงเบนของคะแนนดิบกับคะแนนเฉลี่ยมีค่าเป็น 0ค่ามัชฌิมเลขคณิตของคะแนน 7, 13, 22, 9, 11 และ 4 คือ 11 ส่วนเบี่ยงเบนจากคะแนนเฉลี่ยคือ -4, 2, 11, -2, 0 และ -7 ผลบวกของคะแนนเบี่ยงเบนคือ 0 ผลทั้งหมดเขียนเป็นสัญลักษณ์ได้ดังนี้
![]()
ประการสอง ผลรวมของกำลังสองของคะแนนเบี่ยงเบนจะมีค่าน้อยที่สุดความเบี่ยงเบนของค่าที่ได้จากการวัด 7, 13, 22, 9, 11, 4 กับค่าเฉลี่ย 11 คือ -4, 2, 11, -2, 0, -7 ค่ากำลังสองของความเบี่ยงเบนจะได้ 16, 4, 121, 4, 0, 49 ผลบวกของกำลังสองเท่ากับ 197 ถ้าหากเราใช้ค่าเฉลี่ยตัวอื่น ๆ ผลบวกของกำลังสองของความเบี่ยงเบนของค่าการวัดกับค่ากึ่งกลางใด ๆ จะได้ค่าสูงกว่าผลรวมของกำลังสองความเบี่ยงเบนของค่าการวัดกับมัชฌิมเลขคณิต สมมติให้ค่ากึ่งกลางของข้อมูลชุดนี้เป็น 13 ความเบี่ยงเบนจะได้ -6, 0, 9, 4, 2, -9 ยกกำลังสองได้ 36, 0, 81, 16, 4, 81 รวมผลทั้งหมดเท่ากับ 218 ซึ่งมากกว่าค่าที่ได้จากการใช้ค่าเฉลี่ย
ข้อดีข้อเสียของมัชฌิมเลขคณิต
ข้อดี
1. คำนวณได้ง่าย
2. ข้อมูลทุกตัวถูกนำมาใช้ในการคำนวณ
3. สามารถนำค่าเฉลี่ยที่ได้มาใช้ในการคำนวณอื่น ๆ
ข้อเสีย
1. เพราะข้อมูลทุกค่าถูกนำมาใช้ในการคำนวณ ถ้ามีข้อมูลบางค่าผิดปกติค่าเฉลี่ยก็จะผิดปกติไปด้วย
2. ในกรณีที่อันตรภาคชั้นแต่ละชั้นเป็นชั้นเปิด ไม่สามารถหามัชฌิมเลขคณิตได้
มัธยฐาน (Median)
มัธยฐาน หมายถึงค่าที่อยู่ในตำแหน่งกึ่งกลางของข้อมูลชุดนั้น เมื่อได้จากเรียงค่าของข้อมูลจากน้อยที่ไปหามากที่สุดไปหาน้อยที่สุด ค่ากึ่งกลางจะเป็นตัวแทนที่แสดงว่ามีข้อมูลที่มากกว่าและน้อยกว่านี้อยู่ 50 เปอร์เซนต์
การหาค่ามัธยฐานของข้อมูลที่ไม่ได้จัดหมวดหมู่(Ungrouped Data)
ให้เรียงข้อมูลที่มีค่าน้อยที่สุดไปหาข้อมูลที่มีค่ามากที่สุดหรือจากมากสุดไปหาน้อยที่สุดแล้วหาคะแนนที่อยู่ในตำแหน่งกึ่งกลาง
จงหามัธยฐานของข้อมูลต่อไปนี้ 9,5,11,16,6,10,13,14,3
วิธีทำ เรียงข้อมูลที่มีค่าน้อยที่สุดไปหาข้อมูลที่มีค่ามากที่สุดคือ
3,5,6,9,10,11,13,14,16
Median จะอยู่ตำแหน่งที่ N+1 = 9+1
2 2 = 5
ดังนั้น ค่ามัธฐานเท่ากับ 10
ขั้นตอนการสร้างตารางแจกแจงความถี่
การสร้างตารางแจกแจงความถี่มีขั้นตอน ดังนี้
1). หาค่าพิสัยของข้อมูลโดยที่ค่าพิสัย(Range)คือผลต่างระหว่างข้อมูลที่มีค่ามากที่สุดกับข้อมูลที่มีค่าน้อยที่สุดดังนั้น
|
พิสัย = ค่าสูงสุด – ค่าต่ำสุด |
ถ้ามีข้อมูล N ค่า คือ X1 ,X2,…XNและให้ Xmax = ค่าสูงสุดของข้อมูล = max(X1 ,X2,…XN)
Xmin = ค่าต่ำสุดของข้อมูล = min (X1 ,X2,…XN)
ดังนั้น พิสัย = R = Xmax – Xmin
2)กำหมดจำนวนชั้น (k)
โดยกำนดจำนวนชั้นเป็น 5-20 ชั้น ถ้าข้อมูลมีการกระจายมากและมีจำนวนข้อมูลไม่มากควรให้มีจำนวนชั้นน้อยๆ เพื่อป้องกันไม่ให้มีชั้นที่มีชั้นที่มีค่าความถี่เป็นศูนย์ เนื่องจากไม่มีข้อมูลค่าใดที่ตกอยู่ในชั้นๆเลยในกรณีนี้ที่สร้างไม่ทราบว่าควรกำหมดให้ตารางแจกแจงความถี่มีกั่ชั้นส่ามารถใช้สูตรในการคำนวณชั้นได้ ด้งนี้
| K = 1+ 3.3 log N |
|
I = ความกว้างของชั้น (อันตรภาคชั้น) = พิสัย
จำนวนชั้น =R/k
|
ถ้าค่า I เป็นเลขไม่ลงตัว จะปัดให้เป็นจำนวนเต็ม(ไม่ว่าเศษจะมีค่าต่ำกว่าหรือมากกว่า 0.5)โดยทั่วไปมักกำหมดให้ความกว้างของแต่ละชั้นเท่ากันหมด แต่ละในทางปฏิบัติบางครั้งอาจจะให้ความกว้างของแต่ละชั้นไม่เท่ากัน หรืออาจกำหมดให้เป็นชั้นเปืดก็ได้หรืออาจจะกำหมดให้ความกว้างของชั้นเป็นค่าที่ทำให้ค่ากึ่งกลางชั้น มีค่าเท่ากับจริงของข้อมูล
| ค่ากึ่งกลางชั้น = (ขอบเขตกำจัดบน + ขอบเขตจำกัดล่าง )/2 = (ขีดจำกัดบน + ขีดจำกัดล่าง )/2 |
โดยจะกำหมดให้ขีดจำกัดล่างของชั้นแรก (ชั้นที่มีค่าต่ำสุด) ครอบคลุมข้อมูลที่มีค่าต่ำสุดและให้ขีดจำกัดบนของชั้นสุดท้าย (ชั้นที่มีค่าสูงสุด)ครอบคลุมข้อมูลที่มีค่าสูงสุด หรืออาจใช้สูตรต่อไปนี้
| ขีดจำกัดล่างของชั้นแรก = ค่าต่ำ – (Ik – R)/2 |
5).คำนวณหาขอบเขตจำกัดชั้น (Class Boundaries)
การหาขอบเขตชั้นนั้นจะกำหนดให้ขอบเขตชั้นมีจำนวนหลักหลังจุดทศนิยมมากกว่าของข้อมูลจริงอยู่ 1 หลักเสมอ เช่น ถ้าข้อมูลจริงเป็นเลขจำนวนเต็ม ขอลเขตจำกัดชั้นจะมีจำนวนจุดทศนิยม 1 หลัก ในทางปฏิบัติ เราสามารถหาค่าขอบเขตชั้นได้ ดังนี้
| ขอบเขตจำกัดชั้นื = (ขีดจำกัดบนของชั้น + ขีดจำกัดล่างของชั้นถัดไป)/2 |
6). นับจำนวนค่าของข้อมูล (ความถี่) ในแต่ละชั้น
หลังจากสร้างขอบเขตจำกัดชั้นแล้ว จึงตรวจสอบว่าข้อมูลค่าใดอยู่ในชั้นได้บ้าง แล้วนับจำนวนข้อมูลในแต่ละชั้นเรียกว่า ความถี่ของชั้น